Ósmy wyraz ciągu 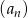 o wyrazie ogólnym
o wyrazie ogólnym 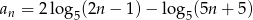 , gdzie
, gdzie 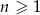 jest równy
jest równy
A) 1 B) 5 C) -1 D) -5
/Szkoła średnia/Zadania testowe
Siódmy wyraz ciągu 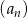 o wyrazie ogólnym
o wyrazie ogólnym 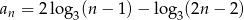 , gdzie
, gdzie 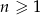 jest równy
jest równy
A) 1 B) 2 C) -1 D) -2
Dany jest okrąg o środku w punkcie 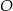 . Prosta
. Prosta 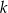 jest styczna do okręgu w punkcie
jest styczna do okręgu w punkcie 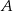 .
.
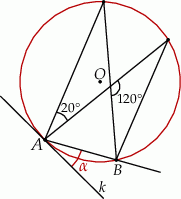
Miara kąta  jest równa
jest równa
A) 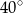 B)
B) 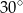 C)
C) 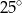 D)
D) 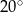
Dany jest okrąg o środku w punkcie 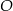 . Prosta
. Prosta 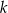 jest styczna do okręgu w punkcie
jest styczna do okręgu w punkcie 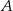 .
.
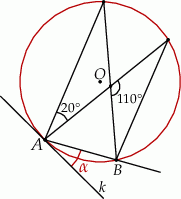
Miara kąta  jest równa
jest równa
A) 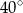 B)
B) 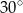 C)
C) 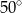 D)
D) 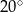
Przeciwległe wierzchołki kwadratu mają współrzędne 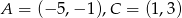 . Promień okręgu wpisanego w ten kwadrat jest równy
. Promień okręgu wpisanego w ten kwadrat jest równy
A) 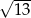 B)
B) 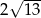 C)
C) 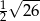 D)
D) 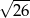
Przeciwległe wierzchołki kwadratu mają współrzędne 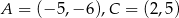 . Promień okręgu wpisanego w ten kwadrat jest równy
. Promień okręgu wpisanego w ten kwadrat jest równy
A) 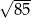 B)
B) 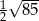 C)
C) 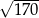 D)
D) 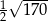
Przeciwległe wierzchołki kwadratu mają współrzędne 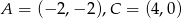 . Promień okręgu wpisanego w ten kwadrat jest równy
. Promień okręgu wpisanego w ten kwadrat jest równy
A) 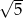 B)
B) 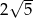 C)
C) 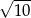 D)
D) 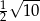
Przeciwległe wierzchołki kwadratu mają współrzędne 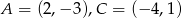 . Średnica okręgu wpisanego w ten kwadrat jest równa
. Średnica okręgu wpisanego w ten kwadrat jest równa
A) 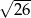 B)
B) 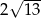 C)
C) 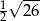 D)
D) 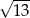
Kąt  jest ostry i
jest ostry i 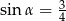 . Wartość wyrażenia
. Wartość wyrażenia 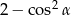 jest równa
jest równa
A) 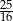 B)
B)  C)
C) 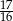 D)
D) 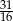
Kąt  jest ostry i
jest ostry i 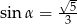 . Wartość wyrażenia
. Wartość wyrażenia 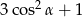 jest równa
jest równa
A)  B)
B) 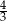 C)
C)  D)
D) 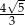
Kąt  jest ostry i
jest ostry i 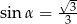 . Wtedy wartość wyrażenia
. Wtedy wartość wyrażenia 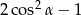 jest równa
jest równa
A) 0 B) 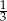 C)
C) 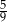 D) 1
D) 1
Kąt  jest ostry i
jest ostry i 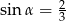 . Wartość wyrażenia
. Wartość wyrażenia 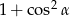 jest równa
jest równa
A) 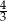 B)
B) 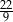 C)
C) 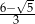 D)
D) 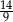
Kąt  jest ostry i
jest ostry i 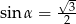 . Wartość wyrażenia
. Wartość wyrażenia 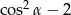 jest równa
jest równa
A) 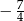 B)
B) 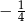 C)
C) 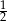 D)
D) 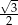
Z prostokąta 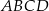 o polu 30 wycięto trójkąt
o polu 30 wycięto trójkąt 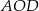 (tak jak na rysunku). Pole zacieniowanej figury jest równe
(tak jak na rysunku). Pole zacieniowanej figury jest równe
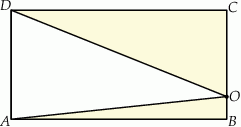
A) 7,5 B) 15 C) 20 D) 25
Z prostokąta 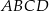 o polu 28 wycięto trójkąt
o polu 28 wycięto trójkąt 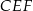 , przy czym punkty
, przy czym punkty 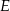 i
i 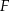 są środkami odpowiednio boków
są środkami odpowiednio boków 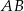 i
i  .
.
Pole zacieniowanej figury jest równe
A) 3,5 B) 21 C) 25 D) 24,5
Prawdopodobieństwo zdarzenia 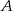 jest 6 razy mniejsze niż prawdopodobieństwo zdarzenia przeciwnego do
jest 6 razy mniejsze niż prawdopodobieństwo zdarzenia przeciwnego do 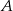 . Wobec tego prawdopodobieństwo zdarzenia
. Wobec tego prawdopodobieństwo zdarzenia 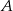 jest równe
jest równe
A) 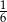 B)
B)  C)
C) 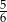 D)
D) 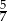
Jeżeli prawdopodobieństwo zdarzenia losowego 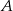 jest 5 razy większe od prawdopodobieństwa zdarzenia przeciwnego do zdarzenia
jest 5 razy większe od prawdopodobieństwa zdarzenia przeciwnego do zdarzenia 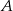 , to prawdopodobieństwo zdarzenia
, to prawdopodobieństwo zdarzenia 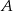 jest równe
jest równe
A) 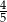 B)
B) 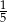 C)
C) 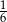 D)
D) 
Prawdopodobieństwo zdarzenia 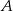 jest 6 razy większe niż prawdopodobieństwo zdarzenia przeciwnego do
jest 6 razy większe niż prawdopodobieństwo zdarzenia przeciwnego do 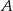 . Wobec tego prawdopodobieństwo zdarzenia
. Wobec tego prawdopodobieństwo zdarzenia 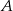 jest równe
jest równe
A) 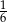 B)
B)  C)
C) 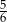 D)
D) 
Prawdopodobieństwo zdarzenia 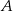 jest 5 razy mniejsze niż prawdopodobieństwo zdarzenia przeciwnego do
jest 5 razy mniejsze niż prawdopodobieństwo zdarzenia przeciwnego do 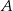 . Wobec tego prawdopodobieństwo zdarzenia
. Wobec tego prawdopodobieństwo zdarzenia 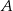 jest równe
jest równe
A)  B)
B) 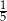 C)
C)  D)
D) 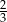
Jeżeli 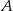 jest zdarzeniem losowym, a
jest zdarzeniem losowym, a 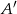 – zdarzeniem przeciwnym do zdarzenia
– zdarzeniem przeciwnym do zdarzenia 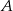 oraz zachodzi równość
oraz zachodzi równość 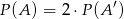 , to
, to
A) 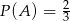 B)
B) 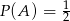 C)
C) 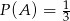 D)
D) 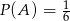
Jeżeli 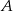 jest zdarzeniem losowym oraz
jest zdarzeniem losowym oraz 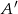 jest zdarzeniem przeciwnym do zdarzenia
jest zdarzeniem przeciwnym do zdarzenia 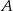 i
i 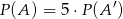 , to prawdopodobieństwo zdarzenia
, to prawdopodobieństwo zdarzenia 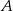 jest równe
jest równe
A) 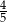 B)
B) 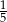 C)
C) 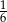 D)
D) 
Prawdopodobieństwo zdarzenia 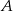 jest 7 razy większe niż prawdopodobieństwo zdarzenia przeciwnego do
jest 7 razy większe niż prawdopodobieństwo zdarzenia przeciwnego do 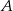 . Wobec tego prawdopodobieństwo zdarzenia
. Wobec tego prawdopodobieństwo zdarzenia 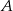 jest równe
jest równe
A)  B)
B)  C)
C) 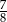 D)
D) 
Prawdopodobieństwo zdarzenia 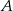 jest 3 razy mniejsze niż prawdopodobieństwo zdarzenia przeciwnego do
jest 3 razy mniejsze niż prawdopodobieństwo zdarzenia przeciwnego do 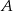 . Wobec tego prawdopodobieństwo zdarzenia
. Wobec tego prawdopodobieństwo zdarzenia 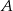 jest równe
jest równe
A) 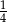 B)
B) 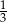 C)
C) 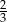 D)
D) 
Wartość wyrażenia 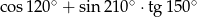 jest równa
jest równa
A) 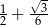 B)
B) 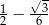 C)
C) 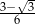 D)
D) 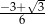
Wartość wyrażenia 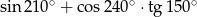 jest równa
jest równa
A) 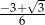 B)
B) 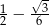 C)
C) 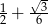 D)
D) 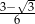
W ciągu arytmetycznym 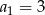 oraz
oraz 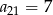 . Wtedy suma
. Wtedy suma 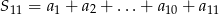 jest równa
jest równa
A) 44 B) 88 C) 46 D) 55
Z trójkąta 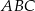 o obwodzie 50 wycięto kwadrat
o obwodzie 50 wycięto kwadrat 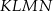 o obwodzie 20 (tak jak na rysunku). Obwód zacieniowanej figury jest równy
o obwodzie 20 (tak jak na rysunku). Obwód zacieniowanej figury jest równy
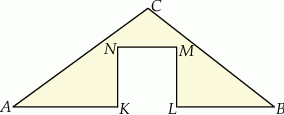
A) 64 B) 60 C) 75 D) 70
Doświadczenie losowe polega na czterokrotnym rzucie symetryczną sześcienną kostką do gry, która na każdej ściance ma inną liczbę oczek – od jednego oczka do sześciu oczek. Prawdopodobieństwo zdarzenia polegającego na tym, że iloczyn liczb wyrzuconych oczek jest liczbą nieparzystą, jest równe
A) 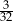 B)
B) 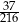 C)
C) 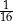 D)
D) 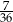
W kartezjańskim układzie współrzędnych 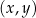 dana jest prosta
dana jest prosta 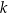 o równaniu
o równaniu 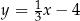 . Prosta o równaniu
. Prosta o równaniu 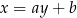 jest równoległa do prostej
jest równoległa do prostej 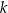 i przechodzi przez punkt
i przechodzi przez punkt 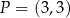 , gdy
, gdy
A) 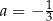 i
i 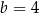 B)
B) 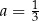 i
i 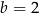 C)
C) 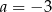 i
i 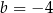 D)
D) 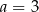 i
i 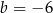
Miejsce zerowe funkcji liniowej 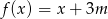 jest większe od 2 dla każdej liczby
jest większe od 2 dla każdej liczby 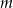 spełniającej warunek
spełniającej warunek
A) 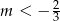 B)
B) 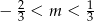 C)
C) 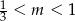 D)
D) 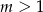
Dla każdej dodatniej liczby  wyrażenie
wyrażenie 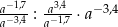 jest równe
jest równe
A) 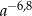 B)
B) 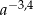 C) 1 D)
C) 1 D) 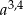
Wyrażenie 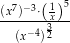 jest równe
jest równe
A) 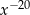 B)
B) 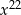 C)
C) 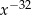 D)
D) 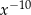
Powierzchnia boczna walca o objętości 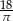 po rozwinięciu jest prostokątem, w którym przekątna tworzy z wysokością walca kąt o mierze
po rozwinięciu jest prostokątem, w którym przekątna tworzy z wysokością walca kąt o mierze 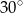 . Promień podstawy tego walca jest równy
. Promień podstawy tego walca jest równy
A) 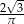 B)
B) 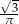 C)
C) 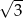 D)
D) 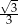
Krawędź podstawy ostrosłupa prawidłowego czworokątnego jest dwa razy dłuższa od jego wysokości. Kąt nachylenia ściany bocznej do podstawy ma miarę
A) 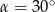 B)
B) 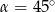 C)
C) 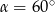 D)
D) 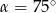
W ciągu geometrycznym pierwszy wyraz 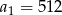 , a iloraz
, a iloraz 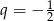 . Ósmy wyraz tego ciągu jest równy
. Ósmy wyraz tego ciągu jest równy
A) -4 B) -2 C) 2 D) 4
Dany jest ciąg geometryczny 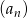 , w którym
, w którym 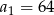 i
i 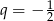 . Wówczas
. Wówczas
A) 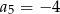 B)
B) 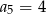 C)
C) 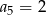 D)
D) 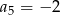
W ciągu geometrycznym pierwszy wyraz 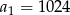 , a iloraz
, a iloraz 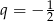 . Dziewiąty wyraz tego ciągu jest równy
. Dziewiąty wyraz tego ciągu jest równy
A) -2 B) -4 C) 4 D) 2
W ciągu geometrycznym pierwszy wyraz 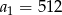 , a iloraz
, a iloraz 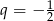 . Siódmy wyraz tego ciągu jest równy
. Siódmy wyraz tego ciągu jest równy
A) -8 B) -4 C) 4 D) 8
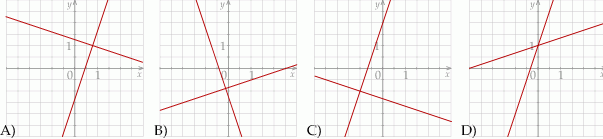
Dany jest układ równań
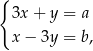
gdzie  i
i 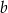 są pewnymi liczbami rzeczywistymi. Na którym z rysunków może być przedstawiona interpretacja geometryczna tego układu równań?
są pewnymi liczbami rzeczywistymi. Na którym z rysunków może być przedstawiona interpretacja geometryczna tego układu równań?
Jacek bierze udział w olimpiadzie chemicznej i olimpiadzie matematycznej. Prawdopodobieństwo, że zostanie laureatem olimpiady chemicznej jest równe 0,3, a prawdopodobieństwo, że zostanie laureatem przynajmniej jednej z tych dwóch olimpiad wynosi 0,72. Prawdopodobieństwo, że będzie laureatem obu olimpiad jest równe 0,18. Zatem prawdopodobieństwo, że będzie laureatem olimpiady matematycznej jest równe
A) 0,1 B) 0,6 C) 0,7 D) 0,4
Ania bierze udział w olimpiadzie biologicznej i olimpiadzie fizycznej. Prawdopodobieństwo, że zostanie laureatką olimpiady biologicznej jest równe 0,4, a prawdopodobieństwo, że zostanie laureatką przynajmniej jednej z tych dwóch olimpiad wynosi 0,62. Prawdopodobieństwo, że będzie laureatką obu olimpiad jest równe 0,18. Zatem prawdopodobieństwo, że będzie laureatką olimpiady fizycznej jest równe
A) 0,4 B) 0,3 C) 0,5 D) 0,2
Tomek bierze udział w olimpiadzie fizycznej i olimpiadzie matematycznej. Prawdopodobieństwo, że zostanie laureatem olimpiady fizycznej jest równe 0,5, a prawdopodobieństwo, że zostanie laureatem przynajmniej jednej z tych dwóch olimpiad wynosi 0,74. Prawdopodobieństwo, że będzie laureatem obu olimpiad jest równe 0,26. Zatem prawdopodobieństwo, że będzie laureatem olimpiady matematycznej jest równe
A) 0,5 B) 0,6 C) 0,7 D) 0,4
Zbiorem rozwiązań nierówności 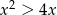 jest
jest
A) 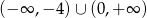 B)
B) 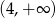 C)
C) 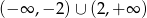 D)
D) 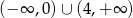
Rozwiązaniem nierówności 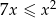 jest zbiór
jest zbiór
A) 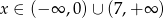 B)
B) 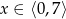 C)
C) 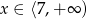 D)
D) 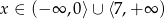
Zbiorem rozwiązań nierówności 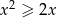 jest:
jest:
A) 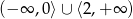 B)
B) 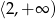 C)
C) 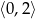 D)
D) 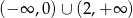
Zbiorem rozwiązań nierówności 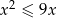 jest przedział
jest przedział
A) 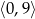 B)
B) 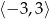 C)
C) 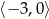 D)
D) 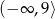
Zbiorem rozwiązań nierówności 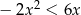 jest
jest
A) 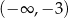 B)
B) 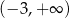 C)
C) 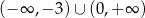 D)
D) 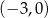
Kąt środkowy i kąt wpisany są oparte na tym samym łuku. Suma ich miar jest równa 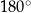 . Jaka jest miara kąta środkowego?
. Jaka jest miara kąta środkowego?
A) 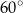 B)
B) 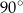 C)
C) 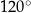 D)
D) 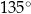
Miara kąta wpisanego w okrąg jest o 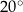 mniejsza od miary kąta środkowego opartego na tym samym łuku. Wynika stąd, że miara kąta wpisanego jest równa
mniejsza od miary kąta środkowego opartego na tym samym łuku. Wynika stąd, że miara kąta wpisanego jest równa
A) 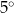 B)
B) 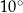 C)
C) 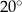 D)
D) 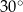
Miara kąta wpisanego w okrąg jest o 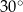 mniejsza od miary kąta środkowego opartego na tym samym łuku. Wynika stąd, że miara kąta wpisanego jest równa
mniejsza od miary kąta środkowego opartego na tym samym łuku. Wynika stąd, że miara kąta wpisanego jest równa
A) 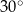 B)
B) 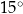 C)
C) 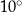 D)
D) 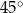
Kąt środkowy i kąt wpisany są oparte na tym samym łuku. Suma ich miar jest równa 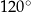 . Jaka jest miara kąta środkowego?
. Jaka jest miara kąta środkowego?
A) 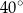 B)
B) 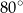 C)
C) 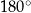 D)
D) 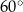
Miara kąta wpisanego w okrąg jest o 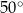 mniejsza od miary kąta środkowego opartego na tym samym łuku. Zatem miara kąta wpisanego jest równa
mniejsza od miary kąta środkowego opartego na tym samym łuku. Zatem miara kąta wpisanego jest równa
A) 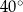 B)
B) 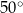 C)
C) 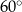 D)
D) 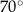
W okręgu 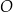 kąt środkowy
kąt środkowy 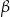 oraz kąt wpisany
oraz kąt wpisany  są oparte na tym samym łuku. Kąt
są oparte na tym samym łuku. Kąt 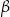 ma miarę o
ma miarę o 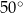 większą od kąta
większą od kąta  . Miara kąta
. Miara kąta 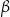 jest równa
jest równa
A) 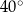 B)
B) 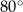 C)
C) 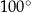 D)
D) 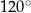
W okręgu 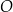 kąt środkowy
kąt środkowy 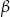 oraz kąt wpisany
oraz kąt wpisany  są oparte na tym samym łuku. Kąt
są oparte na tym samym łuku. Kąt 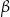 ma miarę o
ma miarę o 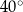 większą od kąta
większą od kąta  . Miara kąta
. Miara kąta 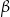 jest równa
jest równa
A) 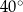 B)
B) 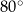 C)
C) 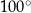 D)
D) 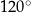
Kąt środkowy i kąt wpisany są oparte na tym samym łuku. Suma ich miar jest równa 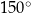 . Jaka jest miara kąta środkowego?
. Jaka jest miara kąta środkowego?
A) 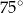 B)
B) 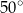 C)
C) 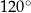 D)
D) 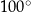
Kąt środkowy i kąt wpisany w okrąg są oparte na tym samym łuku. Suma ich miar jest równa 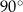 . Miara kata środkowego jest równa
. Miara kata środkowego jest równa
A) 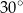 B)
B) 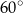 C)
C) 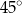 D)
D)