Na okręgu o środku w punkcie 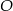 leżą punkty
leżą punkty 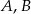 i
i 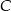 (zobacz rysunek). Kąt
(zobacz rysunek). Kąt 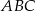 ma miarę
ma miarę 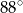 , a kąt
, a kąt 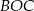 ma miarę o
ma miarę o 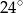 mniejszą od miary kąta
mniejszą od miary kąta 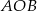 .
.
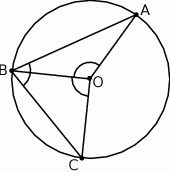
Kąt 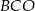 ma miarę
ma miarę
A) 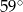 B)
B) 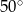 C)
C) 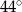 D)
D) 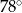
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Na okręgu o środku w punkcie 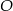 leżą punkty
leżą punkty 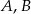 i
i 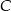 (zobacz rysunek). Kąt
(zobacz rysunek). Kąt 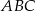 ma miarę
ma miarę 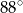 , a kąt
, a kąt 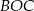 ma miarę o
ma miarę o 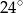 mniejszą od miary kąta
mniejszą od miary kąta 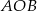 .
.

Kąt 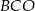 ma miarę
ma miarę
A) 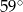 B)
B) 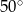 C)
C) 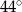 D)
D) 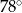
W trójkącie 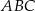 dane są wierzchołki
dane są wierzchołki 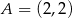 ,
, 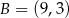 ,
, 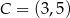 . Trójkąt
. Trójkąt 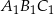 jest obrazem trójkąta
jest obrazem trójkąta 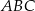 w jednokładności o środku
w jednokładności o środku 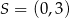 i skali
i skali 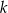 . Trójkąty te leżą po przeciwnych stronach osi rzędnych. Promień okręgu opisanego na trójkącie
. Trójkąty te leżą po przeciwnych stronach osi rzędnych. Promień okręgu opisanego na trójkącie 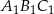 ma długość
ma długość 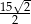 . Skala jednokładności
. Skala jednokładności 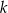 wynosi
wynosi
A) 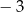 B)
B) 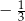 C)
C) 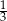 D) 3
D) 3
Liczba 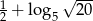 jest równa:
jest równa:
A) 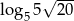 B)
B) 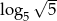 C)
C) 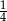 D)
D) 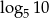
Spodnie po obniżce ceny o 30% kosztują 126 zł. Ile kosztowały spodnie przed obniżką?
A) 163,80 zł B) 180 zł C) 294 zł D) 420 zł
Cena roweru po obniżce o 15% była równa 850 zł. Przed obniżką ten rower kosztował
A) 865,00 zł B) 850,15 zł C) 1000,00 zł D) 977,50 zł
Cena książki wzrosła o 15% i wynosi 92 zł. Ile kosztowała książka przed podwyżką?
A) 105,8 zł B) 77 zł C) 78,2 zł D) 80 zł
Spodnie po obniżce ceny o 25% kosztują 168 zł. Ile kosztowały spodnie przed obniżką?
A) 193 zł B) 210 zł C) 224 zł D) 336 zł
Koszt uczestnictwa w obozie sportowym w 2018 r. wynosi 1620 zł. Wzrósł on w stosunku do kosztu z 2017 r. o 35%. Koszt uczestnictwa w obozie w 2017 r. wynosił
A) 1215 zł B) 1053 zł C) 1200 zł D) 567 zł
Medyczna maseczka ochronna wielokrotnego użytku z wymiennymi filtrami wskutek podwyżki zdrożała o 40% i kosztuje obecnie 106,40 zł. Cena maseczki przed podwyżką była równa
A) 63,84 zł B) 65,40 zł C) 76,00 zł D) 66,40 zł
Ostrosłup ma 12 krawędzi. Liczba wszystkich wierzchołków tego ostrosłupa jest równa
A) 12 B) 9 C) 8 D) 7
Jeśli ostrosłup ma 50 krawędzi, to liczba jego ścian jest równa
A) 50 B) 26 C) 25 D) 22
Ostrosłup, który ma 12 krawędzi, ma
A) 6 ścian B) 7 ścian C) 8 ścian D) 9 ścian
Jeżeli ostrosłup ma 10 krawędzi, to liczba ścian bocznych jest równa
A) 5 B) 7 C) 8 D) 10
Przekątne trapezu 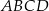 przecinają się w punkcie
przecinają się w punkcie 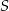 w ten sposób, że
w ten sposób, że 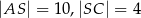 ,
, 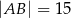 .
.
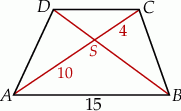
Długość odcinka 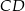 jest równa
jest równa
A) 4 B) 6 C) 8 D) 9
Miara kąta ostrego przecięcia prostych przedstawionych na rysunku wynosi
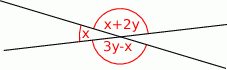
A) 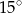 B)
B) 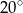 C)
C) 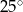 D)
D) 
Miara kąta ostrego przecięcia prostych przedstawionych na rysunku wynosi
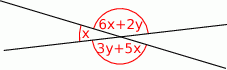
A)  B)
B)  C)
C) 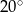 D)
D) 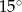
Miara kąta ostrego przecięcia prostych przedstawionych na rysunku wynosi
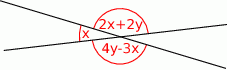
A) 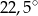 B)
B) 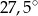 C)
C) 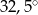 D)
D) 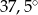
Wartość wyrażenia 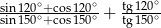 jest równa
jest równa
A) 4 B) 0 C) 1 D) 2
Przyprostokątna 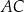 trójkąta prostokątnego
trójkąta prostokątnego 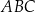 ma długość 8 oraz
ma długość 8 oraz 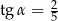 (zobacz rysunek).
(zobacz rysunek).
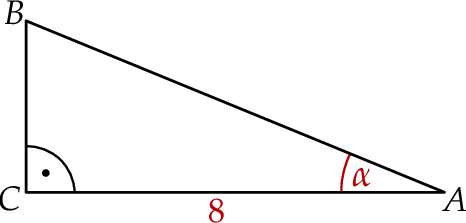
Pole tego trójkąta jest równe
A) 12 B) 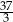 C)
C) 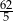 D)
D) 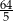
Przyprostokątna 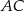 trójkąta prostokątnego
trójkąta prostokątnego 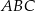 ma długość 14 oraz
ma długość 14 oraz 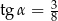 (zobacz rysunek).
(zobacz rysunek).
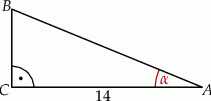
Pole tego trójkąta jest równe
A) 73,5 B) 36,75 C) 5,25 D) 37,3
Ile jest liczb naturalnych trzycyfrowych, których iloczyn cyfr jest równy 0?
A) 162 B) 90 C) 171 D) 172
Ile jest liczb naturalnych czterocyfrowych o różnych cyfrach, których iloczyn cyfr jest równy 0?
A) 1728 B) 504 C) 720 D) 1512
Prosta o równaniu 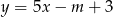 przechodzi przez punkt
przechodzi przez punkt 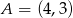 . Wtedy
. Wtedy
A) 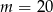 B)
B) 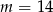 C)
C) 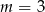 D)
D) 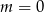
Prosta o równaniu 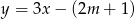 przecina w układzie współrzędnych oś
przecina w układzie współrzędnych oś 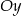 w punkcie
w punkcie 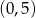 . Wtedy
. Wtedy
A) 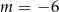 B)
B) 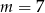 C)
C) 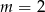 D)
D) 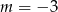
Na płaszczyźnie, w kartezjańskim układzie współrzędnych 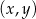 , dana jest prosta
, dana jest prosta 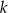 o równaniu
o równaniu 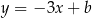 , przechodząca przez punkt
, przechodząca przez punkt 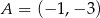 . Współczynnik
. Współczynnik 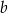 w równaniu tej prostej jest równy
w równaniu tej prostej jest równy
A) 0 B) 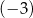 C)
C) 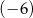 D)
D) 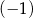
Prosta o równaniu 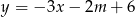 przechodzi przez punkt
przechodzi przez punkt 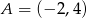 . Wtedy
. Wtedy
A) 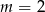 B)
B) 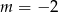 C)
C) 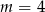 D)
D) 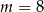
Prosta o równaniu 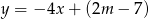 przechodzi przez punkt
przechodzi przez punkt 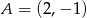 . Wtedy
. Wtedy
A) 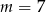 B)
B) 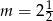 C)
C) 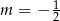 D)
D) 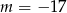
Prosta o równaniu 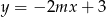 przechodzi przez punkt
przechodzi przez punkt 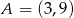 . Wtedy
. Wtedy
A) 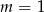 B)
B) 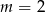 C)
C) 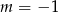 D)
D) 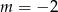
Prosta o równaniu 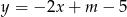 przechodzi przez punkt
przechodzi przez punkt 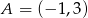 . Wtedy
. Wtedy
A) 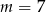 B)
B) 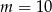 C)
C) 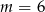 D)
D) 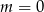
Punkt o współrzędnych 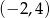 należy do prostej
należy do prostej 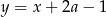 . Zatem
. Zatem
A) 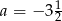 B)
B) 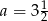 C)
C) 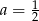 D)
D) 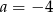
Na płaszczyźnie, w kartezjańskim układzie współrzędnych 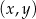 , dana jest prosta
, dana jest prosta 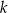 o równaniu
o równaniu 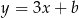 , przechodząca przez punkt
, przechodząca przez punkt 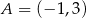 . Współczynnik
. Współczynnik 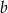 w równaniu tej prostej jest równy
w równaniu tej prostej jest równy
A) 0 B) 6 C) 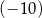 D) 8
D) 8
Prosta o równaniu 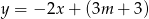 przecina w układzie współrzędnych oś
przecina w układzie współrzędnych oś 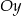 w punkcie
w punkcie 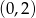 . Wtedy
. Wtedy
A) 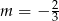 B)
B) 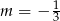 C)
C) 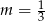 D)
D) 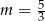
Osią symetrii paraboli będącej wykresem funkcji 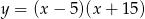 jest prosta o równaniu
jest prosta o równaniu
A) 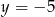 B)
B) 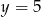 C)
C) 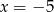 D)
D) 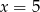
Wykresem funkcji kwadratowej 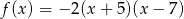 jest parabola której oś symetrii ma równanie
jest parabola której oś symetrii ma równanie
A) 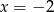 B)
B) 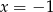 C)
C) 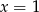 D)
D) 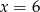
Wykresem funkcji kwadratowej 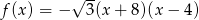 jest parabola której oś symetrii ma równanie
jest parabola której oś symetrii ma równanie
A) 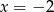 B)
B) 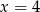 C)
C) 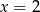 D)
D) 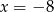
Osią symetrii paraboli będącej wykresem funkcji 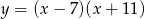 jest prosta o równaniu
jest prosta o równaniu
A) 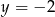 B)
B) 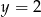 C)
C) 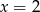 D)
D) 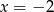
Oś symetrii paraboli, która jest wykresem funkcji 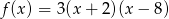 ma równanie
ma równanie
A) 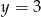 B)
B) 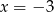 C)
C) 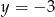 D)
D) 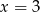
Osią symetrii paraboli określonej wzorem 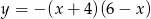 jest prosta o równaniu
jest prosta o równaniu
A) 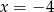 B)
B) 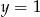 C)
C) 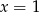 D)
D) 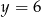
Średnia arytmetyczna trzech liczb: 12, 14, 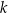 , jest równa 16. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
, jest równa 16. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Liczba 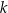 jest równa 22. jest równa 22. | P | F |
Średnia arytmetyczna liczb: 12, 14, 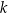 , 11, 17, jest większa od 16. , 11, 17, jest większa od 16. | P | F |
Dany jest sześcian 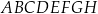 o krawędzi długości 5. Wewnątrz sześcianu znajduje się punkt
o krawędzi długości 5. Wewnątrz sześcianu znajduje się punkt 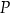 (zobacz rysunek).
(zobacz rysunek).
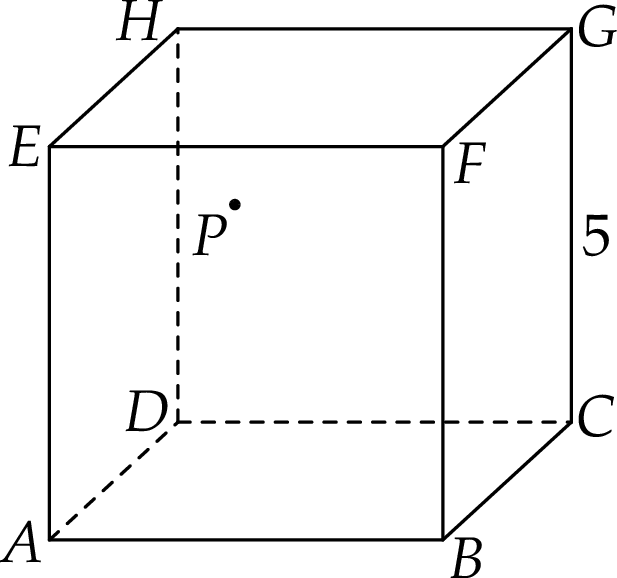
Suma odległości punktu 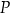 od wszystkich ścian sześcianu
od wszystkich ścian sześcianu 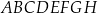 jest równa
jest równa
A) 15 B) 20 C) 25 D) 30
Doświadczenie losowe polega na rzucie dwiema symetrycznymi monetami i sześcienną kostką do gry. Prawdopodobieństwo zdarzenia polegającego na tym, że wynikiem rzutu są dwa orły i sześć oczek na kostce, jest równe
A) 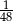 B)
B) 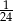 C)
C) 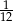 D)
D) 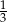
Doświadczenie losowe polega na rzucie dwiema symetrycznymi monetami i sześcienną kostką do gry. Prawdopodobieństwo zdarzenia polegającego na tym, że wynikiem rzutu jest co najmniej jedna reszka i trzy oczka na kostce, jest równe
A) 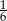 B)
B) 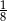 C)
C) 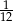 D)
D) 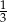
Jeśli w ciągu arytmetycznym 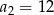 i
i 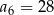 , to
, to
A) 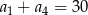 B)
B) 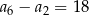 C)
C) 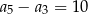 D)
D) 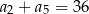
Trzywyrazowy ciąg 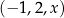 jest arytmetyczny. Trzywyrazowy ciąg
jest arytmetyczny. Trzywyrazowy ciąg 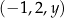 jest geometryczny. Liczby
jest geometryczny. Liczby  oraz
oraz 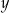 spełniają warunki
spełniają warunki
A) 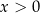 i
i 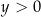 B)
B) 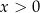 i
i 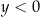 C)
C) 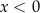 i
i 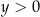 D)
D) 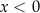 i
i 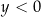
Rozwiązaniem równania 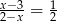 jest liczba
jest liczba
A) 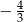 B)
B) 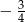 C)
C) 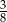 D)
D) 
Rozwiązaniem równania 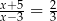 jest liczba
jest liczba
A) 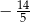 B)
B) 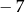 C)
C) 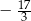 D)
D) 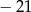
Dla jakiego argumentu funkcja 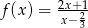 przyjmuje wartość 3?
przyjmuje wartość 3?
A) 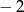 B) 2 C) 3 D) 0
B) 2 C) 3 D) 0
Dla jakiego argumentu funkcja 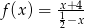 przyjmuje wartość 2?
przyjmuje wartość 2?
A) 1 B) 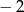 C)
C) 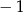 D) 2
D) 2
Rozwiązaniem równania 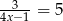 jest liczba
jest liczba
A) 1 B) 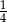 C)
C) 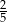 D)
D) 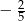
Rozwiązaniem równania 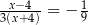 jest liczba
jest liczba
A) 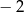 B) 2 C) 4 D)
B) 2 C) 4 D) 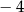
Rozwiązaniem równania 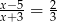 jest liczba
jest liczba
A) 21 B) 7 C) 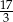 D) 0
D) 0
Rozwiązaniem równania 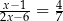 jest liczba
jest liczba
A) 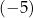 B)
B) 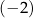 C) 1 D) 17
C) 1 D) 17
Rozwiązaniem równania 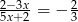 jest
jest
A) 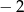 B)
B) 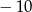 C)
C) 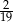 D)
D) 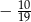
Rozwiązaniem równania 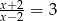 (
(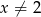 ) jest liczba
) jest liczba
A) 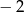 B) 3 C) 4 D)
B) 3 C) 4 D) 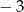
Rozwiązaniem równania 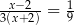 jest liczba
jest liczba
A) 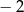 B) 2 C) 4 D)
B) 2 C) 4 D) 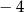
Rozwiązaniem równania 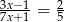 jest
jest
A) 1 B) 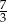 C)
C)  D) 7
D) 7
Rozwiązaniem równania 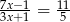 jest
jest
A) 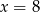 B)
B) 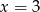 C)
C) 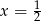 D)
D) 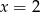
Rozwiązaniem równania 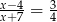 jest liczba
jest liczba
A) 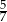 B) 5 C) 37 D)
B) 5 C) 37 D) 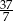
Rozwiązaniem równania 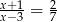 jest liczba
jest liczba
A) 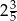 B)
B) 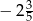 C)
C) 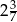 D)
D) 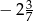
Rozwiązaniem równania 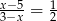 jest liczba
jest liczba
A) 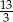 B)
B) 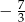 C)
C) 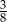 D)
D) 
Dla jakiego argumentu funkcja 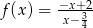 przyjmuje wartość 4?
przyjmuje wartość 4?
A) 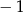 B) 0 C) 1 D) 2
B) 0 C) 1 D) 2
Rozwiązaniem równania 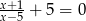 jest liczba
jest liczba
A) 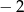 B) 2 C) 4 D)
B) 2 C) 4 D) 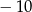
Rozwiązaniem równania 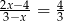 jest liczba
jest liczba
A) 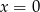 B)
B) 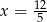 C)
C) 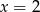 D)
D) 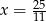
Rozwiązaniem równania 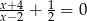 jest liczba
jest liczba
A) 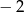 B) 2 C)
B) 2 C) 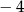 D)
D) 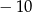
Rozwiązaniem równania 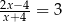 (
(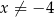 ) jest liczba
) jest liczba
A) 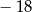 B)
B) 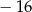 C) 16 D) 18
C) 16 D) 18
Rozwiązaniem równania 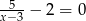 jest liczba
jest liczba
A) 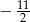 B)
B) 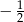 C)
C) 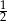 D)
D) 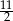
Rozwiązaniem równania 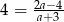 jest liczba
jest liczba
A) 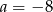 B)
B) 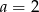 C)
C) 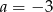 D)
D) 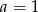
Rozwiązaniem równania 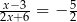 jest liczba
jest liczba
A) 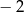 B) 2 C) 4 D)
B) 2 C) 4 D) 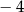
Rozwiązaniem równania 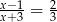 jest liczba
jest liczba
A) 1 B) 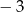 C) 9 D)
C) 9 D) 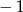
Miejscem zerowym funkcji 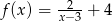 jest
jest
A) 3 B) 2 C) 2,5 D) -3
Rozwiązaniem równania 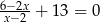 jest liczba
jest liczba
A) 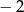 B) 2 C)
B) 2 C) 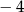 D) równanie nie ma rozwiązania
D) równanie nie ma rozwiązania
Rozwiązaniem równania 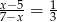 jest liczba
jest liczba
A) 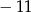 B)
B) 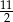 C)
C) 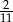 D) 11
D) 11
Rozwiązaniem równania 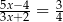 jest
jest
A) 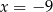 B)
B) 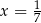 C)
C) 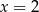 D)
D) 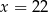
Zbiorem wartości funkcji 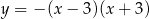 określonej dla
określonej dla 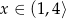 jest przedział
jest przedział
A) 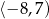 B)
B) 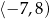 C)
C) 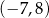 D)
D) 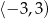
Zbiorem wartości funkcji 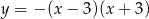 określonej dla
określonej dla 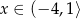 jest przedział
jest przedział
A) 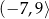 B)
B) 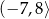 C)
C) 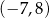 D)
D) 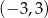
Pole figury ograniczonej fragmentem wykresu funkcji 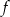 danej wzorem
danej wzorem 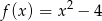 i osią
i osią 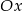 jest
jest
A) mniejsze od 8 B) większe od 8 C) równe 8 D) większe od 16
Pole figury ograniczonej fragmentem wykresu funkcji 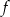 danej wzorem
danej wzorem 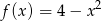 i osią
i osią 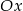 jest
jest
A) mniejsze od 16 B) mniejsze od 8 C) równe 16 D) większe od 16
Pole figury ograniczonej fragmentem wykresu funkcji 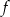 danej wzorem
danej wzorem 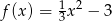 i osią
i osią 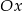 jest
jest
A) mniejsze od 9 B) równe 18 C) większe od 9 D) większe od 18
