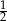Funkcja 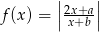 jest funkcją malejącą w przedziale
jest funkcją malejącą w przedziale 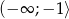 oraz
oraz 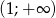 , rosnącą w przedziale
, rosnącą w przedziale 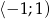 , a do jej wykresu należy punkt
, a do jej wykresu należy punkt 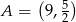 . Zatem wzór funkcji
. Zatem wzór funkcji 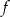 ma postać
ma postać
A) 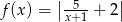 B)
B) 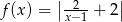 C)
C) 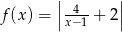 D)
D) 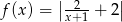
/Szkoła średnia/Zadania testowe
Średnia arytmetyczna wszystkich liczb pierwszych należących do przedziału 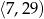 jest równa
jest równa
A) 15 B) 16,6 C) 17 D) 18,6
Średnia arytmetyczna wszystkich liczb pierwszych należących do przedziału 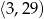 jest równa
jest równa
A) 14,1 B) 11,5 C) 12,25 D) 12,4
Dany jest przedział liczbowy 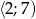 . Średnia arytmetyczna liczb pierwszych należących do tego przedziału jest równa
. Średnia arytmetyczna liczb pierwszych należących do tego przedziału jest równa
A) 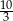 B)
B) 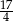 C) 4 D) 5
C) 4 D) 5
Średnia arytmetyczna wszystkich liczb pierwszych należących do przedziału 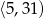 jest równa
jest równa
A) 17,2 B) 15,5 C) 16,3 D) 15,9
W pewnym banku oprocentowanie kredytu konsumpcyjnego przez cały marzec było równe 17%. Na początku kwietnia podwyższono oprocentowanie tego kredytu o 3 punkty procentowe, a na początku maja obniżono o 4 punkty procentowe. Oznacza to, że oprocentowanie tego kredytu konsumpcyjnego między kwietniem a majem zmalało o
A) 5% B) 3% C) 25% D) 20%
Jeśli przyprostokątne trójkąta prostokątnego są równe 6 i 3, a najmniejszy kąt ma miarę  , to wyrażenie
, to wyrażenie 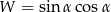 ma wartość
ma wartość
A) 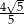 B)
B) 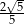 C)
C)  D)
D) 
W trójkącie prostokątnym o przyprostokątnych długości 1 i 2 kąty ostre są równe  i
i 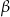 (
(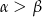 ). Wartość wyrażenia
). Wartość wyrażenia 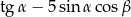 jest równe
jest równe
A) 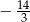 B) -2 C) 0 D)
B) -2 C) 0 D) 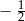
Pole powierzchni jednej ze ścian ołowianej kostki do gry jest równe 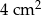 . Gęstość ołowiu jest równa ok.
. Gęstość ołowiu jest równa ok. 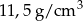 . Masa kostki jest równa około
. Masa kostki jest równa około
A) 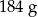 B)
B) 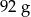 C)
C) 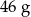 D)
D) 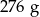
Pole powierzchni jednej ze ścian stalowej kostki do gry jest równe 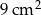 . Gęstość stali jest równa ok.
. Gęstość stali jest równa ok. 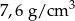 . Masa kostki jest równa około
. Masa kostki jest równa około
A) 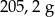 B)
B) 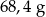 C)
C) 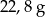 D)
D) 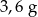
Pole powierzchni jednej ze ścian aluminiowej kostki do gry jest równe 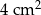 . Gęstość aluminium jest równa ok.
. Gęstość aluminium jest równa ok. 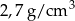 . Masa kostki jest równa około
. Masa kostki jest równa około
A) 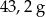 B)
B) 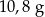 C)
C) 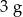 D)
D) 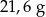
Ze zbioru 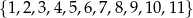 losujemy bez zwracania dwa razy po jednej liczbie. Wylosowane liczby tworzą parę
losujemy bez zwracania dwa razy po jednej liczbie. Wylosowane liczby tworzą parę 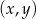 , gdzie
, gdzie  jest pierwszą wylosowaną liczbą,
jest pierwszą wylosowaną liczbą, 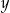 jest drugą wylosowaną liczbą. Wszystkich par
jest drugą wylosowaną liczbą. Wszystkich par 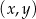 takich, że suma
takich, że suma 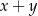 jest liczbą parzystą jest
jest liczbą parzystą jest
A) 20 B) 25 C) 50 D) 61
Jaki jest wzór funkcji kwadratowej, której wykres przedstawiono na rysunku?
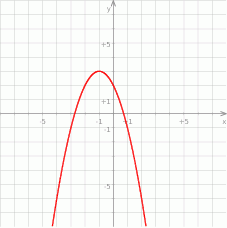
A) 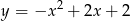 B)
B) 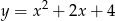 C)
C) 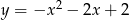 D)
D) 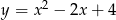
Jaki jest wzór funkcji kwadratowej, której wykres przedstawiono na rysunku?
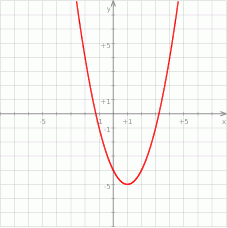
A) 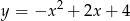 B)
B) 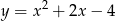 C)
C) 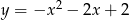 D)
D) 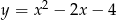
Na rysunku przedstawiono fragment wykresu funkcji kwadratowej 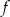 .
.
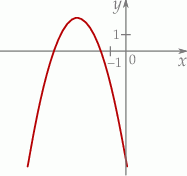
Jeden spośród podanych poniżej wzorów jest wzorem tej funkcji. Wskaż wzór funkcji 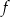 .
.
A) 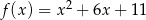 B)
B) 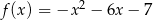
C) 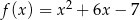 D)
D) 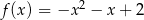
Na rysunku przedstawiono fragment wykresu funkcji kwadratowej 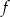 .
.
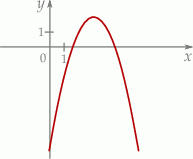
Jeden spośród podanych poniżej wzorów jest wzorem tej funkcji. Wskaż wzór funkcji 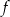 .
.
A) 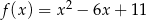 B)
B) 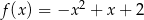
C) 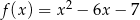 D)
D) 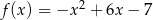
Dany jest fragment wykresu pewnej funkcji kwadratowej 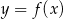 . Funkcja ta ma wzór
. Funkcja ta ma wzór
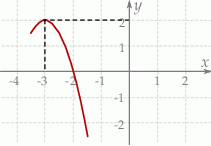
A) 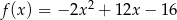 B)
B) 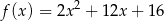
C) 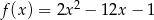 D)
D) 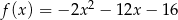
Wzorem funkcji kwadratowej 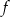 , której fragment wykresu przedstawiono na rysunku jest:
, której fragment wykresu przedstawiono na rysunku jest:
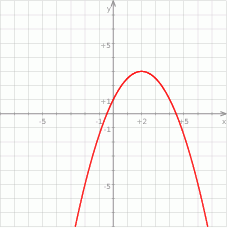
A) 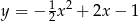 B)
B) 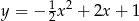 C)
C) 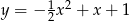 D)
D) 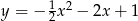
Średnia arytmetyczna wszystkich liczb złożonych należących do przedziału 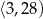 z dokładnością do 0,1 jest równa
z dokładnością do 0,1 jest równa
A) 16,9 B) 17,4 C) 16,3 D) 16,7
Ile jest wszystkich czterocyfrowych liczb naturalnych podzielnych przez 3?
A) 3000 B) 3333 C) 2999 D) 2998
Ile jest wszystkich czterocyfrowych liczb naturalnych podzielnych przez 7?
A) 1285 B) 1428 C) 1284 D) 1286
Ile jest wszystkich liczb naturalnych czterocyfrowych mniejszych od 2021 i podzielnych przez 3?
A) 673 B) 334 C) 340 D) 339
Ile jest wszystkich liczb naturalnych czterocyfrowych mniejszych od 2018 i podzielnych przez 5?
A) 402 B) 403 C) 203 D) 204
Ile jest wszystkich liczb naturalnych czterocyfrowych podzielnych przez 5?
A) 2000 B) 1800 C) 1000 D) 900
Ile jest wszystkich liczb naturalnych trzycyfrowych podzielnych przez 5?
A) 90 B) 100 C) 180 D) 200
Ile jest wszystkich pięciocyfrowych liczb naturalnych podzielnych przez 29?
A) 3103 B) 3105 C) 3104 D) 3106
Ile jest wszystkich liczb naturalnych czterocyfrowych mniejszych od 2020 i podzielnych przez 4?
A) 506 B) 505 C) 256 D) 255
Ile jest wszystkich czterocyfrowych liczb naturalnych podzielnych przez 13?
A) 692 B) 691 C) 690 D) 693
Ile jest wszystkich liczb naturalnych czterocyfrowych mniejszych od 2019 i podzielnych przez 4?
A) 256 B) 257 C) 255 D) 128
Punkty 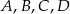 dzielą okrąg o środku
dzielą okrąg o środku 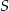 w stosunku
w stosunku 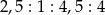 .
.
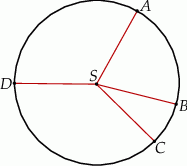
Różnica miar kątów wypukłych 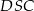 i
i 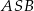 jest równa
jest równa
A) 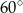 B)
B) 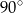 C)
C) 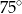 D)
D) 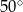
Ciąg 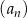 jest określony wzorem
jest określony wzorem 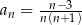 dla każdej liczby naturalnej
dla każdej liczby naturalnej 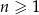 . Wynika stąd, że suma siedmiu początkowych wyrazów ciągu
. Wynika stąd, że suma siedmiu początkowych wyrazów ciągu 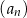 jest większa od sumy pięciu początkowych wyrazów ciągu
jest większa od sumy pięciu początkowych wyrazów ciągu 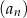 o
o
A)  B)
B) 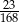 C)
C) 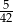 D) 0
D) 0
W pudełku znajdują się dwie kule: niebieska i czerwona. Dziewięciokrotnie losujemy ze zwracaniem jedną kulę z tego pudełka. Prawdopodobieństwo zdarzenia polegającego na tym, że dokładnie osiem z wylosowanych kul jest tego samego koloru jest równe
A) 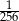 B)
B) 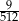 C)
C) 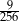 D)
D) 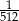
W pudełku znajdują się dwie kule: niebieska i czerwona. Ośmiokrotnie losujemy ze zwracaniem jedną kulę z tego pudełka. Prawdopodobieństwo zdarzenia polegającego na tym, że dokładnie siedem z wylosowanych kul jest tego samego koloru jest równe
A) 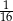 B)
B) 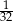 C)
C) 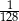 D)
D) 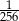
Dany jest trójkąt o bokach długości 4, 5 oraz 6. Cosinus największego kąta wewnętrznego tego trójkąta jest równy
A) 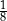 B)
B) 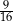 C)
C)  D)
D) 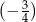
Po rozłożeniu na czynniki wyrażenie 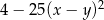 ma postać
ma postać
A) 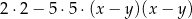 B)
B) 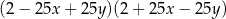
C) 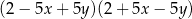 D)
D) 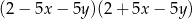
Po rozłożeniu na czynniki wyrażenie 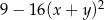 ma postać
ma postać
A) 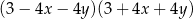 B)
B) 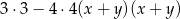
C) 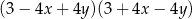 D)
D) 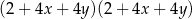
Po rozłożeniu na czynniki wyrażenie 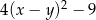 ma postać
ma postać
A) 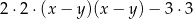 B)
B) 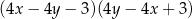
C) 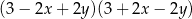 D)
D) 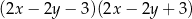
Jeżeli kąt ostry  jest o
jest o 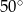 mniejszy od kąta przyległego do niego, to
mniejszy od kąta przyległego do niego, to
A) 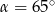 B)
B) 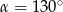 C)
C) 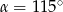 D)
D) 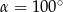
Jeżeli kąt ostry  jest o
jest o 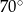 mniejszy od kąta przyległego do niego, to
mniejszy od kąta przyległego do niego, to
A) 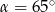 B)
B) 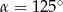 C)
C) 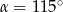 D)
D) 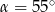
Jeżeli kąt ostry  jest o
jest o 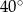 mniejszy od kąta przyległego do niego, to
mniejszy od kąta przyległego do niego, to
A) 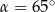 B)
B) 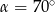 C)
C) 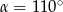 D)
D) 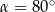
Oblicz długość odcinka 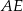 wiedząc, że
wiedząc, że 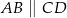 i
i 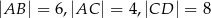 .
.
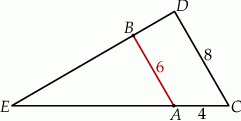
A) 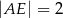 B)
B) 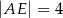 C)
C) 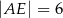 D)
D) 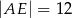
W trójkącie 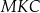 bok
bok 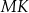 ma długość 24. Prosta równoległa do boku
ma długość 24. Prosta równoległa do boku 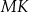 przecina boki
przecina boki 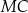 i
i 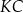 – odpowiednio – w punktach
– odpowiednio – w punktach 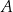 oraz
oraz 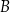 takich, że
takich, że 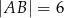 i
i 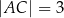 (zobacz rysunek).
(zobacz rysunek).

Długość odcinka 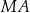 jest równa
jest równa
A) 18 B) 15 C) 9 D) 12
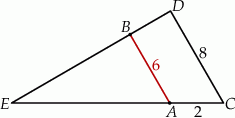
Oblicz długość odcinka 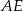 wiedząc, że
wiedząc, że 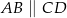 i
i 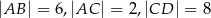 .
.
A) 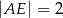 B)
B) 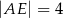 C)
C) 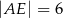 D)
D) 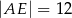
W trójkącie 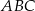 punkt
punkt 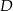 leży na boku
leży na boku 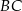 , a punkt
, a punkt 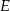 leży na boku
leży na boku 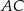 . Odcinek
. Odcinek 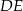 jest równoległy do boku
jest równoległy do boku 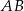 , a ponadto
, a ponadto 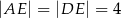 ,
, 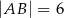 (zobacz rysunek).
(zobacz rysunek).
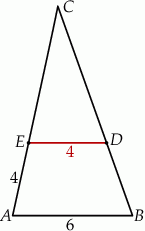
Odcinek 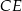 ma długość
ma długość
A) 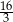 B)
B)  C) 8 D) 6
C) 8 D) 6
W trójkącie 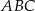 punkt
punkt 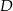 leży na boku
leży na boku 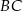 , a punkt
, a punkt 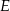 leży na boku
leży na boku 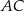 . Odcinek
. Odcinek 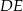 jest równoległy do boku
jest równoległy do boku 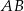 , a ponadto
, a ponadto 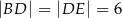 ,
, 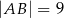 (zobacz rysunek).
(zobacz rysunek).
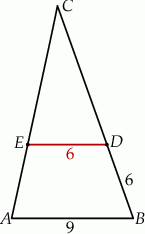
Odcinek 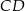 ma długość
ma długość
A) 8 B) 4 C) 9 D) 12
Oblicz długość odcinka 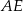 wiedząc, że
wiedząc, że 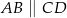 i
i 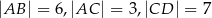 .
.
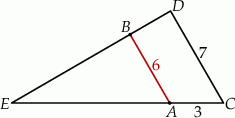
A) 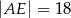 B)
B) 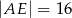 C)
C) 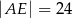 D)
D) 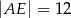
Jeżeli odcinki 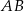 i
i 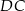 są równoległe, to długość odcinka
są równoległe, to długość odcinka 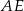 (patrz rys.) jest równa
(patrz rys.) jest równa
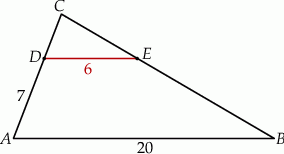
A) 9 B) 10 C) 11 D) 12
Odcinki 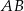 i
i 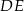 są równoległe. Długości odcinków
są równoległe. Długości odcinków 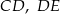 i
i 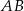 są odpowiednio równe 2, 5 i 15.
są odpowiednio równe 2, 5 i 15.
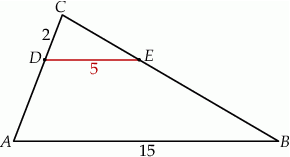
Długość odcinka 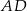 jest równa
jest równa
A) 3 B) 4 C) 5 D) 6
Odcinki 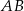 i
i 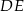 są równoległe. Długości odcinków
są równoległe. Długości odcinków 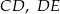 i
i 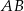 są odpowiednio równe 2, 4 i 16.
są odpowiednio równe 2, 4 i 16.
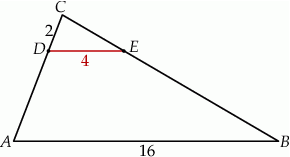
Długość odcinka 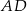 jest równa
jest równa
A) 12 B) 8 C) 3 D) 6
Odcinki 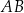 i
i 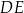 są równoległe. Długości odcinków
są równoległe. Długości odcinków 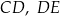 i
i 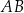 są odpowiednio równe 1, 3 i 9.
są odpowiednio równe 1, 3 i 9.
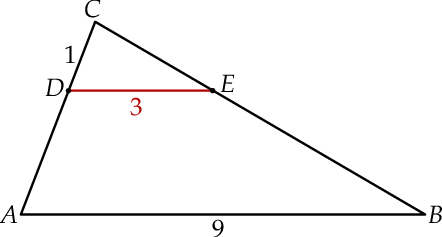
Długość odcinka 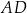 jest równa
jest równa
A) 2 B) 3 C) 5 D) 6
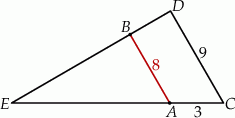
Oblicz długość odcinka 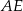 wiedząc, że
wiedząc, że 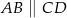 i
i 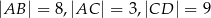 .
.
A) 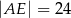 B)
B) 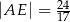 C)
C) 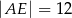 D)
D) 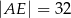
Liczba  jest ujemna, a liczba
jest ujemna, a liczba 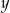 jest dodatnia. Wartość ujemną przyjmuje wyrażenie
jest dodatnia. Wartość ujemną przyjmuje wyrażenie
A) 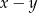 B)
B) 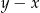 C)
C) 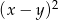 D)
D) 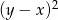
Liczba  jest ujemna, a liczba
jest ujemna, a liczba 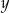 jest dodatnia. Wartość dodatnią przyjmuje wyrażenie
jest dodatnia. Wartość dodatnią przyjmuje wyrażenie
A) 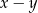 B)
B) 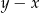 C)
C) 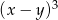 D)
D) 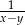
Liczba  jest dodatnia, a liczba
jest dodatnia, a liczba 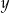 jest ujemna. Wartość ujemną przyjmuje wyrażenie
jest ujemna. Wartość ujemną przyjmuje wyrażenie
A) 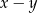 B)
B) 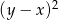 C)
C) 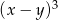 D)
D) 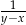
Liczba  jest ujemna, a liczba
jest ujemna, a liczba 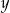 jest dodatnia. Wartość ujemną przyjmuje wyrażenie
jest dodatnia. Wartość ujemną przyjmuje wyrażenie
A) 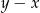 B)
B) 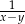 C)
C) 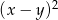 D)
D) 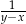
Każda krawędź graniastosłupa prawidłowego sześciokątnego ma długość równą 2 (zobacz rysunek).
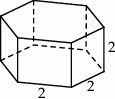
Pole powierzchni całkowitej tego graniastosłupa jest równe
A) 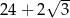 B)
B) 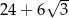 C)
C) 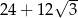 D)
D) 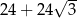
Każda krawędź graniastosłupa prawidłowego sześciokątnego ma długość równą 6. Pole powierzchni całkowitej tego graniastosłupa jest równe
A) 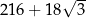 B)
B) 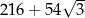 C)
C) 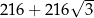 D)
D) 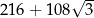
Każda krawędź graniastosłupa prawidłowego sześciokątnego ma długość równą 3 (zobacz rysunek).
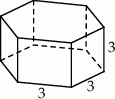
Pole powierzchni całkowitej tego graniastosłupa jest równe
A) 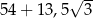 B)
B) 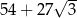 C)
C) 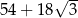 D)
D) 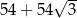
Suma długości wszystkich krawędzi sześcianu jest równa 24. Objętość tego sześcianu jest równa
A) 8 B) 27 C) 24 D) 64
Suma wszystkich krawędzi sześcianu jest równa 36. Objętość tego sześcianu jest równa
A) 8 B) 27 C) 64 D) 24
Suma długości wszystkich krawędzi sześcianu jest równa 72. Objętość tego sześcianu jest równa
A) 1728 B) 216 C) 127 D) 81
Cosinus kąta dwuściennego utworzonego przez dwie sąsiednie ściany czworościanu foremnego jest równy
A) 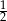 B)
B) 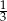 C)
C)  D)
D) 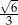
W czworościanie foremnym cosinus kąta dwuściennego między dwiema sąsiednimi ścianami jest równy
A) 0 B) 0,25 C) 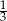 D)
D)