Jeśli dla kąta ostrego 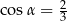 , to
, to
A) 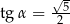 B)
B) 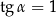 C)
C) 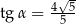 D)
D) 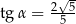
/Szkoła średnia/Zadania testowe
Jeśli dla kąta ostrego 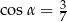 , to
, to
A) 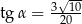 B)
B) 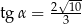 C)
C) 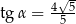 D)
D) 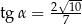
Kąt  jest ostry oraz
jest ostry oraz 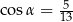 . Wtedy
. Wtedy
A) 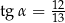 B)
B) 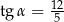 C)
C) 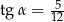 D)
D) 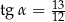
Jeśli dla kąta ostrego 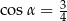 , to
, to
A) 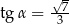 B)
B) 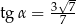 C)
C) 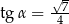 D)
D) 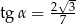
Cosinus kąta ostrego jest równy 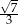 . Tangens tego kąta jest równy
. Tangens tego kąta jest równy
A) 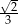 B)
B) 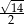 C)
C) 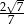 D)
D) 
Kąt  jest ostry oraz
jest ostry oraz 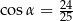 . Tangens kąta
. Tangens kąta  jest równy
jest równy
A) 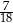 B)
B) 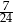 C)
C) 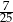 D)
D) 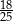
Kąt  jest ostry i
jest ostry i 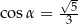 . Wobec tego
. Wobec tego
A) 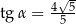 B)
B) 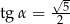 C)
C) 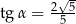 D)
D) 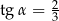
Kąt  jest ostry i
jest ostry i 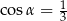 . Wobec tego
. Wobec tego
A) 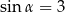 i
i 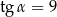 B)
B) 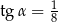 C)
C) 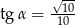 D)
D) 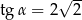
Cosinus kąta ostrego  jest równy
jest równy  . Wtedy
. Wtedy 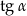 jest równy
jest równy
A) 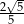 B)
B) 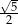 C) 2 D)
C) 2 D) 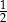
Przekrojem osiowym stożka o objętości 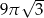 jest trójkąt równoboczny. Obwód tego trójkąta jest równy
jest trójkąt równoboczny. Obwód tego trójkąta jest równy
A) 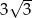 B)
B) 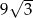 C) 18 D) 6
C) 18 D) 6
Wierzchołek paraboli o równaniu 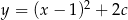 leży na prostej o równaniu
leży na prostej o równaniu 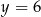 . Wtedy
. Wtedy
A) 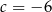 B)
B) 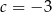 C)
C) 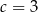 D)
D) 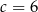
Wierzchołek paraboli o równaniu 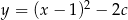 leży na prostej o równaniu
leży na prostej o równaniu 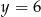 . Wtedy
. Wtedy
A) 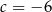 B)
B) 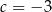 C)
C) 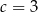 D)
D) 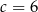
Jeśli wiadomo, że wierzchołek funkcji 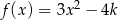 należy do prostej
należy do prostej 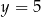 , to wartość liczbowa współczynnika
, to wartość liczbowa współczynnika 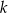 jest równa
jest równa
A) 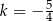 B)
B) 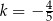 C)
C) 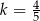 D)
D) 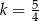
Wierzchołek paraboli o równaniu 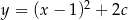 leży na prostej o równaniu
leży na prostej o równaniu 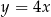 . Wtedy
. Wtedy
A) 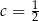 B)
B) 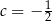 C)
C) 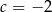 D)
D) 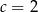
Wierzchołek paraboli o równaniu 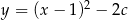 leży na prostej o równaniu
leży na prostej o równaniu 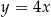 . Wtedy
. Wtedy
A) 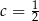 B)
B) 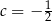 C)
C) 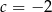 D)
D) 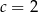
Przekrojem prostopadłościanu zawierającym przekątną podstawy i przekątne sąsiednich ścian bocznych wychodzących z tego samego wierzchołka jest
A) kwadrat B) prostokąt C) trójkąt D) trapez
Wykresem funkcji kwadratowej 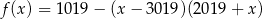 jest parabola, której wierzchołek leży na prostej
jest parabola, której wierzchołek leży na prostej
A) 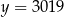 B)
B) 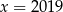 C)
C) 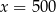 D)
D) 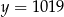
Prostokąt 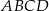 o przekątnej długości
o przekątnej długości 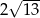 jest podobny do prostokąta o bokach długości 2 i 3. Obwód prostokąta
jest podobny do prostokąta o bokach długości 2 i 3. Obwód prostokąta 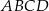 jest równy
jest równy
A) 10 B) 20 C) 5 D) 24
Prostokąt 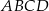 o przekątnej długości
o przekątnej długości 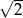 jest podobny do prostokąta o bokach długości 1 i 7. Obwód prostokąta
jest podobny do prostokąta o bokach długości 1 i 7. Obwód prostokąta 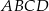 jest równy
jest równy
A) 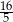 B)
B) 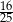 C) 80 D) 16
C) 80 D) 16
Prostokąt o bokach 4 i 6 obracając się dookoła prostej zawierającej dłuższy bok wyznacza bryłę o objętości równej
A) 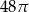 B)
B) 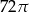 C)
C) 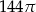 D)
D) 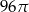
Prostokąt o bokach 10 i 6 obracając się dookoła prostej zawierającej dłuższy bok wyznacza bryłę o objętości równej
A) 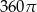 B)
B) 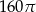 C)
C) 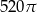 D)
D) 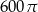
Prostokąt o bokach 3 i 5 obracając się dookoła prostej zawierającej dłuższy bok wyznacza bryłę o objętości równej
A) 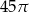 B)
B) 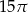 C)
C) 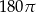 D)
D) 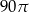
W pewnym sklepie ceny wszystkich płyt CD obniżono o 20%. Zatem za dwie płyty kupione w tym sklepie należy zapłacić mniej o
A) 10% B) 20% C) 30% D) 40%
Jeżeli 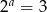 ,
, 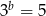 i
i 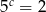 , to iloczyn
, to iloczyn 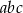 jest równy
jest równy
A) 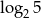 B)
B) 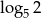 C) 1 D) 2
C) 1 D) 2
Jeżeli 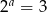 ,
, 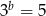 i
i 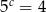 , to iloczyn
, to iloczyn 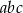 jest równy
jest równy
A) 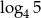 B)
B) 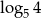 C) 4 D) 2
C) 4 D) 2
Sześcian wyrażenia 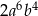 jest równy
jest równy
A) 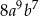 B)
B) 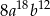 C)
C) 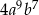 D)
D) 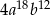
Sześcian wyrażenia 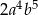 jest równy
jest równy
A) 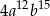 B)
B) 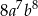 C)
C) 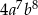 D)
D) 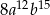
Kwadrat wyrażenia 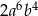 jest równy
jest równy
A) 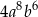 B)
B) 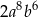 C)
C) 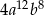 D)
D) 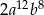
Która z liczb nie może być równa polu rombu o obwodzie 12?
A) 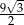 B)
B) 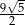 C)
C) 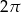 D)
D) 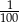
Która z liczb nie może być równa polu rombu o obwodzie 8?
A) 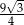 B)
B) 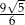 C)
C) 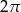 D)
D) 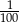
Liczba 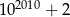 jest podzielna przez
jest podzielna przez
A) 10 B) 5 C) 6 D) 4
Liczba 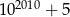 jest podzielna przez
jest podzielna przez
A) 10 B) 15 C) 6 D) 9
Liczba 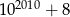 jest podzielna przez
jest podzielna przez
A) 18 B) 10 C) 15 D) 20
Ile procent doby stanowi 15 minut?
A) około 1% B) 4% C) około 2% D) 12,5%
Karolina ma o 25% wyższy wynik z egzaminu próbnego od Oli. Wynika z tego, że Oli wynik jest niższy od wyniku Karoliny o
A) 25% B) 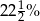 C) 20% D)
C) 20% D) 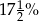
Granice 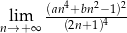 i
i 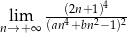 są równe. Stąd wynika, że
są równe. Stąd wynika, że
A) 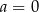 i
i 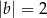 B)
B) 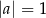 i
i 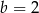 C)
C) 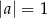 i
i 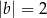 D)
D) 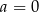 i
i 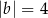
Wskaż równanie, którego rozwiązaniami są liczby 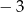 oraz 5.
oraz 5.
A) 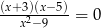 B)
B) 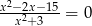 C)
C) 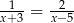 D)
D) 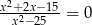
Wskaż równanie, którego rozwiązaniami są liczby 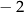 oraz 3.
oraz 3.
A) 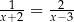 B)
B) 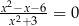 C)
C) 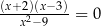 D)
D) 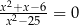
Ile jest wszystkich liczb naturalnych dodatnich mniejszych od 2021, których cyfra jedności jest jedną z cyfr: 0, 2, 6, 8?
A) 1010 B) 808 C) 606 D) 560
Dany jest kąt o mierze  taki, że
taki, że 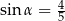 oraz
oraz 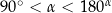 . Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Dla kąta o mierze  spełnione jest równanie: spełnione jest równanie: 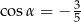 . . | P | F |
Dla kąta o mierze  spełnione jest równanie: spełnione jest równanie: 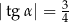 . . | P | F |
Objętość sześcianu 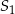 jest równa
jest równa 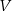 , a objętość sześcianu
, a objętość sześcianu 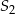 jest równa
jest równa 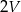 . Pole powierzchni całkowitej sześcianu
. Pole powierzchni całkowitej sześcianu 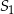 jest równe
jest równe 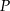 . Pole powierzchni całkowitej sześcianu
. Pole powierzchni całkowitej sześcianu 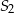 jest równe
jest równe
A) 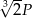 , , | B) 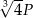 , , |
| ponieważ stosunek pól powierzchni brył podobnych jest równy | |
| 1) | sześcianowi skali podobieństwa. |
| 2) | skali podobieństwa. |
| 3) | kwadratowi skali podobieństwa. |
W trójkącie równoramiennym miara kąta przy podstawie jest równa 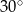 , a ramię ma długość 8 cm. Podstawa tego trójkąta ma długość
, a ramię ma długość 8 cm. Podstawa tego trójkąta ma długość
A) 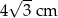 B) 4 cm C)
B) 4 cm C) 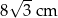 D)
D) 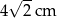
Ramię trójkąta równoramiennego ma długość 12 i tworzy z podstawą kąt o mierze 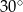 . Obwód tego trójkąta jest równy:
. Obwód tego trójkąta jest równy:
A) 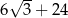 B) 30 C) 36 D)
B) 30 C) 36 D) 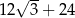
Miejscem zerowym funkcji
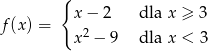
jest liczba
A) -3 B) 3 C) 2 D) 9
Miejscem zerowym funkcji
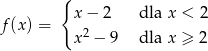
jest liczba
A) -3 B) 3 C) 2 D) 9
Funkcja określona wzorem
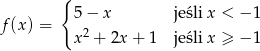
A) nie ma miejsc zerowych
B) ma tylko jedno miejsce zerowe
C) ma tylko dwa miejsca zerowe
D) ma trzy miejsca zerowe.
Funkcja
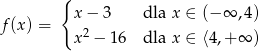
A) nie ma miejsc zerowych
B) ma dwa miejsce zerowe
C) ma jedno miejsca zerowe
D) ma trzy miejsca zerowe.

