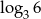Największą liczbą całkowitą spełniającą nierówność 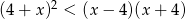 jest
jest
A) 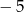 B)
B) 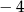 C)
C) 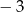 D)
D) 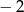
/Szkoła średnia/Zadania testowe
Wierzchołek paraboli o równaniu 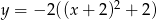 ma współrzędne
ma współrzędne
A) 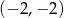 B)
B) 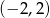 C)
C) 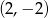 D)
D) 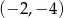
Wierzchołek paraboli o równaniu 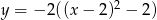 ma współrzędne
ma współrzędne
A) 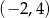 B)
B) 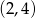 C)
C) 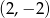 D)
D) 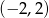
Punkt 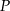 jest punktem wspólnym środkowych
jest punktem wspólnym środkowych 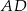 i
i 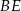 w trójkącie
w trójkącie 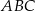 . Wówczas odcinki
. Wówczas odcinki 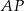 i
i 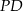 mogą mieć długości
mogą mieć długości
A) 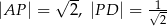 B)
B) 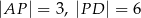
C) 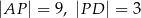 D)
D) 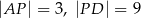
W klasie Ia jest o 25% więcej uczniów niż w klasie Ib. Stąd wynika, że w klasie Ib jest mniej uczniów niż w klasie Ia o
A) 25% B) 75% C) 20% D) 50%
Dane są punkty 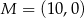 ,
, 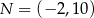 oraz
oraz 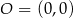 . Tangens kąta rozwartego
. Tangens kąta rozwartego 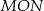 jest równy
jest równy
A) 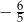 B)
B) 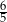 C) 1 D)
C) 1 D) 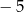
Iloraz ciągu geometrycznego 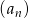 o wyrazie ogólnym
o wyrazie ogólnym 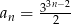 jest równy
jest równy
A) 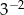 B)
B) 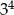 C)
C) 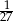 D) 27
D) 27
Ciąg geometryczny 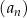 jest określony wzorem
jest określony wzorem 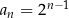 , dla każdej liczby naturalnej
, dla każdej liczby naturalnej 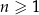 . Iloraz tego ciągu jest równy
. Iloraz tego ciągu jest równy
A) 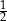 B)
B) 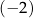 C) 2 D) 1
C) 2 D) 1
Ciąg geometryczny 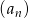 określony jest wzorem
określony jest wzorem 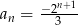 . Iloraz tego ciągu jest równy
. Iloraz tego ciągu jest równy
A) 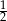 B)
B) 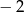 C)
C) 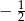 D) 2
D) 2
Ciąg geometryczny 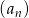 określony jest wzorem
określony jest wzorem 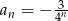 dla
dla 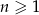 . Iloraz tego ciągu jest równy
. Iloraz tego ciągu jest równy
A) 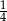 B)
B) 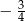 C)
C)  D)
D) 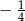
Ciąg geometryczny 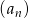 określony jest wzorem
określony jest wzorem 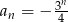 dla
dla 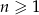 . Iloraz tego ciągu jest równy
. Iloraz tego ciągu jest równy
A) 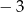 B)
B) 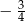 C)
C)  D) 3
D) 3
Iloraz ciągu geometrycznego 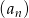 o wyrazie ogólnym
o wyrazie ogólnym 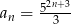 jest równy
jest równy
A) 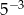 B)
B) 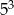 C) 25 D)
C) 25 D) 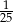
Obwód podstawy stożka wynosi 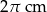 . Tworząca stożka jest 6 razy większa od promienia podstawy. Zatem pole powierzchni bocznej tego stożka jest równe
. Tworząca stożka jest 6 razy większa od promienia podstawy. Zatem pole powierzchni bocznej tego stożka jest równe
A) 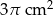 B)
B) 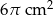 C)
C) 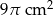 D)
D) 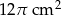
Obwód podstawy stożka wynosi 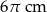 . Tworząca stożka jest 4 razy dłuższa od jego promienia podstawy. Zatem pole powierzchni całkowitej tego stożka jest równe
. Tworząca stożka jest 4 razy dłuższa od jego promienia podstawy. Zatem pole powierzchni całkowitej tego stożka jest równe
A) 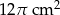 B)
B) 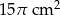 C)
C) 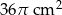 D)
D) 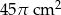
W słoiku w kształcie walca o średnicy 10 cm mieści się 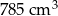 soku. Jeżeli przyjmiemy, że
soku. Jeżeli przyjmiemy, że 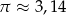 to wysokość słoika jest w przybliżeniu równa
to wysokość słoika jest w przybliżeniu równa
A) 2,5 cm B) 50 cm C) 25 cm D) 10 cm
W kubku w kształcie walca o średnicy 8 cm mieści się 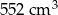 wody. Jeżeli przyjmiemy, że
wody. Jeżeli przyjmiemy, że 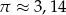 to wysokość kubka jest w przybliżeniu równa
to wysokość kubka jest w przybliżeniu równa
A) 2,7 cm B) 44 cm C) 11 cm D) 10 cm
W puszce w kształcie walca o średnicy 12 cm mieści się 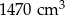 soku. Jeżeli przyjmiemy, że
soku. Jeżeli przyjmiemy, że 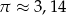 to wysokość puszki jest w przybliżeniu równa
to wysokość puszki jest w przybliżeniu równa
A) 13 cm B) 3,25 cm C) 26 cm D) 6,5 cm
Liczba 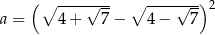 jest równa
jest równa
A) 2 B) 5 C) 8 D) 14
Liczba 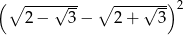 jest równa
jest równa
A) 2 B) 4 C) 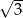 D)
D) 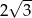
Liczba 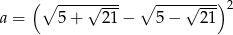 jest równa
jest równa
A) 4 B) 6 C) 10 D) 14
Liczba 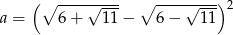 jest równa
jest równa
A) 22 B) 5 C) 8 D) 2
Liczba 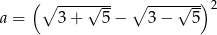 jest równa
jest równa
A) 2 B) 5 C) 8 D) 10
Przekrój osiowy stożka jest trójkątem równobocznym o boku  . Jeżeli
. Jeżeli  oznacza promień podstawy stożka,
oznacza promień podstawy stożka, 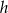 oznacza wysokość, to
oznacza wysokość, to
A) 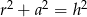 B)
B) 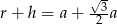 C)
C) 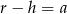 D)
D) 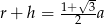
Przekrój osiowy stożka jest trójkątem równobocznym o wysokości 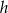 . Jeżeli
. Jeżeli  oznacza promień podstawy stożka,
oznacza promień podstawy stożka, 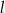 oznacza długość jego tworzącej, to
oznacza długość jego tworzącej, to
A) 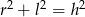 B)
B) 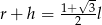 C)
C) 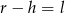 D)
D) 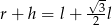
Ile rozwiązań posiada równanie 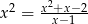 ?
?
A) 0 B) 1 C) 2 D) 3
Suma dwóch liczb niewymiernych
A) może być liczbą całkowitą B) nie może być liczbą całkowitą
C) jest zawsze liczbą niewymierną D) nie może być liczbą wymierną
Które z poniższych zdań jest prawdziwe?
A) Liczba przeciwna do liczby wymiernej jest liczbą niewymierną
B) Liczba 1 jest jednocześnie liczbą wymierną i niewymierną
C) Odwrotność każdej liczby całkowitej jest liczbą całkowitą
D) Liczba 0 jest liczbą wymierną
Różnica dwóch liczb niewymiernych
A) nie może być liczbą wymierną B) nie może być liczbą całkowitą
C) jest zawsze liczbą niewymierną D) może być liczbą całkowitą
Iloczyn dwóch liczb niewymiernych
A) nie może być liczbą całkowitą B) może być liczbą całkowitą
C) jest zawsze liczbą niewymierną D) nie może być liczbą wymierną
Przekrój osiowy stożka jest trójkątem rozwartokątnym o polu 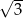 . Jeżeli tworząca tego stożka ma długość 2, to jego objętość jest równa
. Jeżeli tworząca tego stożka ma długość 2, to jego objętość jest równa
A) 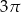 B)
B) 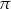 C)
C) 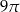 D)
D) 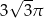
Na okręgu opisanym na kwadracie 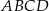 wybrano punkt
wybrano punkt 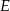 w ten sposób, że
w ten sposób, że 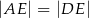 .
.
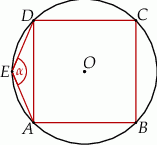
Miara kąta oznaczonego na rysunku literą  jest równa
jest równa
A) 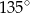 B)
B) 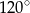 C)
C) 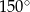 D)
D) 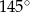
Boki prostokąta mają długości 5 i 12. Sinus kąta pod jakim przecinają się przekątne tego prostokąta jest równy
A) 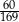 B)
B) 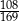 C)
C) 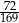 D)
D) 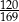
Liczba 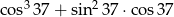 jest równa
jest równa
A) 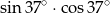 B)
B) 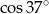 C)
C) 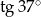 D)
D) 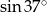
Liczba 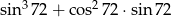 jest równa
jest równa
A) 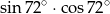 B)
B) 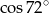 C)
C) 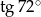 D)
D) 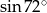
Liczba 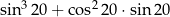 jest równa
jest równa
A) 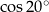 B)
B) 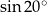 C)
C) 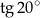 D)
D) 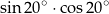
Funkcja wykładnicza określona wzorem 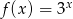 przyjmuje wartość 6 dla argumentu
przyjmuje wartość 6 dla argumentu
A) 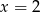 B)
B) 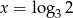 C)
C) 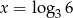 D)
D) 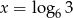
Funkcja wykładnicza określona wzorem 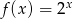 przyjmuje wartość 3 dla argumentu
przyjmuje wartość 3 dla argumentu
A) 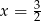 B)
B) 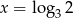 C)
C) 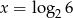 D)
D) 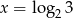
Na rysunku przedstawiony jest fragment paraboli będącej wykresem funkcji kwadratowej 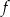 . Wierzchołkiem tej paraboli jest punkt
. Wierzchołkiem tej paraboli jest punkt 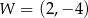 . Liczby 0 i 4 to miejsca zerowe funkcji
. Liczby 0 i 4 to miejsca zerowe funkcji 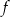 .
.
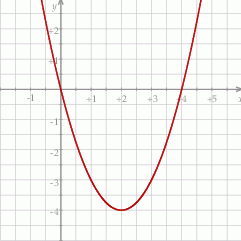
Osią symetrii wykresu funkcji 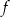 jest prosta o równaniu
jest prosta o równaniu
A) 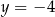 B)
B) 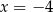 C)
C) 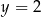 D)
D) 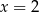
Funkcja kwadratowa 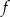 jest określona wzorem
jest określona wzorem 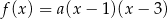 . Na rysunku przedstawiono fragment paraboli będącej wykresem tej funkcji. Wierzchołkiem tej paraboli jest punkt
. Na rysunku przedstawiono fragment paraboli będącej wykresem tej funkcji. Wierzchołkiem tej paraboli jest punkt 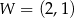 .
.
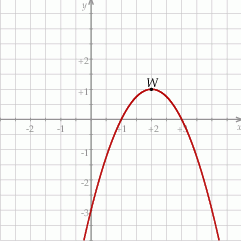
Osią symetrii paraboli będącej wykresem funkcji 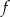 jest prosta o równaniu
jest prosta o równaniu
A) 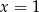 B)
B) 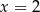 C)
C) 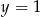 D)
D) 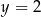
W kartezjańskim układzie współrzędnych 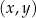 przedstawiono fragment paraboli, która jest wykresem funkcji kwadratowej
przedstawiono fragment paraboli, która jest wykresem funkcji kwadratowej 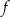 (zobacz rysunek). Wierzchołek tej paraboli oraz punkty przecięcia paraboli z osią
(zobacz rysunek). Wierzchołek tej paraboli oraz punkty przecięcia paraboli z osią 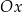 układu współrzędnych mają obie współrzędne całkowite.
układu współrzędnych mają obie współrzędne całkowite.
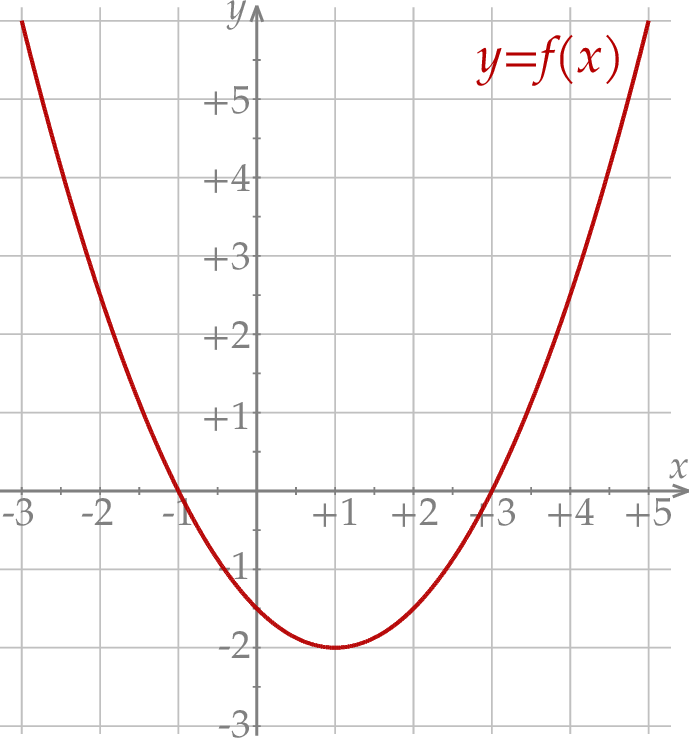
Osią symetrii wykresu funkcji 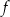 jest prosta o równaniu
jest prosta o równaniu
A) 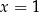 B)
B) 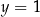 C)
C) 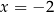 D)
D) 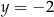
Na rysunku przedstawiony jest fragment paraboli będącej wykresem funkcji kwadratowej 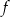 . Wierzchołkiem tej paraboli jest punkt
. Wierzchołkiem tej paraboli jest punkt 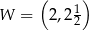 . Liczby
. Liczby 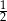 i
i 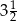 to miejsca zerowe funkcji
to miejsca zerowe funkcji 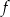 .
.
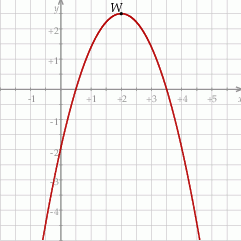
Osią symetrii wykresu funkcji 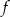 jest prosta o równaniu
jest prosta o równaniu
A) 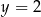 B)
B) 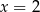 C)
C) 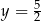 D)
D) 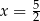
Funkcja kwadratowa 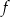 jest określona wzorem
jest określona wzorem 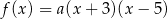 . Na rysunku przedstawiono fragment paraboli będącej wykresem tej funkcji. Wierzchołkiem tej paraboli jest punkt
. Na rysunku przedstawiono fragment paraboli będącej wykresem tej funkcji. Wierzchołkiem tej paraboli jest punkt 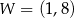 .
.
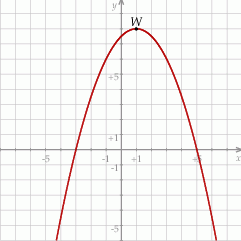
Osią symetrii paraboli będącej wykresem funkcji 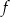 jest prosta o równaniu
jest prosta o równaniu
A) 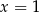 B)
B) 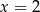 C)
C) 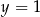 D)
D) 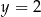
W pudełku znajduje się 5 kartek, na których zapisano wszystkie możliwe jednocyfrowe liczby naturalne nieparzyste. Wyjmujemy z pudełka kolejno trzy kartki i układając je jedna obok drugiej tworzymy liczby trzycyfrowe. Liczb takich możemy utworzyć maksymalnie
A) 120 B) 125 C) 60 D) 15
W pudełku znajduje się 5 kartek, na których zapisano liczby: 0, 2, 4, 6, 8. Wyjmujemy z pudełka kolejno trzy kartki i układając je jedna obok drugiej tworzymy liczby trzycyfrowe. Liczb takich możemy utworzyć maksymalnie
A) 48 B) 125 C) 100 D) 60
Liczba 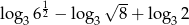 jest równa
jest równa
A) 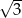 B)
B) 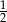 C)
C) 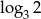 D)
D)