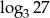Wskaż nierówność, która opisuje sumę przedziałów zaznaczonych na osi liczbowej.
![]()
A) 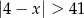 B)
B) 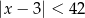 C)
C) 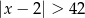 D)
D) 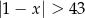
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Wskaż nierówność, która opisuje sumę przedziałów zaznaczonych na osi liczbowej.
![]()
A) 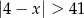 B)
B) 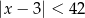 C)
C) 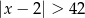 D)
D) 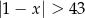
Wskaż nierówność, która opisuje sumę przedziałów zaznaczonych na osi liczbowej.
![]()
A) 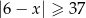 B)
B) 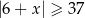 C)
C) 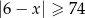 D)
D) 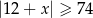
Wskaż nierówność, która opisuje sumę przedziałów zaznaczonych na osi liczbowej.

A) 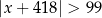 B)
B) 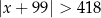 C)
C) 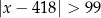 D)
D) 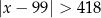
Diagram przedstawia ile procent rodzin mieszkających w jednym z łódzkich bloków posiada 0,1,2,3 lub 4 dzieci.
Średnia liczba dzieci przypadających na jedną rodzinę jest równa
A) 1,22 B) 1,44 C) 2 D) 2,5
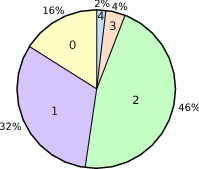
Diagram przedstawia ile procent mieszkańców pewnego osiedla było w listopadzie w kinie 0,1,2,3 lub 4 razy. Średnia liczba wyjść do kina w listopadzie przypadających na jednego mieszkańca jest równa
A) 1,3 B) 1,44 C) 2 D) 2,5
Dany jest okrąg o środku w punkcie 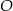 . Prosta
. Prosta 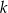 jest styczna do okręgu w punkcie
jest styczna do okręgu w punkcie 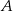 .
.
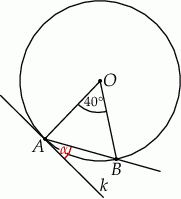
Miara kąta 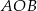 wynosi
wynosi 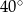 . Wobec tego miara kąta
. Wobec tego miara kąta  jest równa
jest równa
A) 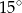 B)
B) 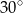 C)
C) 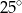 D)
D) 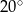
W okręgu o środku 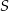 zaznaczono kąt oparty na łuku
zaznaczono kąt oparty na łuku 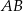 . Przez punkt
. Przez punkt 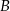 poprowadzono prostą
poprowadzono prostą 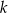 styczną do okręgu.
styczną do okręgu.
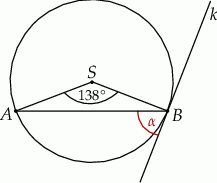
Zaznaczony na rysunku kąt  zawarty między styczną
zawarty między styczną 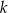 i cięciwą
i cięciwą 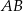 ma miarę
ma miarę
A) 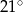 B)
B) 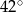 C)
C) 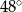 D)
D) 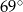
Punkty 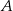 oraz
oraz 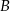 leżą na okręgu o środku
leżą na okręgu o środku 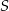 . Kąt środkowy
. Kąt środkowy 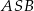 ma miarę
ma miarę 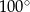 . Prosta
. Prosta 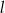 jest styczna do tego okręgu w punkcie
jest styczna do tego okręgu w punkcie 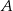 i tworzy z cięciwą
i tworzy z cięciwą 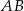 okręgu kąt o mierze
okręgu kąt o mierze  (zobacz rysunek).
(zobacz rysunek).
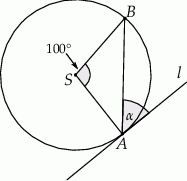
Wtedy
A) 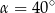 B)
B) 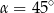 C)
C) 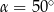 D)
D) 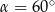
Dany jest okrąg o środku w punkcie 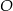 . Prosta
. Prosta 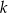 jest styczna do okręgu w punkcie
jest styczna do okręgu w punkcie 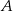 .
.
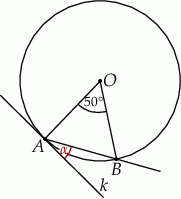
Miara kąta 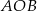 wynosi
wynosi 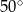 . Wobec tego miara kąta
. Wobec tego miara kąta  jest równa
jest równa
A) 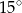 B)
B) 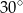 C)
C) 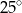 D)
D) 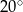
W okręgu o środku 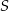 zaznaczono kąt oparty na łuku
zaznaczono kąt oparty na łuku 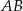 . Przez punkt
. Przez punkt 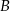 poprowadzono prostą
poprowadzono prostą 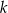 styczną do okręgu.
styczną do okręgu.
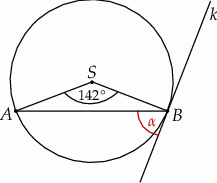
Zaznaczony na rysunku kąt  zawarty między styczną
zawarty między styczną 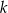 i cięciwą
i cięciwą 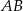 ma miarę
ma miarę
A) 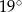 B)
B) 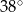 C)
C) 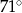 D)
D) 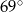
Dany jest okrąg o środku w punkcie 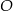 . Prosta
. Prosta 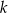 jest styczna do okręgu w punkcie
jest styczna do okręgu w punkcie  .
.
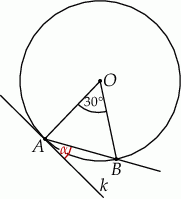
Miara kąta 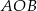 wynosi
wynosi 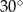 . Wobec tego miara kąta
. Wobec tego miara kąta  jest równa
jest równa
A) 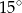 B)
B) 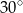 C)
C) 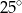 D)
D) 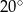
Jeśli 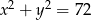 i
i 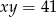 , to kwadrat sumy liczb
, to kwadrat sumy liczb 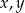 jest równy
jest równy
A) 6865 B) 154 C) 113 D) 5184
Jeśli 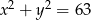 i
i 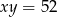 , to kwadrat sumy liczb
, to kwadrat sumy liczb 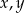 jest równy
jest równy
A) 167 B) 3969 C) 115 D) 4073
Jeśli 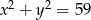 i
i 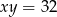 , to kwadrat sumy liczb
, to kwadrat sumy liczb 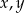 jest równy
jest równy
A) 3545 B) 91 C) 123 D) 3481
Funkcja 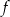 jest określona wzorem
jest określona wzorem 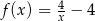 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej 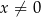 . Liczba
. Liczba 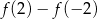 jest równa
jest równa
A) 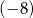 B)
B) 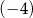 C) 4 D) 0
C) 4 D) 0
Dany jest trójkąt równoboczny, którego pole jest równe 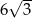 . Bok tego trójkąta ma długość
. Bok tego trójkąta ma długość
A) 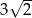 B)
B) 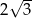 C)
C) 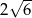 D)
D) 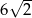
Pole pewnego trójkąta równobocznego jest równe 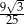 . Obwód tego trójkąta jest równy
. Obwód tego trójkąta jest równy
A) 4 B) 2 C) 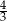 D)
D) 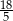
Dany jest trójkąt równoboczny, którego pole jest równe 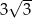 . Bok tego trójkąta ma długość
. Bok tego trójkąta ma długość
A) 3 B) 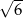 C) 6 D)
C) 6 D) 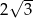
Pole pewnego trójkąta równobocznego jest równe 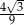 . Obwód tego trójkąta jest równy
. Obwód tego trójkąta jest równy
A) 4 B) 2 C) 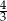 D)
D) 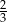
Wyrażenie 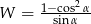 można zapisać w postaci
można zapisać w postaci
A) 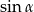 B)
B) 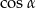 C)
C) 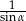 D) 1
D) 1
Wyrażenie 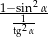 , gdzie
, gdzie  jest kątem ostrym, można zapisać w postaci
jest kątem ostrym, można zapisać w postaci
A) 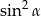 B)
B) 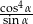 C)
C) 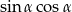 D)
D) 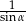
Wyrażenie 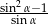 dla kąta ostrego
dla kąta ostrego  jest równe
jest równe
A) 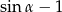 B)
B) 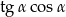 C)
C) 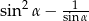 D)
D) 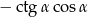
Wyrażenie 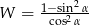 można zapisać w postaci
można zapisać w postaci
A) 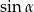 B)
B) 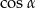 C)
C) 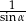 D) 1
D) 1
Wyrażenie 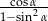 można zapisać w postaci:
można zapisać w postaci:
A) 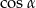 B)
B) 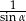 C)
C) 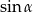 D)
D) 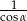
Wyrażenie 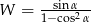 można zapisać w postaci
można zapisać w postaci
A) 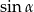 B)
B) 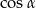 C)
C) 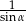 D) 1
D) 1
Dany jest trójkąt prostokątny o długościach boków 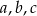 , gdzie
, gdzie 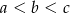 . Obracając ten trójkąt, wokół prostej zawierającej dłuższą przyprostokątną o kąt
. Obracając ten trójkąt, wokół prostej zawierającej dłuższą przyprostokątną o kąt 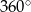 , otrzymujemy bryłę, której objętość jest równa
, otrzymujemy bryłę, której objętość jest równa
A) 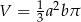 B)
B) 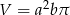 C)
C) 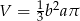 D)
D) 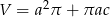
Dany jest trójkąt prostokątny o długościach boków 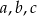 , gdzie
, gdzie 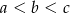 . Obracając ten trójkąt, wokół prostej zawierającej krótszą przyprostokątną o kąt
. Obracając ten trójkąt, wokół prostej zawierającej krótszą przyprostokątną o kąt 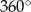 , otrzymujemy bryłę, której objętość jest równa
, otrzymujemy bryłę, której objętość jest równa
A) 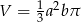 B)
B) 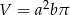 C)
C) 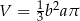 D)
D) 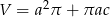
Liczba 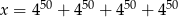 jest równa liczbie
jest równa liczbie
A) 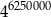 B)
B) 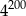 C)
C) 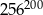 D)
D) 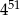
Suma 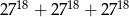 jest równa
jest równa
A) 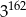 B)
B) 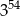 C)
C) 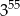 D)
D) 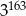
Suma 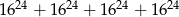 jest równa
jest równa
A) 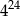 B)
B) 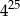 C)
C) 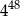 D)
D) 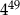
Sumę liczb 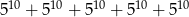 można przedstawić w postaci
można przedstawić w postaci
A) 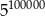 B)
B) 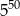 C)
C) 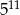 D)
D) 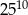
Liczba 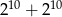 jest równa.
jest równa.
A) 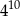 B)
B) 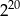 C)
C) 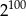 D)
D) 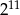
Liczba 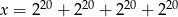 jest równa liczbie
jest równa liczbie
A) 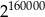 B)
B) 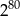 C)
C) 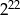 D)
D) 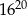
Liczba 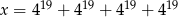 jest równa liczbie
jest równa liczbie
A) 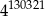 B)
B) 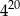 C)
C) 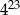 D)
D) 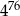
Liczba 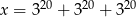 jest równa liczbie
jest równa liczbie
A) 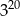 B)
B) 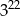 C)
C) 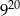 D)
D) 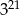
Funkcja 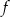 ma dwa miejsca zerowe 3 oraz
ma dwa miejsca zerowe 3 oraz 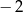 . Zatem funkcja
. Zatem funkcja 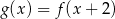
A) ma dwa miejsca zerowe 5 oraz 0 B) ma dwa miejsca zerowe 1 oraz 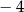
C) ma dwa miejsca zerowe 4 oraz 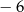 D) nie ma miejsc zerowych
D) nie ma miejsc zerowych
Funkcja 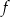 ma dwa miejsca zerowe 3 oraz
ma dwa miejsca zerowe 3 oraz 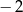 . Zatem funkcja
. Zatem funkcja 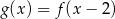
A) ma dwa miejsca zerowe 5 oraz 0 B) ma dwa miejsca zerowe 1 oraz 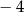
C) ma dwa miejsca zerowe 4 oraz 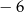 D) nie ma miejsc zerowych
D) nie ma miejsc zerowych
Kąt nachylenia ściany bocznej ostrosłupa prawidłowego czworokątnego do płaszczyzny podstawy ma miarę 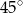 . Krawędź podstawy ma długość 6 cm. Długość wysokości tego ostrosłupa jest równa
. Krawędź podstawy ma długość 6 cm. Długość wysokości tego ostrosłupa jest równa
A) 6 cm B) 3 cm C) 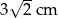 D)
D) 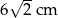
Kąt nachylenia ściany bocznej ostrosłupa prawidłowego czworokątnego do płaszczyzny podstawy ma miarę 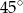 . Wysokość ściany bocznej ma długość 6 cm. Długość wysokości tego ostrosłupa jest równa
. Wysokość ściany bocznej ma długość 6 cm. Długość wysokości tego ostrosłupa jest równa
A) 6 cm B) 3 cm C) 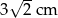 D)
D) 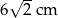
Kąt nachylenia krawędzi bocznej ostrosłupa prawidłowego czworokątnego do płaszczyzny podstawy ma miarę 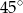 . Krawędź boczna ma długość 12 cm. Długość wysokości tego ostrosłupa jest równa
. Krawędź boczna ma długość 12 cm. Długość wysokości tego ostrosłupa jest równa
A) 6 cm B) 3 cm C) 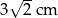 D)
D) 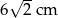
Liczba 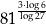 jest równa
jest równa
A) 6561 B) 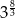 C) 1296 D)
C) 1296 D) 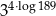
Jednym z miejsc zerowych funkcji kwadratowej 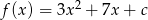 jest liczba
jest liczba 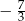 . Wówczas
. Wówczas  jest równe
jest równe
A) 0 B) 1 C) 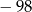 D) 98
D) 98
Jednym z miejsc zerowych funkcji kwadratowej 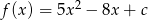 jest liczba
jest liczba  . Wówczas
. Wówczas  jest równe
jest równe
A) 1 B) 0 C) 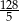 D)
D) 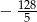
Dane są punkty 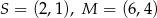 . Równanie okręgu o środku
. Równanie okręgu o środku 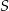 i przechodzącego przez punkt
i przechodzącego przez punkt 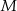 ma postać
ma postać
A) 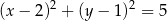 B)
B) 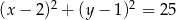
C) 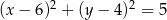 D)
D) 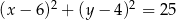
Dane są punkty 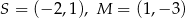 . Równanie okręgu o środku
. Równanie okręgu o środku 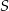 i przechodzącego przez punkt
i przechodzącego przez punkt 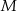 ma postać
ma postać
A) 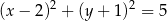 B)
B) 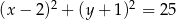
C) 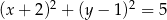 D)
D) 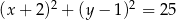
Niech 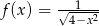 . Dziedziną funkcji
. Dziedziną funkcji 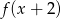 jest zbiór
jest zbiór
A) 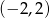 B)
B) 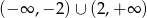 C)
C) 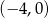 D)
D) 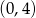
Funkcja liniowa 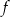 jest określona wzorem
jest określona wzorem 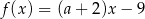 , gdzie
, gdzie  to pewna liczba rzeczywista. Wykres funkcji
to pewna liczba rzeczywista. Wykres funkcji 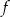 nie ma punktów wspólnych z prostą
nie ma punktów wspólnych z prostą 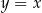 . Stąd wynika, że
. Stąd wynika, że
A) 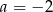 B)
B) 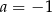 C)
C) 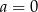 D)
D) 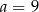
Pole koła ograniczonego okręgiem 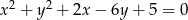 jest równe
jest równe
A) 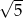 B)
B) 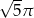 C)
C) 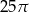 D)
D) 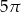
Wiadomo, że wielomian 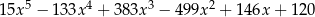 ma w zbiorze
ma w zbiorze 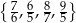 dokładnie jeden pierwiastek wymierny. Jest nim liczba
dokładnie jeden pierwiastek wymierny. Jest nim liczba
A) 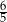 B)
B)  C)
C) 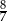 D)
D) 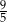
Wiadomo, że wielomian 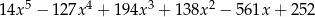 ma w zbiorze
ma w zbiorze 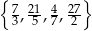 dokładnie jeden pierwiastek wymierny. Jest nim liczba
dokładnie jeden pierwiastek wymierny. Jest nim liczba
A)  B)
B) 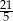 C)
C) 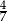 D)
D) 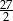
Wskaż 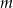 , dla którego miejsce zerowe funkcji liniowej
, dla którego miejsce zerowe funkcji liniowej 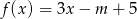 jest liczbą z przedziału
jest liczbą z przedziału 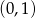 .
.
A) 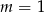 B)
B) 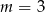 C)
C) 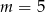 D)
D) 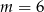
Wskaż 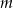 , dla którego miejsce zerowe funkcji liniowej
, dla którego miejsce zerowe funkcji liniowej 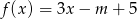 jest liczbą z przedziału
jest liczbą z przedziału 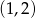 .
.
A) 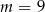 B)
B) 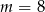 C)
C) 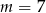 D)
D) 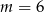
Która z liczb jest równa 2?
A) 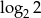 B)
B) 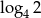 C)
C) 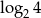 D)
D) 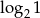
Która z liczb jest równa 3?
A) 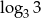 B)
B) 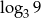 C)
C) 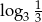 D)
D)