Dany jest wielomian 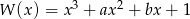 , gdzie
, gdzie  i
i 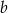 są liczbami całkowitymi. Zatem
są liczbami całkowitymi. Zatem
A) Równanie 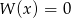 musi mieć co najmniej 2 różne pierwiastki.
musi mieć co najmniej 2 różne pierwiastki.
B) Jeżeli równanie 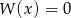 ma pierwiastek całkowity, to
ma pierwiastek całkowity, to 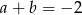 .
.
C) Jeżeli równanie 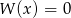 ma ujemny pierwiastek wymierny, to
ma ujemny pierwiastek wymierny, to 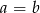 .
.
D) Równanie 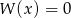 może nie mieć rozwiązań.
może nie mieć rozwiązań.
/Szkoła średnia/Zadania testowe
Dany jest wielomian 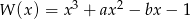 , gdzie
, gdzie  i
i 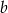 są liczbami całkowitymi. Zatem
są liczbami całkowitymi. Zatem
A) Jeżeli równanie 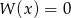 ma pierwiastek wymierny, to
ma pierwiastek wymierny, to 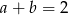 .
.
B) Jeżeli równanie 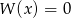 ma dodatni pierwiastek całkowity, to
ma dodatni pierwiastek całkowity, to 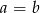 .
.
C) Równanie 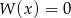 może nie mieć rozwiązań.
może nie mieć rozwiązań.
D) Równanie 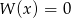 musi mieć co najmniej 2 różne pierwiastki.
musi mieć co najmniej 2 różne pierwiastki.
Dany jest wielomian 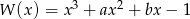 , gdzie
, gdzie  i
i 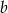 są liczbami całkowitymi. Zatem
są liczbami całkowitymi. Zatem
A) Jeżeli równanie 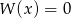 ma pierwiastek wymierny, to
ma pierwiastek wymierny, to 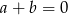 .
.
B) Jeżeli równanie 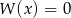 ma ujemny pierwiastek całkowity, to
ma ujemny pierwiastek całkowity, to 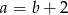 .
.
C) Równanie 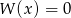 może nie mieć rozwiązań.
może nie mieć rozwiązań.
D) Równanie 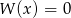 musi mieć co najmniej 2 różne pierwiastki.
musi mieć co najmniej 2 różne pierwiastki.
Dany jest czworokąt 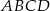 wpisany w okrąg o środku
wpisany w okrąg o środku 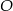 . Wówczas, jeśli
. Wówczas, jeśli 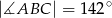 , to miara kąta
, to miara kąta 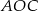 jest równa
jest równa
A) 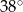 B)
B) 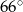 C)
C) 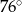 D)
D) 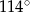
Dany jest czworokąt 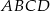 wpisany w okrąg o środku
wpisany w okrąg o środku  . Wówczas, jeśli
. Wówczas, jeśli 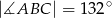 , to miara kąta
, to miara kąta 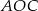 jest równa
jest równa
A) 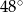 B)
B) 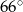 C)
C) 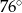 D)
D) 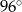
Dany jest czworokąt 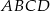 wpisany w okrąg o środku
wpisany w okrąg o środku 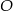 . Wówczas, jeśli
. Wówczas, jeśli 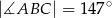 , to miara kąta
, to miara kąta 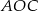 jest równa
jest równa
A) 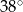 B)
B) 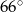 C)
C) 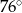 D)
D) 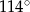
Liczba 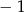 jest miejscem zerowym funkcji
jest miejscem zerowym funkcji 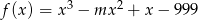 . Zatem
. Zatem
A) 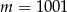 B)
B) 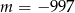 C)
C) 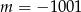 D)
D) 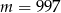
Liczba 5 jest pierwiastkiem wielomianu 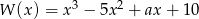 . Współczynnik
. Współczynnik  jest równy
jest równy
A) 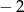 B)
B) 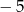 C) 2 D) 5
C) 2 D) 5
Liczba 2 jest pierwiastkiem wielomianu 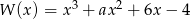 . Współczynnik
. Współczynnik  jest równy
jest równy
A) 2 B) -2 C) 4 D) -4
Liczba 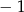 jest miejscem zerowym funkcji
jest miejscem zerowym funkcji 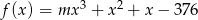 . Zatem
. Zatem
A) 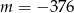 B)
B) 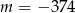 C)
C) 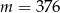 D)
D) 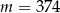
Dane są wielomiany 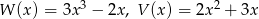 . Stopień wielomianu
. Stopień wielomianu 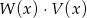 jest równy
jest równy
A) 6 B) 5 C) 4 D) 3
Dane są wielomiany: 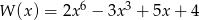 i
i 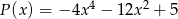 . Stopień wielomianu
. Stopień wielomianu 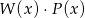 jest równy:
jest równy:
A) 24 B) 10 C) 9 D) 6
Dane są wielomiany: 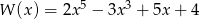 i
i 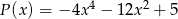 . Stopień wielomianu
. Stopień wielomianu 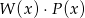 jest równy:
jest równy:
A) 20 B) -8 C) 9 D) 5
Dane są wielomiany 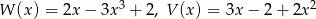 . Stopień wielomianu
. Stopień wielomianu 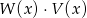 jest równy
jest równy
A) 6 B) 4 C) 5 D) 3
Iloczyn wielomianów 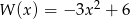 i
i 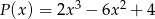 jest wielomianem stopnia
jest wielomianem stopnia
A) 2 B) 3 C) 5 D) 6
Iloczyn wielomianów 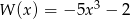 i
i 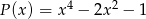 jest wielomianem stopnia
jest wielomianem stopnia
A) 7 B) 3 C) 5 D) 6
Dane są dwa wielomiany 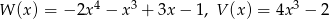 . Stopień wielomianu
. Stopień wielomianu 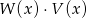 jest równy
jest równy
A) 12 B) 7 C) 4 D) 3
Wielomian 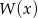 jest iloczynem wielomianów
jest iloczynem wielomianów 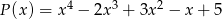 i
i 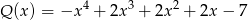 . Zatem stopień wielomianu
. Zatem stopień wielomianu 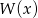 jest równy
jest równy
A) 16 B) 8 C) 4 D) 2
Prosta 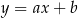 ma z jedną osią układu współrzędnych dokładnie jeden punkt wspólny. Z drugą osią układu współrzędnych nie ma punktów wspólnych. Zatem prosta ta
ma z jedną osią układu współrzędnych dokładnie jeden punkt wspólny. Z drugą osią układu współrzędnych nie ma punktów wspólnych. Zatem prosta ta
A) przecina tylko oś 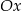 B) przechodzi przez początek układu współrzędnych
B) przechodzi przez początek układu współrzędnych
C) jest równoległa do osi 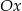 D) jest równoległa do osi
D) jest równoległa do osi 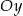
Punkty wspólne prostej 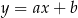 z osiami układu współrzędnych pokrywają się. Zatem prosta ta
z osiami układu współrzędnych pokrywają się. Zatem prosta ta
A) przecina tylko oś 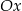 B) przechodzi przez początek układu współrzędnych
B) przechodzi przez początek układu współrzędnych
C) jest równoległa do osi 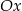 D) jest równoległa do osi
D) jest równoległa do osi 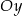
Dane są liczby 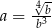 ,
, 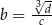 ,
, 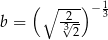 ,
, 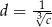 . Zatem
. Zatem
A) 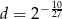 B)
B) 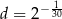 C)
C) 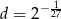 D)
D) 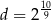
Liczba 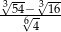 jest równa
jest równa
A) 2 B) 1 C) 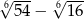 D)
D) 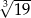
Liczba 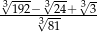 jest równa
jest równa
A) 1 B) 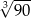 C)
C)  D)
D) 
Liczba 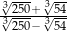 jest równa
jest równa
A) 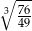 B)
B) 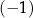 C) 4 D)
C) 4 D) 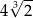
Cena pewnego towaru w wyniku obniżki o 10% zmniejszyła się o 2 018 zł. Ten towar po tej obniżce kosztował
A) 20 180 zł B) 18 162 zł C) 2 108 zł D) 2 028 zł
Funkcja 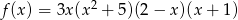 ma dokładnie
ma dokładnie
A) 1 pierwiastek B) 2 pierwiastki C) 3 pierwiastki D) 4 pierwiastki
Funkcja 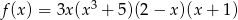 ma dokładnie
ma dokładnie
A) 1 pierwiastek B) 2 pierwiastki C) 3 pierwiastki D) 4 pierwiastki
Liczba 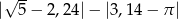 jest równa
jest równa
A) 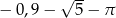 B)
B) 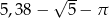 C)
C) 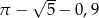 D)
D) 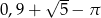
Liczba 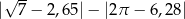 jest równa
jest równa
A) 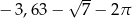 B)
B) 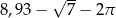 C)
C) 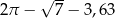 D)
D) 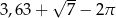
Ile rozwiązań ma układ równań 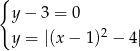
A) 1 B) 2 C) 3 D) 4
Miejscami zerowymi funkcji kwadratowej 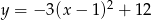 są
są
A) 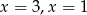 B)
B) 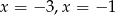 C)
C) 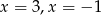 D)
D) 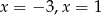
Miejscami zerowymi funkcji kwadratowej 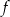 określonej wzorem
określonej wzorem 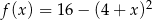 są liczby
są liczby
A) 0 oraz 4 B) 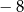 oraz 8 C) 0 oraz
oraz 8 C) 0 oraz 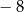 D)
D) 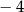 oraz 4
oraz 4
Miejscami zerowymi funkcji kwadratowej 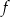 określonej wzorem
określonej wzorem 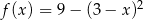 są liczby
są liczby
A) 0 oraz 3 B) 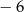 oraz 6 C) 0 oraz
oraz 6 C) 0 oraz 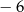 D) 0 oraz 6
D) 0 oraz 6
Funkcja 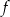 jest określona dla każdej liczby rzeczywistej
jest określona dla każdej liczby rzeczywistej  wzorem
wzorem 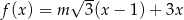 . Ta funkcja jest malejąca dla każdej liczby
. Ta funkcja jest malejąca dla każdej liczby 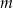 spełniającej warunek
spełniającej warunek
A) 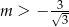 B)
B) 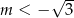 C)
C) 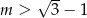 D)
D) 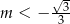
Funkcja 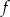 jest określona dla każdej liczby rzeczywistej
jest określona dla każdej liczby rzeczywistej  wzorem
wzorem 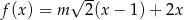 . Ta funkcja jest rosnąca dla każdej liczby
. Ta funkcja jest rosnąca dla każdej liczby 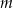 spełniającej warunek
spełniającej warunek
A) 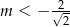 B)
B) 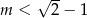 C)
C) 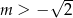 D)
D) 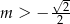
Jeżeli 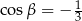 i
i 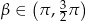 , to wartość wyrażenia
, to wartość wyrażenia 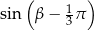 jest równa
jest równa
A) 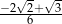 B)
B) 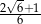 C)
C) 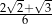 D)
D) 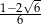
Funkcja liniowa określona jest wzorem 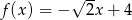 . Miejscem zerowym tej funkcji jest liczba
. Miejscem zerowym tej funkcji jest liczba
A) 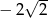 B)
B) 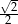 C)
C) 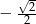 D)
D) 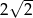
Funkcja liniowa określona jest wzorem 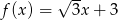 . Miejscem zerowym tej funkcji jest liczba
. Miejscem zerowym tej funkcji jest liczba
A) 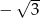 B)
B) 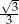 C)
C) 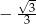 D)
D) 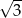
Miejscem zerowym funkcji liniowej 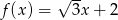 jest liczba:
jest liczba:
A) 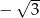 B) -2 C)
B) -2 C) 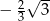 D)
D) 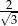
Miejscem zerowym funkcji 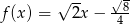 jest liczba:
jest liczba:
A) 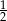 B)
B) 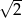 C)
C) 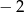 D) 2
D) 2
Ciąg 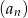 określony jest w następujący sposób
określony jest w następujący sposób 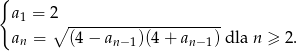 Setny wyraz ciągu
Setny wyraz ciągu 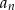 jest równy
jest równy
A) 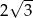 B) 2 C) 100 D)
B) 2 C) 100 D) 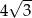
Jeżeli  jest kątem ostrym pod jakim przecinają się proste
jest kątem ostrym pod jakim przecinają się proste 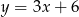 i
i 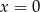 , to
, to
A) 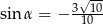 B)
B) 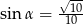 C)
C) 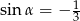 D)
D) 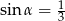
Dany jest prostopadłościan o wymiarach 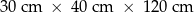 (zobacz rysunek), a ponadto dane są cztery odcinki
(zobacz rysunek), a ponadto dane są cztery odcinki 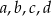 , o długościach – odpowiednio – 119 cm, 121 cm, 129 cm i 131 cm.
, o długościach – odpowiednio – 119 cm, 121 cm, 129 cm i 131 cm.
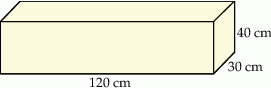
Przekątna tego prostopadłościanu jest dłuższa
A) tylko od odcinka  .
.
B) tylko od odcinków  i
i 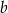 .
.
C) tylko od odcinków 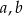 i
i  .
.
D) od wszystkich czterech danych odcinków.
Dany jest prostopadłościan o wymiarach 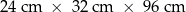 (zobacz rysunek), a ponadto dane są cztery odcinki
(zobacz rysunek), a ponadto dane są cztery odcinki 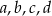 , o długościach – odpowiednio – 89 cm, 101 cm, 110 cm i 121 cm.
, o długościach – odpowiednio – 89 cm, 101 cm, 110 cm i 121 cm.
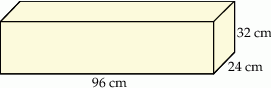
Przekątna tego prostopadłościanu jest dłuższa
A) tylko od odcinka  .
.
B) tylko od odcinków  i
i 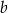 .
.
C) tylko od odcinków 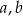 i
i  .
.
D) od wszystkich czterech danych odcinków.
Dane są liczby 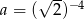 oraz
oraz 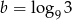 . Zatem
. Zatem
A) 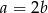 B)
B) 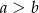 C)
C) 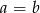 D)
D) 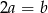
Jeżeli 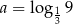 oraz
oraz 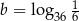 , to
, to
A) 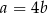 B)
B) 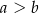 C)
C) 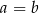 D)
D) 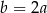
W poniższej tabeli zebrano zarobki wszystkich pracowników pewnej firmy handlowej.
| Imię pracownika | Zarobki |
| Kamila, Krzysztof, Stefan | 2800 zł |
| Zofia, Łukasz | 3000 zł |
| Ela, Marta | 3200 zł |
| Henryk | 3600 zł. |
Jaka jest średnia zarobków pracowników tej firmy?
A) 3050 zł B) 3150 zł C) 3200 zł D) 3250 zł

