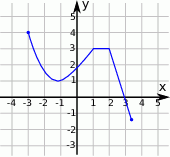
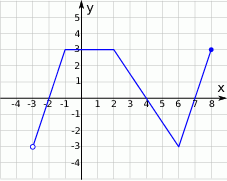
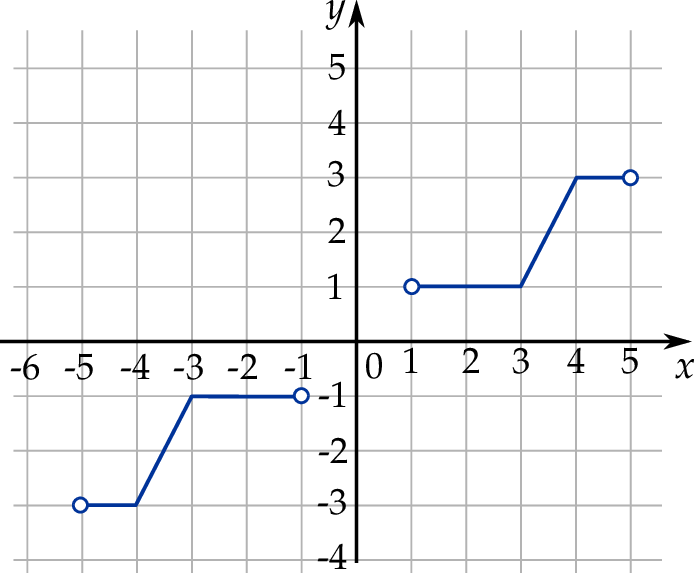
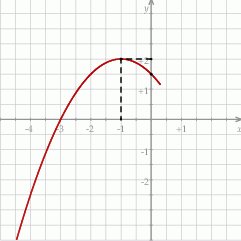
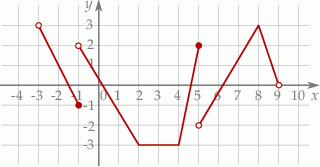
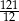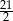Na rysunku przedstawiono wykres funkcji  określonej na zbiorze
określonej na zbiorze 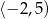 .
.
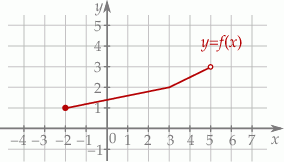
Funkcja 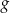 jest określona za pomocą funkcji
jest określona za pomocą funkcji 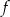 następująco:
następująco: 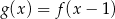 . Wykres funkcji
. Wykres funkcji 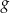 można otrzymać poprzez odpowiednie przesunięcie wykresu funkcji
można otrzymać poprzez odpowiednie przesunięcie wykresu funkcji 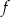 . Dziedziną funkcji
. Dziedziną funkcji 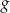 jest zbiór
jest zbiór
A) 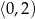 B)
B) 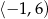 C)
C) 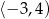 D)
D) 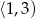

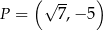 należy do wykresu funkcji
należy do wykresu funkcji 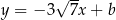 . Parametr
. Parametr 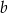 jest równy
jest równy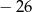
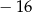
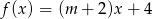 leży punkt
leży punkt 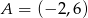 . Zatem
. Zatem 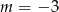
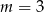
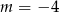
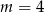
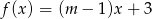 leży punkt
leży punkt 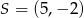 . Zatem
. Zatem 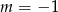
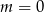
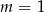
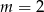
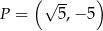 należy do wykresu funkcji
należy do wykresu funkcji 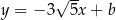 . Parametr
. Parametr 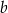 jest równy
jest równy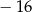
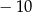
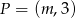 należy do wykresu funkcji liniowej
należy do wykresu funkcji liniowej 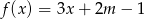 . Liczba
. Liczba 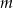 jest równa
jest równa 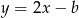 należy punkt
należy punkt 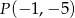 . Współczynnik
. Współczynnik 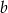 jest równy:
jest równy: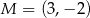 należy do wykresu funkcji liniowej
należy do wykresu funkcji liniowej 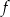 określonej wzorem
określonej wzorem 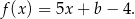
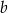 jest równe
jest równe 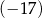
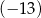
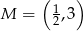 należy do wykresu funkcji liniowej określonej wzorem
należy do wykresu funkcji liniowej określonej wzorem 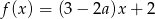 . Wtedy
. Wtedy 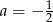
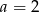
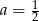
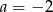
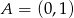 leży na wykresie funkcji liniowej
leży na wykresie funkcji liniowej 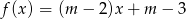 . Stąd wynika, że
. Stąd wynika, że 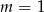
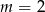
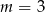
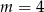
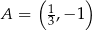 należy do wykresu funkcji liniowej
należy do wykresu funkcji liniowej 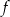 określonej wzorem
określonej wzorem 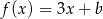 . Wynika stąd, że
. Wynika stąd, że 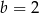
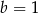
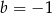
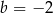
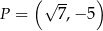 należy do wykresu funkcji
należy do wykresu funkcji 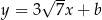 . Parametr
. Parametr 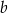 jest równy
jest równy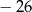
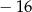
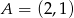 leży na wykresie funkcji liniowej
leży na wykresie funkcji liniowej 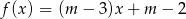 . Stąd wynika, że
. Stąd wynika, że 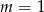
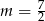
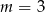
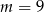
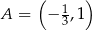 należy do wykresu funkcji liniowej
należy do wykresu funkcji liniowej 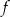 określonej wzorem
określonej wzorem 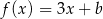 . Wynika stąd, że
. Wynika stąd, że 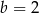
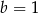
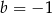
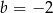
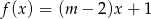 leży punkt
leży punkt 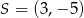 . Zatem
. Zatem 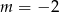
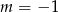
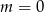
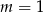
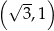 należy do wykresu funkcji
należy do wykresu funkcji 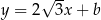 . Wtedy współczynnik
. Wtedy współczynnik 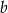 jest równy
jest równy 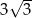
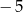
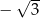
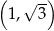 należy do wykresu funkcji
należy do wykresu funkcji 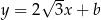 . Wtedy współczynnik
. Wtedy współczynnik 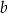 jest równy
jest równy 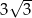
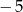
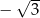
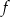 określona wzorem
określona wzorem 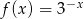 . Wykres funkcji
. Wykres funkcji 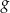 jest symetryczny do wykresu funkcji
jest symetryczny do wykresu funkcji 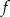 względem osi
względem osi 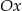 . Zatem
. Zatem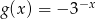
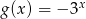
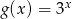
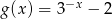
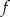 określona wzorem
określona wzorem 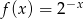 . Wykres funkcji
. Wykres funkcji 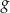 jest symetryczny do wykresu funkcji
jest symetryczny do wykresu funkcji 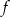 względem osi
względem osi 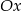 . Zatem
. Zatem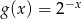
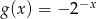
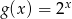
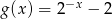
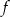 określona wzorem
określona wzorem 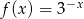 . Wykres funkcji
. Wykres funkcji 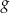 jest symetryczny do wykresu funkcji
jest symetryczny do wykresu funkcji 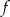 względem osi
względem osi 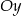 . Zatem
. Zatem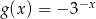
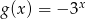
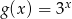
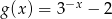
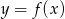 .
. 
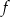 w przedziale
w przedziale 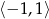 jest równa
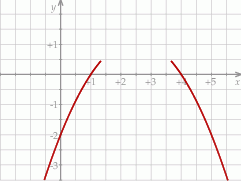
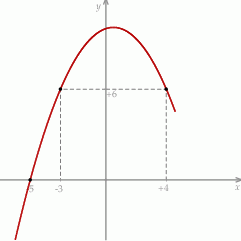
jest równa 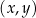 narysowano wykres funkcji
narysowano wykres funkcji 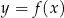 (zobacz rysunek).
(zobacz rysunek). 
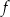 w przedziale
w przedziale ![[− 6,1 ]](https://img.zadania.info/zad/2225331/HzadT4x.png) jest równa
jest równa 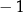
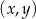 narysowano wykres funkcji
narysowano wykres funkcji 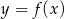 (zobacz rysunek).
(zobacz rysunek). 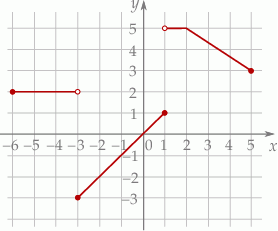
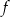 w przedziale
w przedziale ![[− 4,1 ]](https://img.zadania.info/zad/7035487/HzadT4x.gif) jest równa
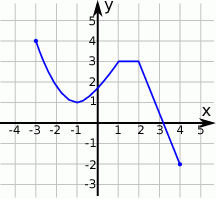
jest równa 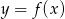 .
. 
 w przedziale
w przedziale 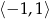 jest równa
jest równa 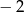
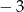
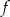 , wskaż nierówność prawdziwą
, wskaż nierówność prawdziwą 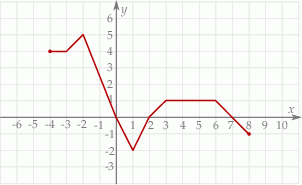
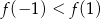
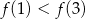
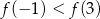
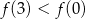
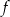 , wskaż nierówność prawdziwą
, wskaż nierówność prawdziwą 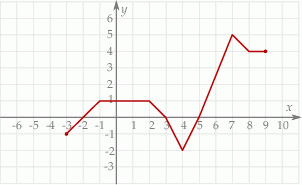
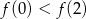
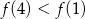
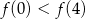
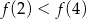
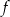 , wskaż nierówność prawdziwą
, wskaż nierówność prawdziwą 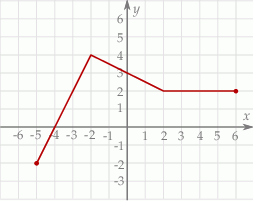
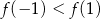
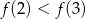
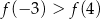
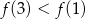
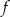 , wskaż nierówność prawdziwą
, wskaż nierówność prawdziwą 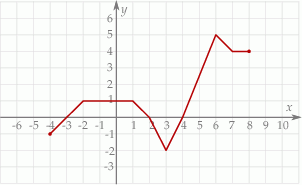
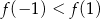
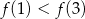
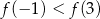
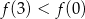
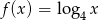 nie należy punkt
nie należy punkt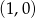
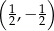
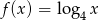 nie należy punkt
nie należy punkt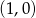
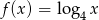 nie należy punkt
nie należy punkt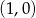
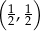
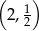
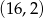
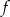 . Dziedziną funkcji
. Dziedziną funkcji 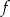 jest przedział
jest przedział 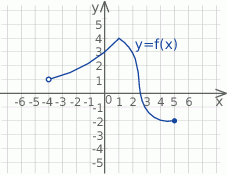
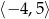
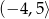
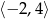
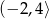
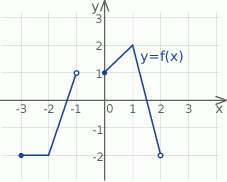
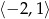
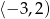
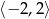
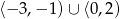
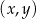 narysowano wykres funkcji
narysowano wykres funkcji 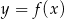 (zobacz rysunek).
(zobacz rysunek). 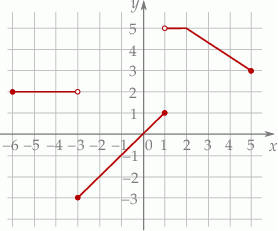
 jest zbiór
jest zbiór ![[− 6,5]](https://img.zadania.info/zad/6322164/HzadT4x.gif)
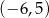
![(− 3,5]](https://img.zadania.info/zad/6322164/HzadT6x.gif)
![[− 3,5]](https://img.zadania.info/zad/6322164/HzadT7x.gif)
 .
. 
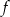 jest przedział
jest przedział 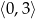
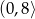
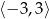
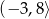
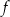 .
. 
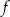 jest zbiór
jest zbiór 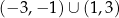
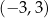
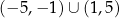
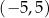
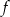 . Dziedziną funkcji
. Dziedziną funkcji 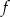 jest przedział
jest przedział 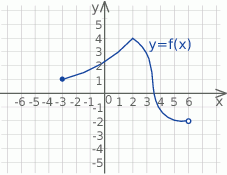
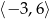
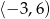
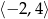
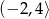
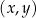 narysowano wykres funkcji
narysowano wykres funkcji 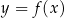 (zobacz rysunek).
(zobacz rysunek). 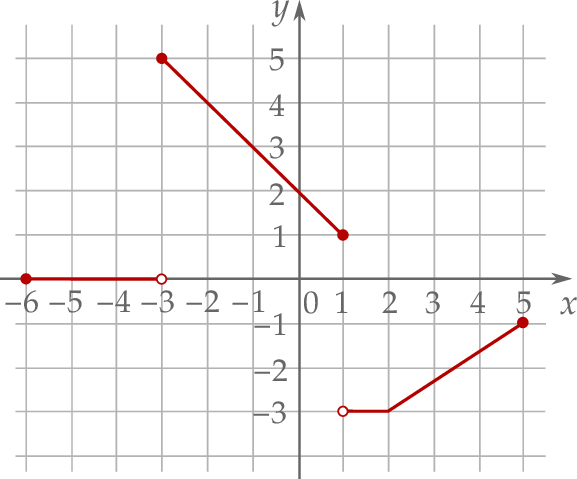
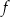 jest zbiór
jest zbiór 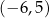
![[− 6,5]](https://img.zadania.info/zad/9554435/HzadT5x.png)
![(− 3,5]](https://img.zadania.info/zad/9554435/HzadT6x.png)
![[− 3,5]](https://img.zadania.info/zad/9554435/HzadT7x.png)
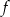 . Dziedziną funkcji
. Dziedziną funkcji 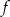 jest przedział
jest przedział 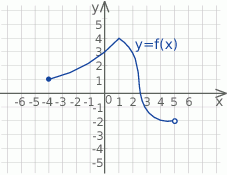
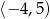
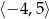
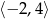
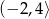
 jest funkcją kwadratową, dla której
jest funkcją kwadratową, dla której 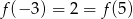 . Osią symetrii paraboli będącej wykresem tej funkcji jest prosta
. Osią symetrii paraboli będącej wykresem tej funkcji jest prosta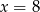
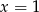
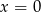
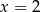
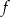 jest funkcją kwadratową, dla której
jest funkcją kwadratową, dla której 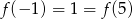 . Osią symetrii paraboli będącej wykresem tej funkcji jest prosta
. Osią symetrii paraboli będącej wykresem tej funkcji jest prosta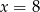
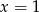
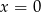
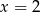
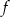 jest funkcją kwadratową, dla której
jest funkcją kwadratową, dla której 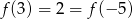 . Osią symetrii paraboli będącej wykresem tej funkcji jest prosta
. Osią symetrii paraboli będącej wykresem tej funkcji jest prosta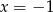
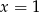
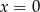
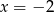
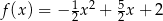
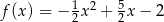
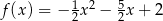
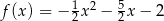
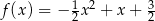
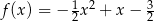
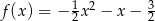
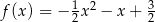
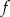 i
i 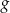 są określone dla wszystkich liczb rzeczywistych
są określone dla wszystkich liczb rzeczywistych 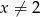 wzorami:
wzorami: 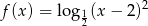 ,
, 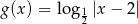 . Ile punktów wspólnych mają wykresy tych funkcji?
. Ile punktów wspólnych mają wykresy tych funkcji?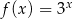 oraz
oraz 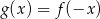 , określone dla wszystkich liczb rzeczywistych
, określone dla wszystkich liczb rzeczywistych  . Punkt wspólny wykresów funkcji
. Punkt wspólny wykresów funkcji 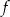 i
i 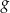
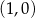
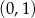
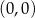
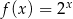 oraz
oraz 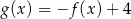 , określone dla wszystkich liczb rzeczywistych
, określone dla wszystkich liczb rzeczywistych  . Punkt wspólny wykresów funkcji
. Punkt wspólny wykresów funkcji 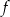 i
i 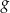
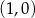
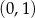
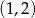
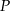 jest punktem wspólnym wykresu funkcji
jest punktem wspólnym wykresu funkcji 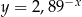 i prostej
i prostej 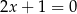 . Odległość punktu
. Odległość punktu 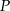 od osi
od osi 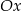 układu współrzędnych jest równa
układu współrzędnych jest równa 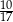
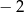
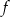 .
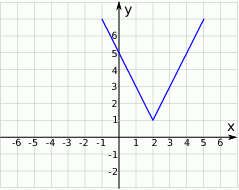
. 
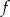 względem osi
względem osi 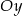 układu współrzędnych.
układu współrzędnych.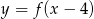
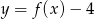
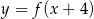
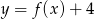
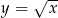 o dwie jednostki w górę otrzymujemy funkcję:
o dwie jednostki w górę otrzymujemy funkcję: 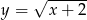
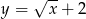
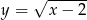
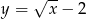
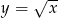 o dwie jednostki w dół otrzymujemy funkcję:
o dwie jednostki w dół otrzymujemy funkcję: 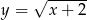
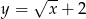
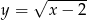
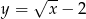
 jest określona wzorem
jest określona wzorem 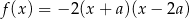 . Wierzchołek paraboli, która jest wykresem funkcji
. Wierzchołek paraboli, która jest wykresem funkcji 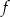 , ma współrzędną
, ma współrzędną 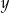 równą 2. Zatem liczba
równą 2. Zatem liczba  może być równa
może być równa 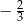

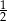
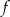 określonej w zbiorze
określonej w zbiorze 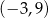 .
. 
 jest przedział
jest przedział 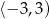
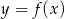 i
i 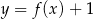 mają tyle samo miejsc zerowych
mają tyle samo miejsc zerowych 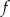 osiąga wartość równą 2 w trzech punktach.
osiąga wartość równą 2 w trzech punktach. 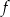 dla argumentu
dla argumentu 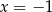 jest liczbą dodatnią.
jest liczbą dodatnią. 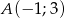 należy do wykresu funkcji:
należy do wykresu funkcji: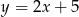
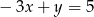
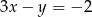
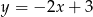
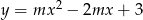 przechodzi przez punkty
przechodzi przez punkty 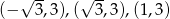 . Wtedy
. Wtedy 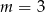
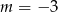
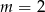
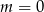
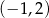 należy do wykresu funkcji
należy do wykresu funkcji 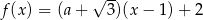 . Wynika stąd, że
. Wynika stąd, że 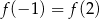
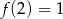
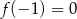
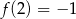
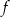 , określonej dla wszystkich liczb rzeczywistych. Do tego wykresu należą punkty
, określonej dla wszystkich liczb rzeczywistych. Do tego wykresu należą punkty 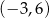 i
i 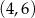 , a liczba
, a liczba 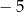 jest miejscem zerowym funkcji
jest miejscem zerowym funkcji 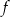 .
. 
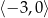 , to
, to