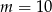Dana jest funkcja kwadratowa 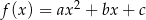 , gdzie
, gdzie 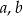 i
i  są liczbami rzeczywistymi takimi, że
są liczbami rzeczywistymi takimi, że 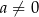 oraz
oraz 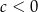 . Funkcja
. Funkcja 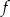 nie ma miejsc zerowych. Wykres funkcji
nie ma miejsc zerowych. Wykres funkcji 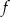 leży w całości
leży w całości
A) nad osią 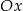 , , | B) pod osią 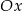 , , |
| ponieważ | |
| 1) | 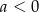 i i 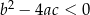 . . |
| 2) | 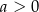 i i 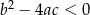 . . |
| 3) | 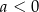 i i 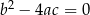 . . |
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Dana jest funkcja kwadratowa 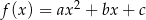 , gdzie
, gdzie 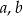 i
i  są liczbami rzeczywistymi takimi, że
są liczbami rzeczywistymi takimi, że 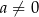 oraz
oraz 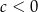 . Funkcja
. Funkcja 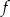 nie ma miejsc zerowych. Wykres funkcji
nie ma miejsc zerowych. Wykres funkcji 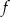 leży w całości
leży w całości
A) nad osią 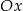 , , | B) pod osią 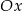 , , |
| ponieważ | |
| 1) | 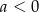 i i 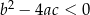 . . |
| 2) | 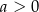 i i 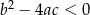 . . |
| 3) | 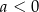 i i 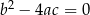 . . |
Dana jest funkcja kwadratowa 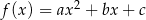 , gdzie
, gdzie 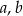 i
i  są liczbami rzeczywistymi takimi, że
są liczbami rzeczywistymi takimi, że 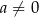 oraz
oraz 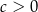 . Funkcja
. Funkcja 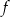 nie ma miejsc zerowych. Wykres funkcji
nie ma miejsc zerowych. Wykres funkcji 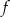 leży w całości
leży w całości
A) nad osią 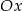 , , | B) pod osią 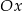 , , |
| ponieważ | |
| 1) | 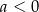 i i 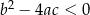 . . |
| 2) | 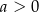 i i 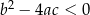 . . |
| 3) | 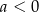 i i 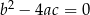 . . |
W kartezjańskim układzie współrzędnych  narysowano wykres funkcji
narysowano wykres funkcji 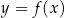 (zobacz rysunek).
(zobacz rysunek).
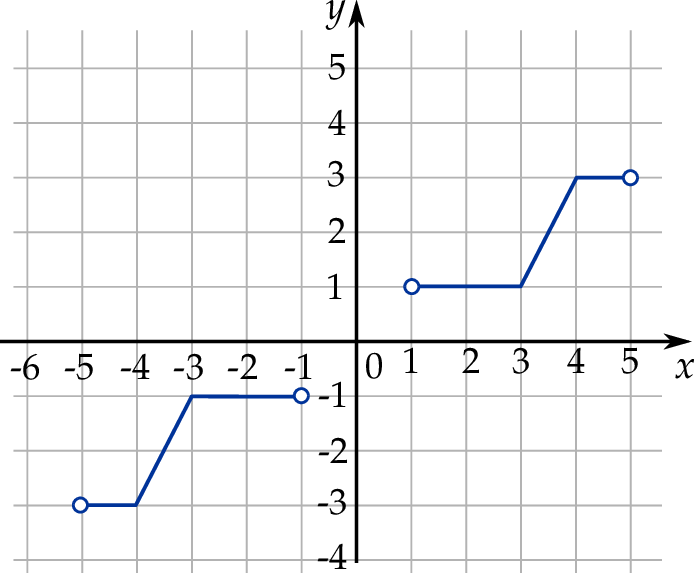
Zbiorem wartości funkcji 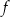 jest zbiór
jest zbiór
A) ![[− 3,− 1]∪ [1,3]](https://img.zadania.info/zad/7474248/HzadT4x.png) B)
B) 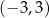 C)
C) 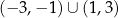
D) ![[− 5,− 1]∪ [1,5]](https://img.zadania.info/zad/7474248/HzadT7x.png) E)
E) 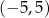 F)
F) 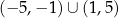
W kartezjańskim układzie współrzędnych  narysowano wykres funkcji
narysowano wykres funkcji 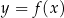 (zobacz rysunek).
(zobacz rysunek).
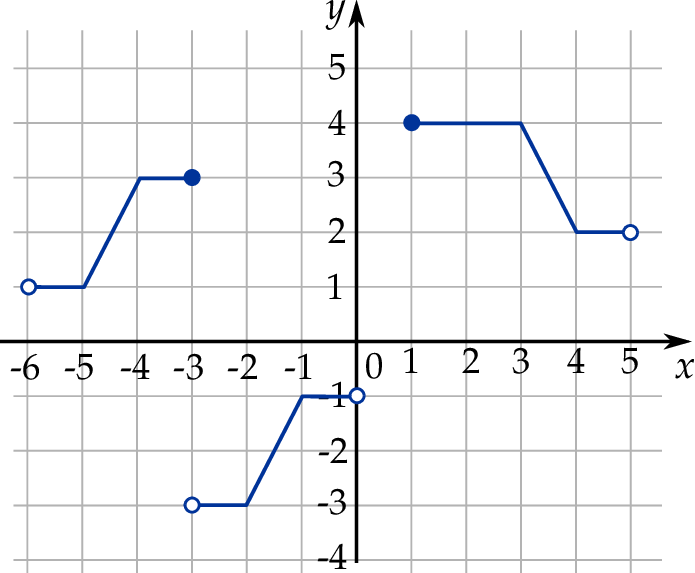
Zbiorem wartości funkcji  jest zbiór
jest zbiór
A)  B)
B) ![[− 3,4]](https://img.zadania.info/zad/5016823/HzadT5x.png) C)
C) 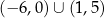
D) ![[− 3,− 1)∪ (1 ,4 ]](https://img.zadania.info/zad/5016823/HzadT7x.png) E)
E) ![(− 3,4 ]](https://img.zadania.info/zad/5016823/HzadT8x.png) F)
F) ![[− 3,− 1] ∪ [1 ,4 ]](https://img.zadania.info/zad/5016823/HzadT9x.png)
Dana jest funkcja kwadratowa 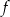 , której fragment wykresu przedstawiono w kartezjańskim układzie współrzędnych
, której fragment wykresu przedstawiono w kartezjańskim układzie współrzędnych 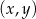 na rysunku poniżej. Wierzchołek paraboli, która jest wykresem funkcji
na rysunku poniżej. Wierzchołek paraboli, która jest wykresem funkcji 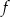 , oraz punkty przecięcia paraboli z osiami układu współrzędnych mają współrzędne całkowite.
, oraz punkty przecięcia paraboli z osiami układu współrzędnych mają współrzędne całkowite.
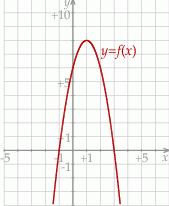
Funkcja 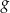 jest określona za pomocą funkcji
jest określona za pomocą funkcji 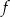 następująco:
następująco: 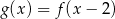 . Wykres funkcji
. Wykres funkcji 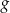 przedstawiono na rysunku
przedstawiono na rysunku
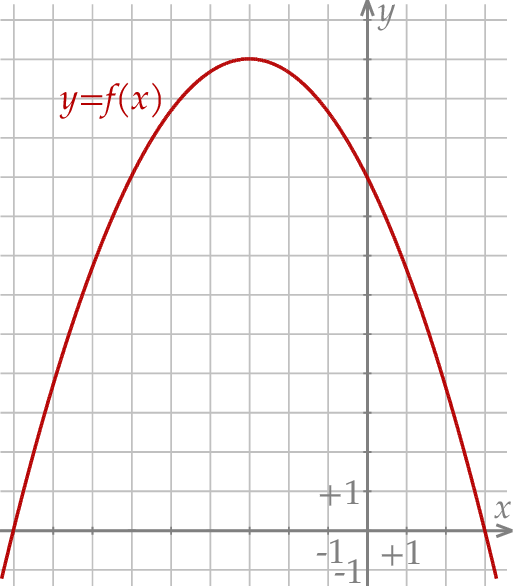
W kartezjańskim układzie współrzędnych  przedstawiono fragment wykresu funkcji kwadratowej
przedstawiono fragment wykresu funkcji kwadratowej  (zobacz rysunek). Wierzchołek paraboli, która jest wykresem funkcji
(zobacz rysunek). Wierzchołek paraboli, która jest wykresem funkcji 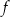 , oraz punkty przecięcia paraboli z osiami układu współrzędnych mają współrzędne całkowite.
, oraz punkty przecięcia paraboli z osiami układu współrzędnych mają współrzędne całkowite.
Funkcja kwadratowa 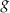 jest określona za pomocą funkcji
jest określona za pomocą funkcji 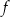 następująco:
następująco: 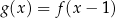 . Fragment wykresu funkcji
. Fragment wykresu funkcji 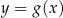 przedstawiono na rysunku
przedstawiono na rysunku
W kartezjańskim układzie współrzędnych 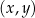 przedstawiono fragment wykresu funkcji kwadratowej
przedstawiono fragment wykresu funkcji kwadratowej 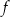 (zobacz rysunek). Wierzchołek paraboli, która jest wykresem funkcji
(zobacz rysunek). Wierzchołek paraboli, która jest wykresem funkcji 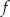 , oraz punkty przecięcia paraboli z osiami układu współrzędnych mają współrzędne całkowite.
, oraz punkty przecięcia paraboli z osiami układu współrzędnych mają współrzędne całkowite.
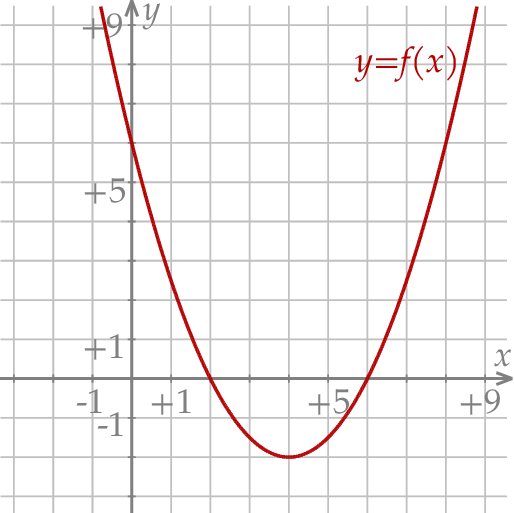
Funkcja kwadratowa 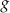 jest określona za pomocą funkcji
jest określona za pomocą funkcji 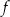 następująco:
następująco: 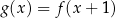 . Fragment wykresu funkcji
. Fragment wykresu funkcji 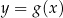 przedstawiono na rysunku
przedstawiono na rysunku
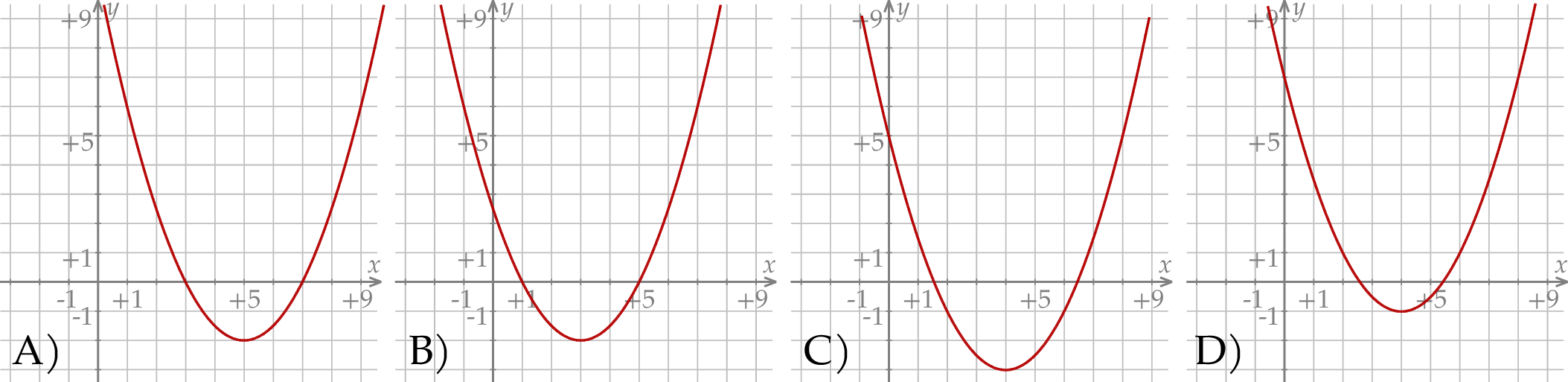
Dana jest funkcja kwadratowa 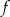 , której fragment wykresu przedstawiono na rysunku poniżej. Wierzchołek paraboli, która jest wykresem funkcji
, której fragment wykresu przedstawiono na rysunku poniżej. Wierzchołek paraboli, która jest wykresem funkcji 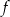 , oraz punkty przecięcia paraboli z osiami układu współrzędnych mają współrzędne całkowite.
, oraz punkty przecięcia paraboli z osiami układu współrzędnych mają współrzędne całkowite.
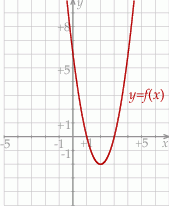
Funkcja 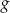 jest określona za pomocą funkcji
jest określona za pomocą funkcji 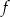 następująco:
następująco: 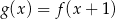 . Wykres funkcji
. Wykres funkcji 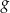 przedstawiono na rysunku
przedstawiono na rysunku
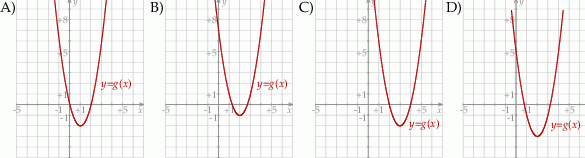
Parabola o wierzchołku 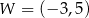 i ramionach skierowanych w dół może być wykresem funkcji określonej wzorem
i ramionach skierowanych w dół może być wykresem funkcji określonej wzorem
A) 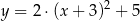 B)
B) 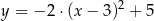
C) 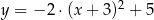 D)
D) 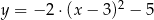
Punkt 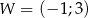 jest wierzchołkiem wykresu funkcji kwadratowej
jest wierzchołkiem wykresu funkcji kwadratowej 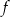 . Wobec tego funkcję
. Wobec tego funkcję 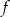 może przedstawiać wzór
może przedstawiać wzór
A) 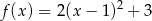 B)
B) 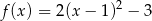
C) 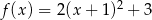 D)
D) 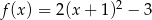
Parabola o wierzchołku 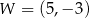 i ramionach skierowanych w dół może być wykresem funkcji określonej wzorem
i ramionach skierowanych w dół może być wykresem funkcji określonej wzorem
A) 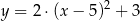 B)
B) 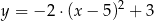
C) 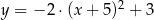 D)
D) 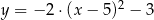
Na rysunku poniżej przedstawiony jest fragment wykresu funkcji liniowej 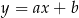 .
.
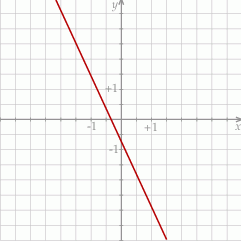
Jakie nierówności spełniają współczynniki  i
i 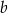 ?
?
A) 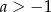 i
i 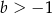 B)
B) 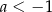 i
i 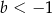 C)
C) 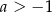 i
i 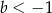 D)
D)  i
i 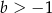
Na rysunku przedstawiono fragment wykresu funkcji liniowej 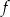 określonej wzorem
określonej wzorem 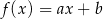 .
.
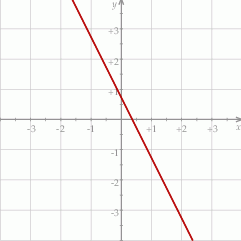
Współczynniki  oraz
oraz 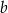 we wzorze funkcji
we wzorze funkcji 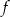 spełniają zależność
spełniają zależność
A) 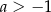 i
i 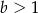 B)
B) 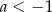 i
i 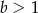 C)
C) 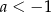 i
i 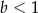 D)
D) 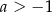 i
i 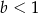
Wierzchołek paraboli opisanej wzorem 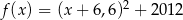 należy do
należy do
A) I ćwiartki układu współrzędnych B) II ćwiartki układu współrzędnych
C) III ćwiartki układu współrzędnych D) IV ćwiartki układu współrzędnych
Na rysunku przedstawiono fragment wykresu pochodnej 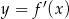 funkcji
funkcji 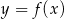 .
.
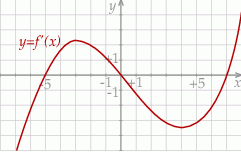
Wynika stąd, że
A) 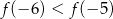 B)
B) 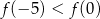 C)
C) 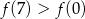 D)
D) 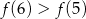
Na rysunku przedstawiono fragment wykresu pochodnej 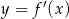 funkcji
funkcji 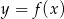 .
.
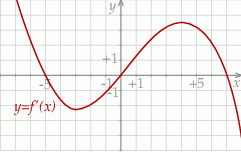
Wynika stąd, że
A) 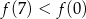 B)
B) 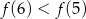 C)
C) 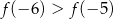 D)
D) 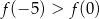
Funkcja  określona jest wzorem
określona jest wzorem 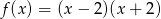 . Funkcja
. Funkcja 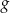 określona jest wzorem
określona jest wzorem 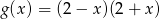 . Wykres funkcji
. Wykres funkcji 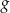 można otrzymać z wykresu funkcji
można otrzymać z wykresu funkcji 
A) przesuwając go o 2 jednostki w dół wzdłuż osi 
B) przesuwając go o 2 jednostki w lewo wzdłuż osi 
C) w symetrii względem osi 
D) w symetrii względem osi 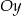
Funkcja 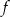 określona jest wzorem
określona jest wzorem 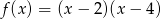 . Funkcja
. Funkcja 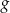 określona jest wzorem
określona jest wzorem 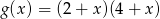 . Wykres funkcji
. Wykres funkcji 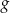 można otrzymać z wykresu funkcji
można otrzymać z wykresu funkcji 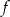
A) przesuwając go o 3 jednostki w dół wzdłuż osi 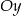
B) przesuwając go o 3 jednostki w lewo wzdłuż osi 
C) w symetrii względem osi 
D) w symetrii względem osi 
Funkcja 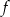 określona jest wzorem
określona jest wzorem 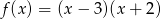 . Funkcja
. Funkcja 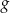 określona jest wzorem
określona jest wzorem 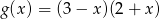 . Wykres funkcji
. Wykres funkcji 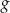 można otrzymać z wykresu funkcji
można otrzymać z wykresu funkcji 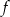
A) w symetrii względem osi 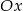
B) przesuwając go o 2 jednostki w lewo wzdłuż osi 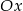
C) przesuwając go o 4 jednostki w dół wzdłuż osi 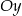
D) w symetrii względem osi 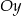
Na rysunku obok jest przedstawiony fragment wykresu funkcji kwadratowej 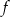 . Osią symetrii paraboli jest prosta o równaniu
. Osią symetrii paraboli jest prosta o równaniu 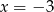 .
.
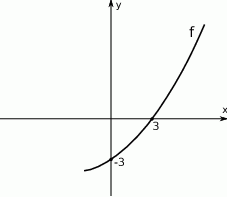
Rozwiązaniem nierówności 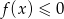 jest zbiór
jest zbiór
A) 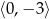 B)
B) 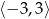 C)
C) 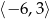 D)
D) 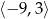
Dana jest parabola o równaniu 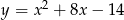 . Pierwsza współrzędna wierzchołka tej paraboli jest równa
. Pierwsza współrzędna wierzchołka tej paraboli jest równa
A) 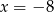 B)
B) 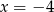 C)
C) 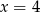 D)
D) 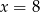
Dana jest parabola o równaniu 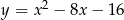 . Pierwsza współrzędna wierzchołka tej paraboli jest równa
. Pierwsza współrzędna wierzchołka tej paraboli jest równa
A) 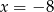 B)
B) 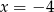 C)
C) 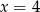 D)
D) 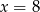
Wykres funkcji liniowej 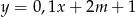 przecina dodatnią półoś
przecina dodatnią półoś  wtedy i tylko wtedy, gdy
wtedy i tylko wtedy, gdy
A) 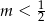 B)
B) 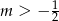 C)
C) 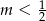 D)
D) 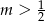
Wykres funkcji liniowej 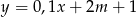 przechodzi przez początek układu współrzędnych wtedy i tylko wtedy, gdy
przechodzi przez początek układu współrzędnych wtedy i tylko wtedy, gdy
A) 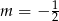 B)
B) 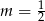 C)
C) 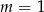 D)
D) 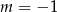
Wykres funkcji liniowej 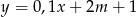 przecina ujemną półoś
przecina ujemną półoś 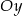 wtedy i tylko wtedy, gdy
wtedy i tylko wtedy, gdy
A) 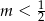 B)
B) 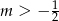 C)
C) 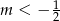 D)
D) 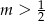
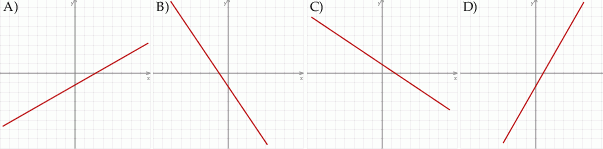
Na którym rysunku przedstawiono wykres funkcji liniowej 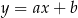 takiej, że
takiej, że  ?
?
Na którym rysunku przedstawiono wykres funkcji liniowej  takiej, że
takiej, że 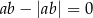 ?
?
Na rysunku 1 jest przedstawiony wykres funkcji 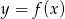 .
.
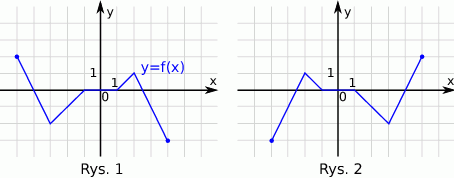
Funkcja przedstawiona na rysunku 2 jest określona wzorem
A) 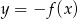 B)
B) 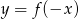 C)
C) 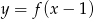 D)
D) 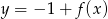
Na rysunku 1. jest przedstawiony wykres funkcji 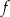 , a na rysunku 2. – wykres funkcji
, a na rysunku 2. – wykres funkcji 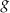 .
.
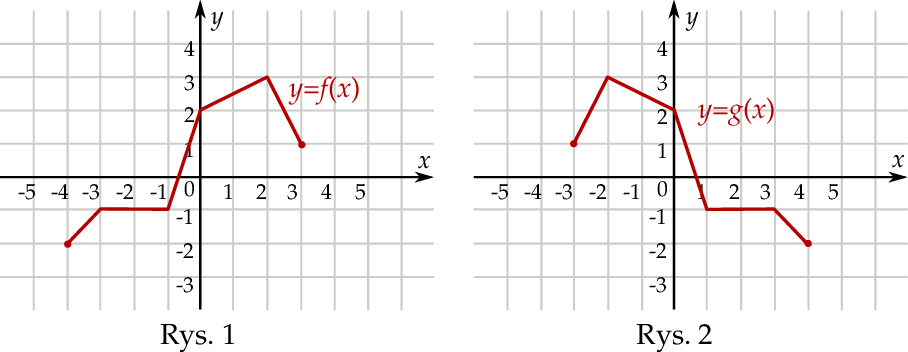
Funkcja  jest określona wzorem
jest określona wzorem
A) 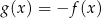 B)
B) 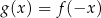 C)
C) 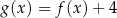 D)
D) 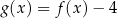
Na rysunku 1. jest przedstawiony wykres funkcji 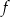 , a na rysunku 2. – wykres funkcji
, a na rysunku 2. – wykres funkcji 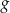 .
.
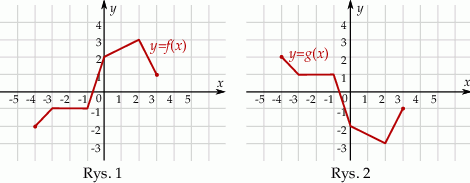
Funkcja 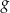 jest określona wzorem
jest określona wzorem
A) 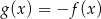 B)
B) 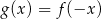 C)
C) 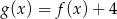 D)
D) 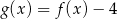
Na rysunku 1 jest przedstawiony wykres funkcji 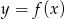 .
.
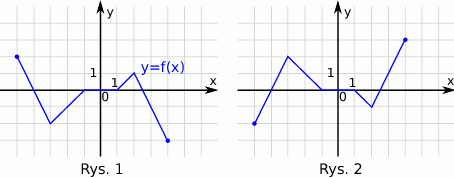
Funkcja przedstawiona na rysunku 2 jest określona wzorem
A) 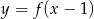 B)
B) 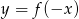 C)
C) 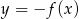 D)
D) 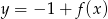
Liczba punktów wspólnych wykresów funkcji 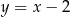 i
i 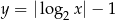 jest równa
jest równa
A) 0 B) 1 C) 2 D) 3
Na rysunku przedstawiony jest fragment wykresu pewnej funkcji liniowej 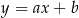 .
.
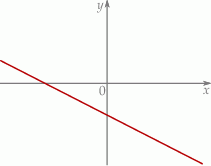
Jakie znaki mają współczynniki  i
i 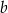 ?
?
A) 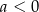 i
i 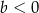 B)
B) 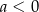 i
i 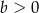 C)
C) 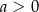 i
i 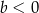 D)
D) 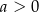 i
i 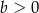
Na rysunku przedstawiono fragment wykresu funkcji liniowej 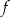 określonej wzorem
określonej wzorem 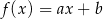 .
.
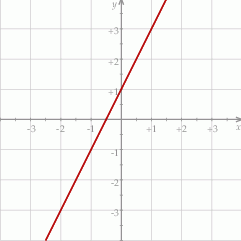
Współczynniki  oraz
oraz 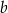 we wzorze funkcji
we wzorze funkcji 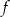 spełniają zależność
spełniają zależność
A) 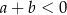 B)
B) 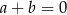 C)
C) 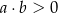 D)
D) 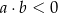
Na rysunku przedstawiono fragment wykresu funkcji liniowej 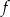 określonej wzorem
określonej wzorem 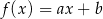 .
.
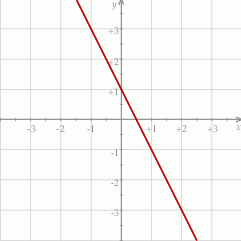
Współczynniki  oraz
oraz 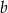 we wzorze funkcji
we wzorze funkcji 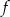 spełniają zależność
spełniają zależność
A) 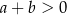 B)
B) 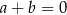 C)
C) 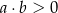 D)
D) 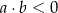
Dana jest funkcja liniowa 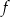 określona wzorem
określona wzorem 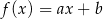 , gdzie
, gdzie  i
i 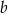 są liczbami rzeczywistymi. Wykres funkcji
są liczbami rzeczywistymi. Wykres funkcji 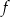 przedstawiono w kartezjańskim układzie współrzędnych
przedstawiono w kartezjańskim układzie współrzędnych 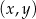 na rysunku poniżej
na rysunku poniżej
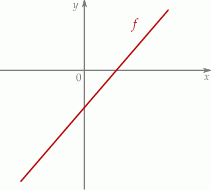
Współczynniki  i
i 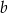 we wzorze funkcji
we wzorze funkcji 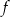 spełniają warunki
spełniają warunki
A) 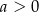 i
i 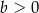 B)
B) 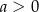 i
i 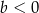 C)
C) 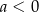 i
i 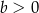 D)
D) 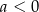 i
i 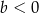
Funkcja liniowa 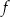 jest określona wzorem
jest określona wzorem 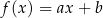 , gdzie
, gdzie  i
i 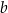 są pewnymi liczbami rzeczywistymi. Na rysunku obok przedstawiono fragment wykresu funkcji
są pewnymi liczbami rzeczywistymi. Na rysunku obok przedstawiono fragment wykresu funkcji 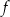 w kartezjańskim układzie współrzędnych
w kartezjańskim układzie współrzędnych 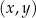 .
.
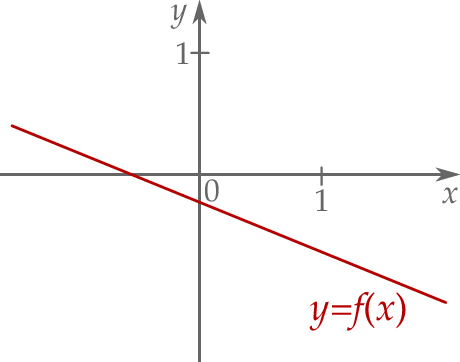
Liczba  oraz liczba
oraz liczba 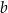 we wzorze funkcji
we wzorze funkcji 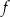 spełniają warunki:
spełniają warunki:
A) 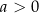 i
i 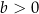 B)
B) 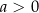 i
i 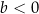 C)
C) 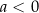 i
i 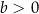 D)
D) 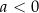 i
i 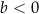
Na rysunku przedstawiono wykres funkcji liniowej 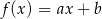 . Zatem
. Zatem
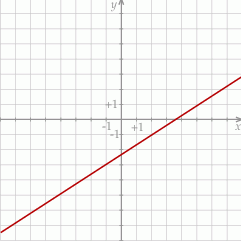
A) 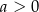 i
i 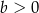 B)
B) 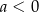 i
i 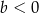 C)
C) 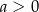 i
i 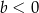 D)
D) 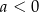 i
i 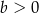
Dana jest funkcja liniowa 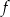 określona wzorem
określona wzorem 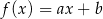 , gdzie
, gdzie  i
i 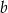 są liczbami rzeczywistymi. Wykres funkcji
są liczbami rzeczywistymi. Wykres funkcji 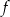 przedstawiono w kartezjańskim układzie współrzędnych
przedstawiono w kartezjańskim układzie współrzędnych 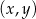 na rysunku poniżej
na rysunku poniżej
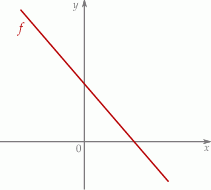
Współczynniki  i
i 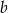 we wzorze funkcji
we wzorze funkcji 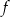 spełniają warunki
spełniają warunki
A) 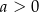 i
i 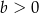 B)
B) 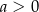 i
i 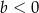 C)
C) 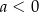 i
i 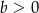 D)
D) 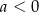 i
i 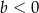
Na rysunku przedstawiony jest fragment wykresu pewnej funkcji liniowej 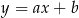 .
.
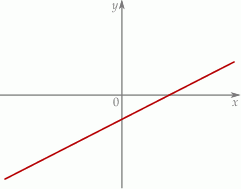
Jakie znaki mają współczynniki  i
i 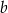 ?
?
A) 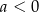 i
i 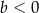 B)
B) 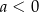 i
i 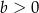 C)
C) 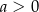 i
i 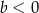 D)
D) 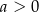 i
i 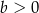
Funkcja liniowa 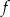 jest określona wzorem
jest określona wzorem 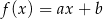 , gdzie
, gdzie  i
i 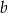 są pewnymi liczbami rzeczywistymi. Na rysunku obok przedstawiono fragment wykresu funkcji
są pewnymi liczbami rzeczywistymi. Na rysunku obok przedstawiono fragment wykresu funkcji 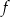 w kartezjańskim układzie współrzędnych
w kartezjańskim układzie współrzędnych 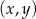 .
.
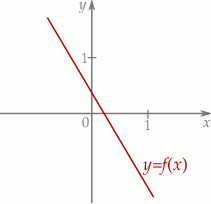
Liczba  oraz liczba
oraz liczba 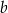 we wzorze funkcji
we wzorze funkcji 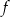 spełniają warunki:
spełniają warunki:
A) 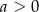 i
i 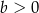 B)
B) 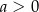 i
i 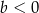 C)
C) 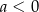 i
i 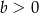 D)
D) 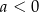 i
i 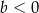
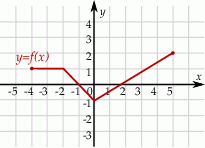
Korzystając z danego wykresu funkcji 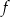 , wskaż nierówność prawdziwą
, wskaż nierówność prawdziwą
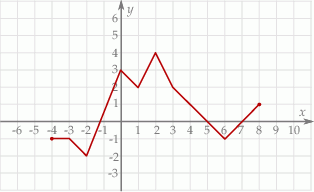
A) 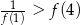 B)
B) ![[f (−3 )]2 < f (4)](https://img.zadania.info/zad/7980393/HzadT3x.gif) C)
C) 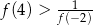 D)
D) ![2 f(3) > [f (3)]](https://img.zadania.info/zad/7980393/HzadT5x.gif)
Rysunek przedstawia wykres funkcji 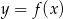 .
.
Wskaż rysunek, na którym przedstawiony jest wykres funkcji 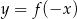 .
.
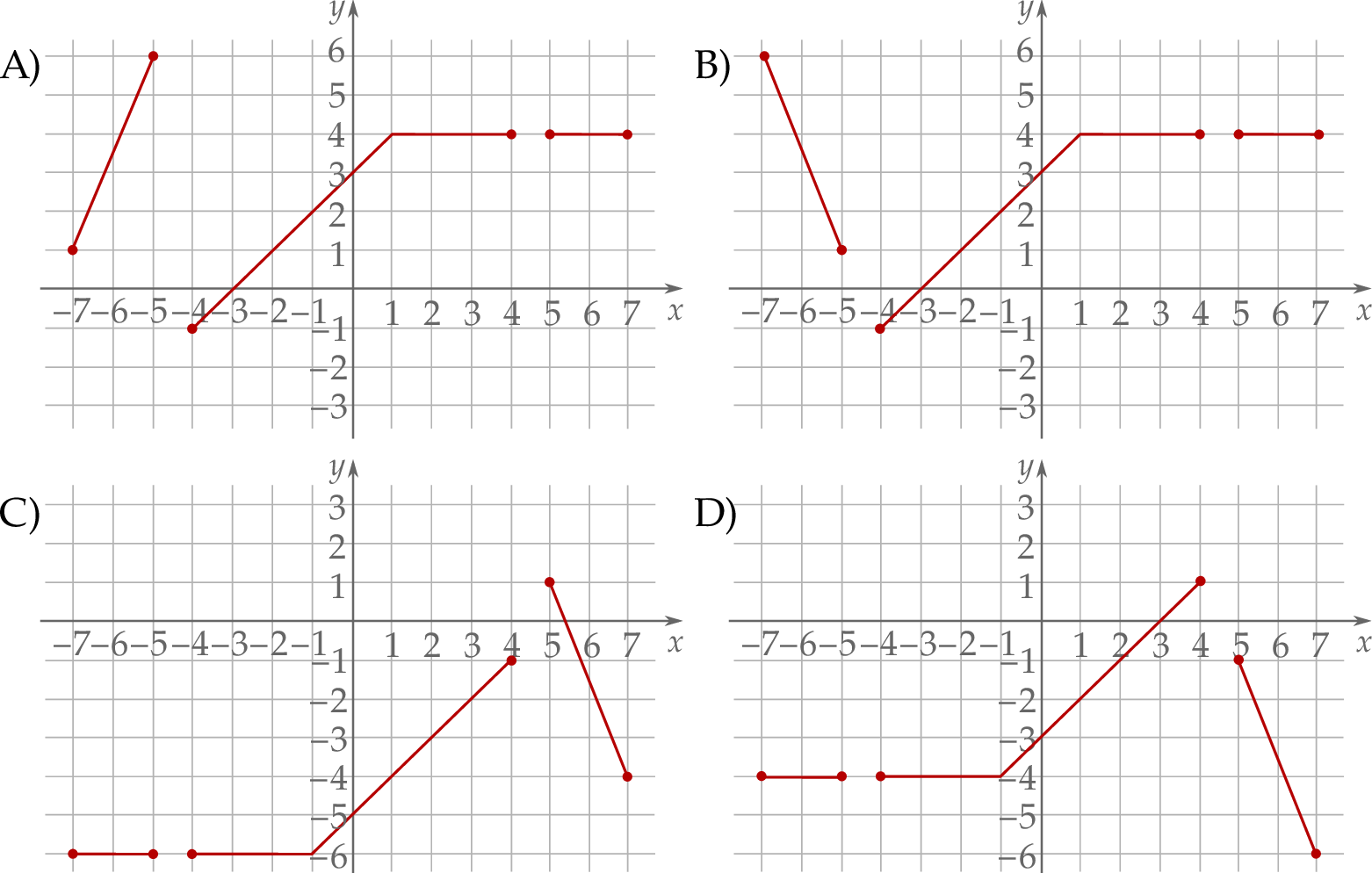
W kartezjańskim układzie współrzędnych  narysowano wykres funkcji
narysowano wykres funkcji  (zobacz rysunek).
(zobacz rysunek).
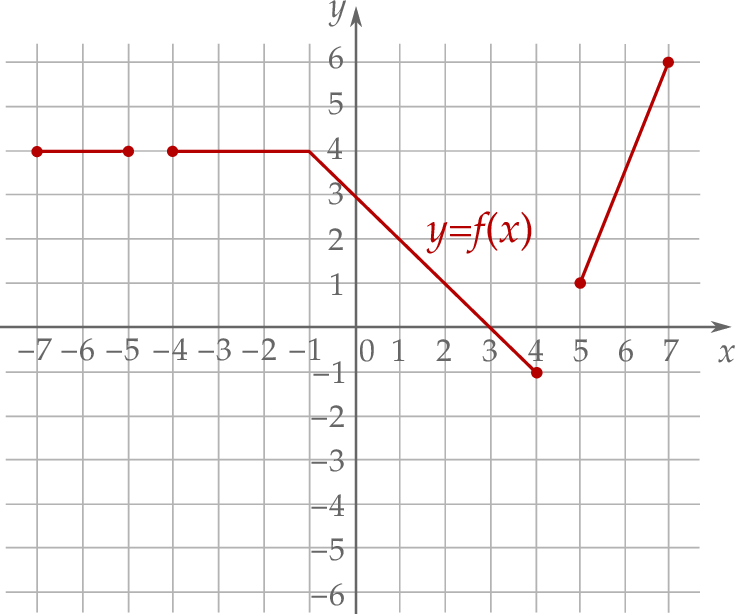
Funkcja 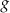 jest określona za pomocą funkcji
jest określona za pomocą funkcji 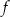 następująco:
następująco: 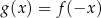 dla każdego
dla każdego ![x ∈ [− 7,− 5] ∪ [− 4,4 ]∪ [5 ,7]](https://img.zadania.info/zad/7097707/HzadT6x.png) . Na jednym z rysunków A–D przedstawiono, w kartezjańskim układzie współrzędnych
. Na jednym z rysunków A–D przedstawiono, w kartezjańskim układzie współrzędnych 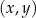 , wykres funkcji
, wykres funkcji 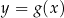 . Wykres funkcji
. Wykres funkcji 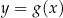 przedstawiono na rysunku
przedstawiono na rysunku
Rysunek przedstawia wykres funkcji 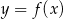 .
.
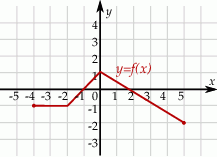
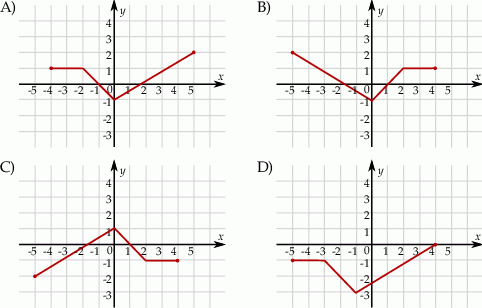
Wskaż rysunek, na którym przedstawiony jest wykres funkcji  .
.
Gdy przesuniemy wykres funkcji 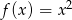 o 7 jednostek w lewo i 4 jednostki w dół, to otrzymamy wykres funkcji
o 7 jednostek w lewo i 4 jednostki w dół, to otrzymamy wykres funkcji
A) 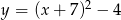 B)
B) 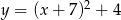 C)
C) 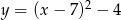 D)
D) 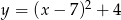
Wykres funkcji 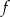 określonej wzorem
określonej wzorem 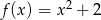 przesuwamy o 4 jednostki w dół wzdłuż osi
przesuwamy o 4 jednostki w dół wzdłuż osi 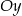 i o 2 jednostki w prawo wzdłuż osi
i o 2 jednostki w prawo wzdłuż osi 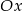 . Otrzymujemy w ten sposób wykres funkcji
. Otrzymujemy w ten sposób wykres funkcji 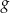 określonej wzorem
określonej wzorem
A) 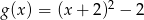
B) 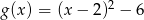
C) 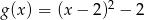
D) 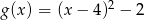
Wykresem funkcji kwadratowej 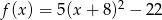 jest parabola, której oś symetrii ma równanie:
jest parabola, której oś symetrii ma równanie:
A) 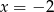 B)
B) 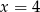 C)
C) 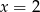 D)
D) 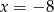
Prosta o równaniu 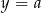 ma dokładnie jeden punkt wspólny z wykresem funkcji kwadratowej
ma dokładnie jeden punkt wspólny z wykresem funkcji kwadratowej 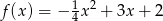 . Wynika stąd, że
. Wynika stąd, że
A) 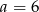 B)
B) 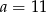 C)
C) 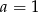 D)
D) 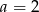
Prosta o równaniu 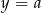 ma dokładnie jeden punkt wspólny z wykresem funkcji kwadratowej
ma dokładnie jeden punkt wspólny z wykresem funkcji kwadratowej 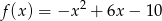 . Wynika stąd, że
. Wynika stąd, że
A) 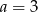 B)
B) 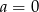 C)
C) 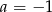 D)
D) 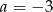
Prosta o równaniu 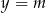 ma dokładnie jeden punkt wspólny z wykresem funkcji kwadratowej
ma dokładnie jeden punkt wspólny z wykresem funkcji kwadratowej 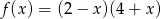 dla
dla
A) 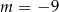 B)
B) 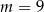 C)
C) 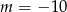 D)
D)