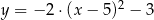Wierzchołek 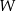 paraboli, będącej wykresem funkcji
paraboli, będącej wykresem funkcji 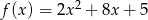 przesunięto o wektor
przesunięto o wektor 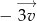 , gdzie
, gdzie ![→ v = [− 4;5]](https://img.zadania.info/zad/6882016/HzadT3x.gif) , otrzymując punkt
, otrzymując punkt 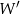 . Współrzędne punktu
. Współrzędne punktu 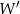 są równe
są równe
A) 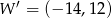 B)
B) 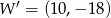 C)
C) 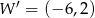 D)
D) 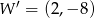
/Szkoła średnia/Zadania testowe/Funkcje - wykresy
Liczba 1 jest miejscem zerowym funkcji liniowej 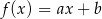 , a punkt
, a punkt 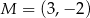 należy do wykresu tej funkcji. Współczynnik
należy do wykresu tej funkcji. Współczynnik  we wzorze tej funkcji jest równy
we wzorze tej funkcji jest równy
A) 1 B)  C)
C) 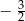 D)
D) 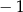
Liczba 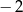 jest miejscem zerowym funkcji liniowej
jest miejscem zerowym funkcji liniowej 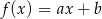 , a punkt
, a punkt 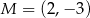 należy do wykresu tej funkcji. Współczynnik
należy do wykresu tej funkcji. Współczynnik  we wzorze tej funkcji jest równy
we wzorze tej funkcji jest równy
A) 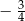 B)
B)  C)
C) 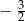 D)
D) 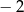
Wskaż wzór funkcji, która przecina osie układu współrzędnych w 3 punktach.
A) 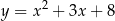 B)
B) 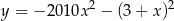
C) 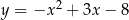 D)
D) 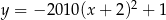
Wskaż wzór funkcji, która przecina osie układu współrzędnych w 3 punktach.
A) 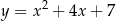 B)
B) 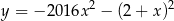
C) 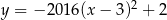 D)
D) 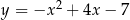
Funkcja liniowa 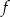 jest określona wzorem
jest określona wzorem 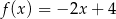 . Wykres funkcji
. Wykres funkcji 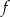 przesunięto wzdłuż osi
przesunięto wzdłuż osi 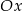 o 2 jednostki w lewo (tzn. przeciwnie do zwrotu osi), w wyniku czego otrzymano wykres funkcji
o 2 jednostki w lewo (tzn. przeciwnie do zwrotu osi), w wyniku czego otrzymano wykres funkcji 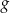 . Funkcja
. Funkcja 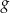 jest określona wzorem
jest określona wzorem
A) 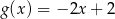 B)
B) 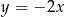 C)
C) 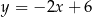 D)
D) 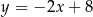
Funkcja liniowa 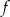 jest określona wzorem
jest określona wzorem 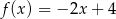 . Wykres funkcji
. Wykres funkcji 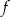 przesunięto wzdłuż osi
przesunięto wzdłuż osi 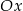 o 2 jednostki w prawo (tzn. zgodnie ze zwrotem osi), w wyniku czego otrzymano wykres funkcji
o 2 jednostki w prawo (tzn. zgodnie ze zwrotem osi), w wyniku czego otrzymano wykres funkcji 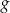 . Funkcja
. Funkcja 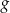 jest określona wzorem
jest określona wzorem
A) 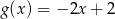 B)
B) 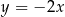 C)
C) 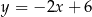 D)
D) 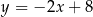
Funkcja kwadratowa 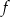 określona jest wzorem
określona jest wzorem 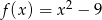 . Aby wykres tej funkcji miał dokładnie jeden punkt wspólny z prostą
. Aby wykres tej funkcji miał dokładnie jeden punkt wspólny z prostą 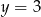 , należy go przesunąć o
, należy go przesunąć o
A) 12 jednostek w prawo wzdłuż osi 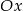
B) 12 jednostek do góry wzdłuż osi 
C) 12 jednostek do dołu wzdłuż osi 
D) 3 jednostki w lewo wzdłuż osi 
Funkcja kwadratowa 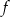 określona jest wzorem
określona jest wzorem 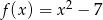 . Aby wykres tej funkcji miał dokładnie jeden punkt wspólny z prostą
. Aby wykres tej funkcji miał dokładnie jeden punkt wspólny z prostą 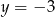 , należy go przesunąć o
, należy go przesunąć o
A) 4 jednostki do góry wzdłuż osi 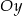
B) 10 jednostek do góry wzdłuż osi 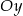
C) 4 jednostki w dół wzdłuż osi 
D) 10 jednostek w dół wzdłuż osi 
Funkcja kwadratowa 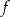 określona jest wzorem
określona jest wzorem 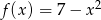 . Aby wykres tej funkcji miał dokładnie jeden punkt wspólny z prostą
. Aby wykres tej funkcji miał dokładnie jeden punkt wspólny z prostą 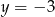 , należy go przesunąć o
, należy go przesunąć o
A) 4 jednostki do góry wzdłuż osi 
B) 10 jednostek do góry wzdłuż osi 
C) 4 jednostki w dół wzdłuż osi 
D) 10 jednostek w dół wzdłuż osi 
Dane są funkcje 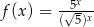 oraz
oraz 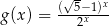 , określone dla wszystkich liczb rzeczywistych
, określone dla wszystkich liczb rzeczywistych  . Punkt wspólny wykresów funkcji
. Punkt wspólny wykresów funkcji 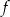 i
i 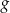
A) nie istnieje B) ma współrzędne 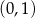
C) ma współrzędne 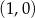 D) ma współrzędne
D) ma współrzędne 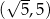
Na rysunku przedstawione są wykresy funkcji 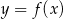 oraz
oraz 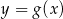 .
.
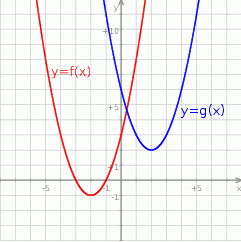
Wówczas :
A) 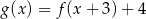 B)
B) 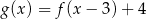
C) 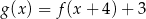 D)
D) 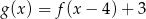
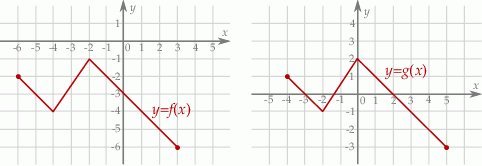
Na rysunkach przedstawione są wykresy funkcji 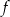 i
i 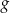 .
.
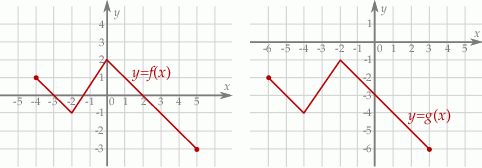
Wykres funkcji 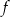 przekształcono i otrzymano wykres funkcji
przekształcono i otrzymano wykres funkcji 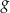 , zatem
, zatem
A) 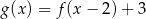 B)
B) 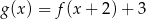
C) 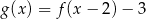 D)
D) 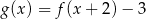
Na rysunkach przedstawione są wykresy funkcji 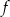 i
i 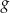 .
.
Wykres funkcji 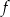 przekształcono i otrzymano wykres funkcji
przekształcono i otrzymano wykres funkcji 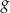 , zatem
, zatem
A) 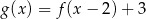 B)
B) 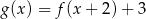
C) 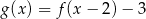 D)
D) 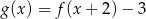
Na rysunku przedstawione są wykresy funkcji 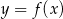 oraz
oraz 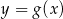 .
.
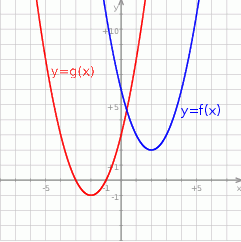
Wówczas :
A) 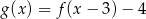 B)
B) 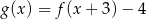
C) 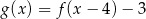 D)
D) 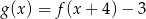
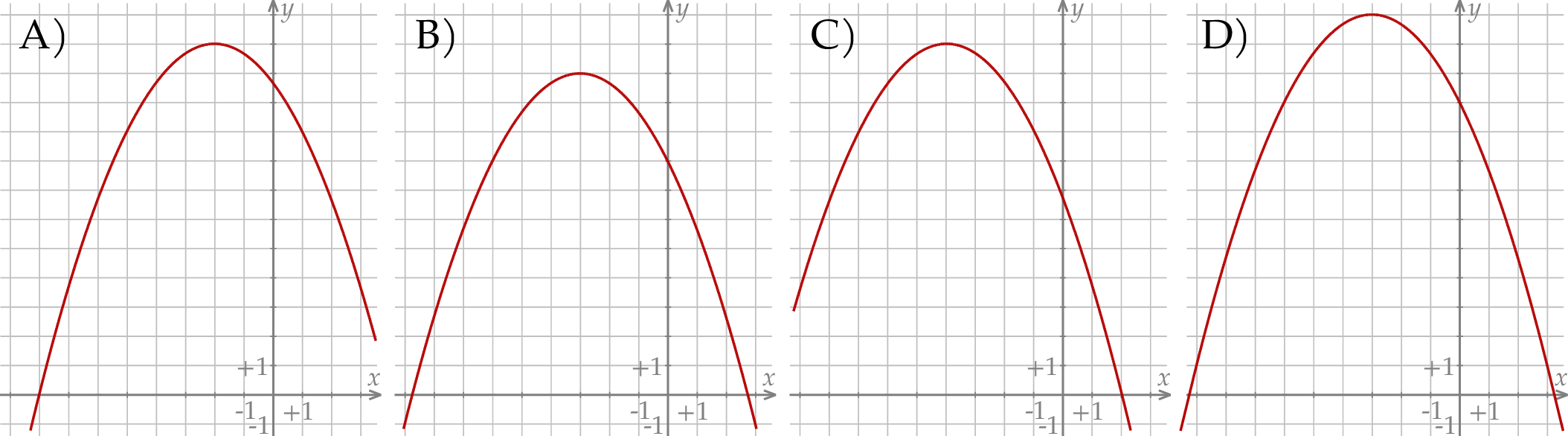
Na jednym z poniższych rysunków przedstawiono fragment wykresu funkcji 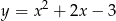 . Wskaż ten rysunek.
. Wskaż ten rysunek.
Na jednym z poniższych rysunków przedstawiono fragment wykresu funkcji 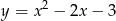 . Wskaż ten rysunek.
. Wskaż ten rysunek.
Wykres funkcji 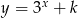 przechodzi przez punkt
przechodzi przez punkt 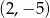 gdy liczba
gdy liczba 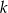 jest równa
jest równa
A) 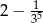 B) 4 C) -14 D) 14
B) 4 C) -14 D) 14
Jeżeli wiadomo, że punkt 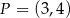 należy do wykresu funkcji
należy do wykresu funkcji 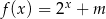 , to
, to
A) 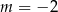 B)
B) 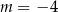 C)
C) 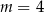 D)
D) 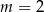
Wykres funkcji liniowej 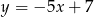 przecina pionową prostą przechodzącą przez punkt
przecina pionową prostą przechodzącą przez punkt 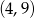 w punkcie o współrzędnych
w punkcie o współrzędnych
A) 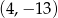 B)
B) 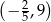 C)
C) 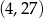 D)
D) 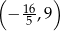
Wykres funkcji liniowej 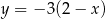 przecina prostą
przecina prostą 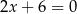 w punkcie
w punkcie
A) 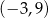 B)
B) 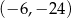 C)
C) 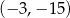 D)
D) 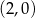
Wykres funkcji liniowej określonej wzorem 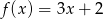 jest prostą prostopadłą do prostej o równaniu:
jest prostą prostopadłą do prostej o równaniu:
A) 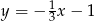 B)
B) 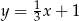 C)
C) 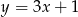 D)
D) 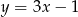
Wykres funkcji liniowej określonej wzorem 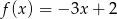 jest prostą prostopadłą do prostej o równaniu:
jest prostą prostopadłą do prostej o równaniu:
A) 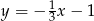 B)
B) 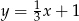 C)
C) 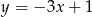 D)
D) 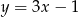
Wykres funkcji liniowej określonej wzorem 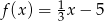 jest prostą prostopadłą do prostej o równaniu:
jest prostą prostopadłą do prostej o równaniu:
A) 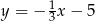 B)
B) 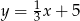 C)
C) 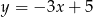 D)
D) 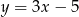
Wykres funkcji liniowej określonej wzorem 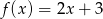 jest prostą prostopadłą do prostej o równaniu:
jest prostą prostopadłą do prostej o równaniu:
A) 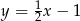 B)
B) 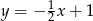 C)
C) 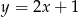 D)
D) 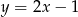
Proste 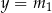 i
i 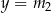 , gdzie
, gdzie 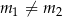 są styczne do wykresu funkcji
są styczne do wykresu funkcji 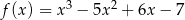 w punktach
w punktach 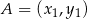 i
i 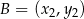 . Zatem
. Zatem
A) 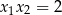 B)
B) 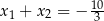 C)
C) 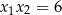 D)
D) 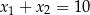
Punkt o współrzędnych 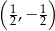 należy do wykresu funkcji logarytmicznej opisanej wzorem
należy do wykresu funkcji logarytmicznej opisanej wzorem
A) 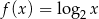 B)
B) 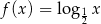 C)
C) 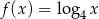 D)
D) 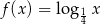
Na rysunku, w kartezjańskim układzie współrzędnych  , przedstawiono wykres funkcji
, przedstawiono wykres funkcji  określonej dla każdego
określonej dla każdego ![x ∈ (− 6,5]](https://img.zadania.info/zad/7384757/HzadT2x.gif) . Na tym wykresie zaznaczono punkty o współrzędnych całkowitych.
. Na tym wykresie zaznaczono punkty o współrzędnych całkowitych.
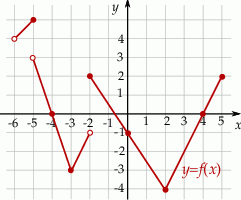
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Funkcja 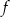 jest malejąca na przedziale jest malejąca na przedziale ![[− 2,2]](https://img.zadania.info/zad/7384757/HzadT5x.gif) . . | P | F |
Dla każdego argumentu z przedziału ![[− 4,− 2]](https://img.zadania.info/zad/7384757/HzadT6x.gif) funkcja funkcja 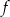 przyjmuje wartości niedodatnie. przyjmuje wartości niedodatnie. | P | F |
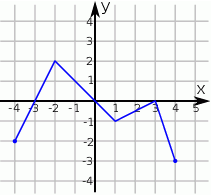
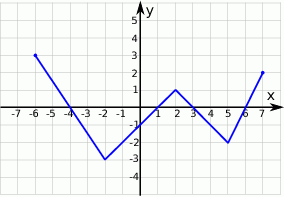
Rysunek przedstawia wykres pewnej funkcji 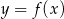 , określonej dla
, określonej dla 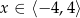 . Zbiór wszystkich argumentów, dla których funkcja
. Zbiór wszystkich argumentów, dla których funkcja 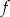 przyjmuje wartości niedodatnie, to zbiór:
przyjmuje wartości niedodatnie, to zbiór:
A) 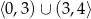 B)
B) 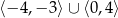
C) 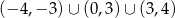 D)
D) 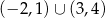
Na rysunku przedstawiony jest wykres pewnej funkcji 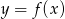 . Przyjmuje ona wartości niedodatnie dla argumentów:
. Przyjmuje ona wartości niedodatnie dla argumentów:
A) 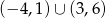 B)
B) 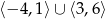 C)
C) 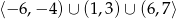 D)
D) 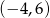
Na rysunku przedstawiono wykres funkcji 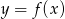 .
.
W którym z przedziałów, funkcja przyjmuje wartość 1?
A) 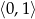 B)
B) 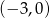 C)
C) 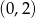 D)
D) 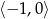
Dana jest funkcja kwadratowa 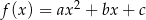 , gdzie
, gdzie 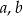 i
i  są liczbami rzeczywistymi takimi, że
są liczbami rzeczywistymi takimi, że 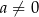 oraz
oraz 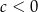 . Funkcja
. Funkcja 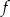 nie ma miejsc zerowych. Wykres funkcji
nie ma miejsc zerowych. Wykres funkcji 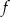 leży w całości
leży w całości
A) nad osią 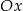 , , | B) pod osią 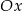 , , |
| ponieważ | |
| 1) | 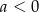 i i 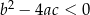 . . |
| 2) | 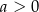 i i 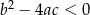 . . |
| 3) | 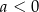 i i 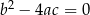 . . |
Dana jest funkcja kwadratowa 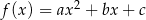 , gdzie
, gdzie 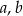 i
i  są liczbami rzeczywistymi takimi, że
są liczbami rzeczywistymi takimi, że 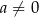 oraz
oraz 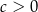 . Funkcja
. Funkcja 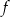 nie ma miejsc zerowych. Wykres funkcji
nie ma miejsc zerowych. Wykres funkcji 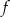 leży w całości
leży w całości
A) nad osią 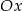 , , | B) pod osią 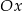 , , |
| ponieważ | |
| 1) | 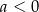 i i 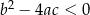 . . |
| 2) | 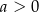 i i 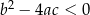 . . |
| 3) | 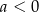 i i 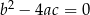 . . |
W kartezjańskim układzie współrzędnych 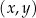 narysowano wykres funkcji
narysowano wykres funkcji 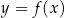 (zobacz rysunek).
(zobacz rysunek).
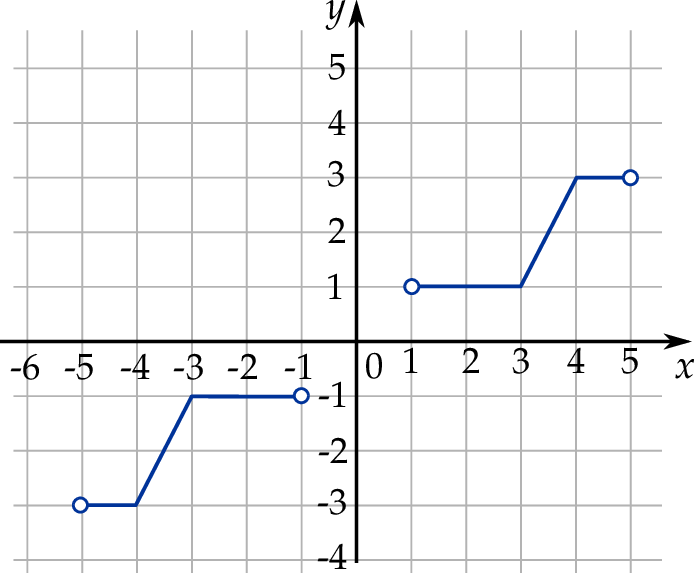
Zbiorem wartości funkcji 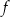 jest zbiór
jest zbiór
A) ![[− 3,− 1]∪ [1,3]](https://img.zadania.info/zad/7474248/HzadT4x.png) B)
B) 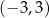 C)
C) 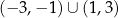
D) ![[− 5,− 1]∪ [1,5]](https://img.zadania.info/zad/7474248/HzadT7x.png) E)
E) 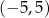 F)
F) 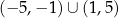
W kartezjańskim układzie współrzędnych 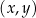 narysowano wykres funkcji
narysowano wykres funkcji 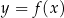 (zobacz rysunek).
(zobacz rysunek).
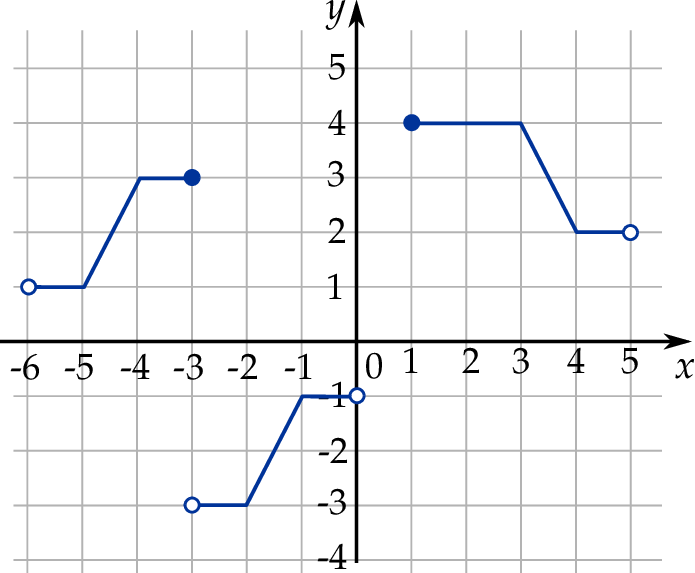
Zbiorem wartości funkcji  jest zbiór
jest zbiór
A)  B)
B) ![[− 3,4]](https://img.zadania.info/zad/5016823/HzadT5x.png) C)
C) 
D) ![[− 3,− 1)∪ (1 ,4 ]](https://img.zadania.info/zad/5016823/HzadT7x.png) E)
E) ![(− 3,4 ]](https://img.zadania.info/zad/5016823/HzadT8x.png) F)
F) ![[− 3,− 1] ∪ [1 ,4 ]](https://img.zadania.info/zad/5016823/HzadT9x.png)
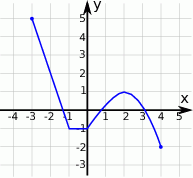
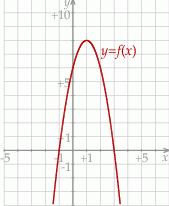
Dana jest funkcja kwadratowa 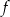 , której fragment wykresu przedstawiono w kartezjańskim układzie współrzędnych
, której fragment wykresu przedstawiono w kartezjańskim układzie współrzędnych 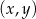 na rysunku poniżej. Wierzchołek paraboli, która jest wykresem funkcji
na rysunku poniżej. Wierzchołek paraboli, która jest wykresem funkcji 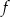 , oraz punkty przecięcia paraboli z osiami układu współrzędnych mają współrzędne całkowite.
, oraz punkty przecięcia paraboli z osiami układu współrzędnych mają współrzędne całkowite.
Funkcja 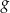 jest określona za pomocą funkcji
jest określona za pomocą funkcji 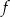 następująco:
następująco: 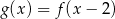 . Wykres funkcji
. Wykres funkcji 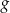 przedstawiono na rysunku
przedstawiono na rysunku
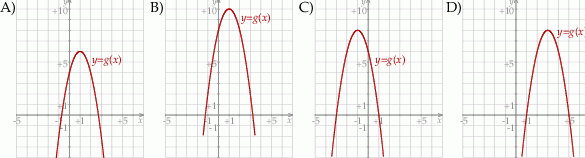
W kartezjańskim układzie współrzędnych 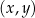 przedstawiono fragment wykresu funkcji kwadratowej
przedstawiono fragment wykresu funkcji kwadratowej 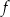 (zobacz rysunek). Wierzchołek paraboli, która jest wykresem funkcji
(zobacz rysunek). Wierzchołek paraboli, która jest wykresem funkcji 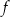 , oraz punkty przecięcia paraboli z osiami układu współrzędnych mają współrzędne całkowite.
, oraz punkty przecięcia paraboli z osiami układu współrzędnych mają współrzędne całkowite.
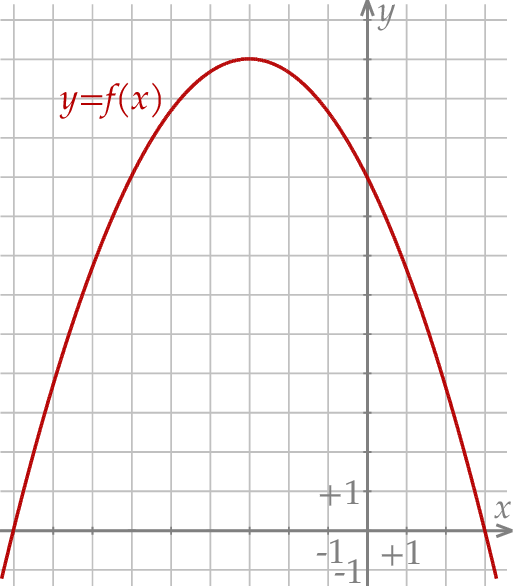
Funkcja kwadratowa  jest określona za pomocą funkcji
jest określona za pomocą funkcji  następująco:
następująco: 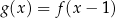 . Fragment wykresu funkcji
. Fragment wykresu funkcji 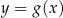 przedstawiono na rysunku
przedstawiono na rysunku
W kartezjańskim układzie współrzędnych  przedstawiono fragment wykresu funkcji kwadratowej
przedstawiono fragment wykresu funkcji kwadratowej  (zobacz rysunek). Wierzchołek paraboli, która jest wykresem funkcji
(zobacz rysunek). Wierzchołek paraboli, która jest wykresem funkcji 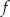 , oraz punkty przecięcia paraboli z osiami układu współrzędnych mają współrzędne całkowite.
, oraz punkty przecięcia paraboli z osiami układu współrzędnych mają współrzędne całkowite.
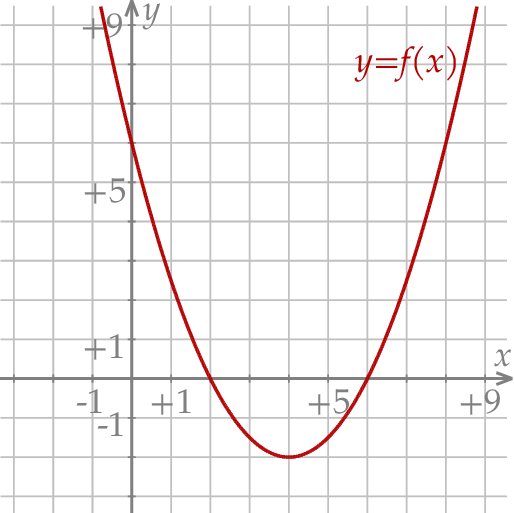
Funkcja kwadratowa 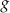 jest określona za pomocą funkcji
jest określona za pomocą funkcji 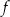 następująco:
następująco: 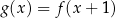 . Fragment wykresu funkcji
. Fragment wykresu funkcji  przedstawiono na rysunku
przedstawiono na rysunku
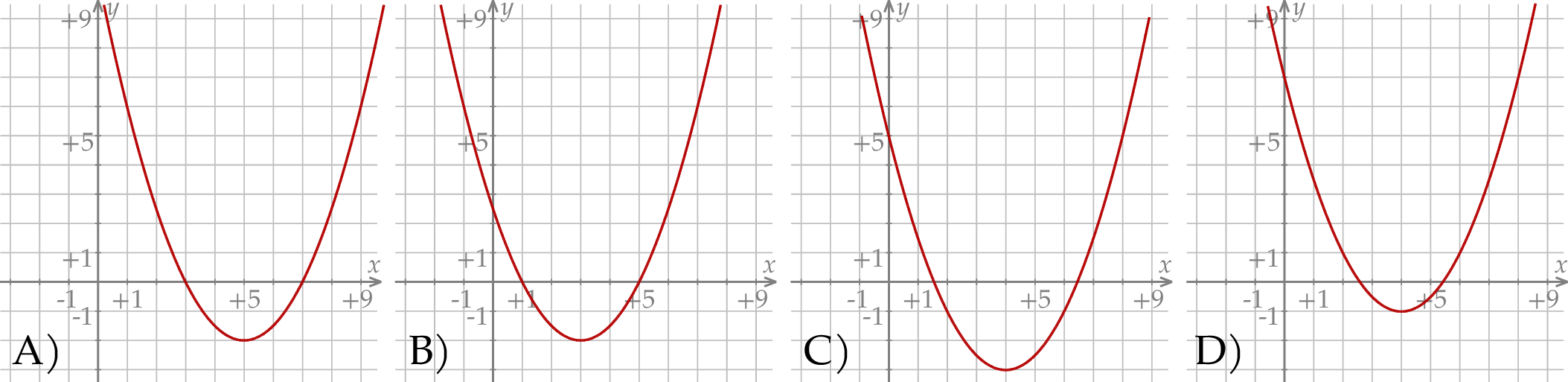
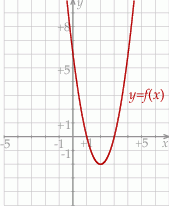
Dana jest funkcja kwadratowa  , której fragment wykresu przedstawiono na rysunku poniżej. Wierzchołek paraboli, która jest wykresem funkcji
, której fragment wykresu przedstawiono na rysunku poniżej. Wierzchołek paraboli, która jest wykresem funkcji 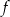 , oraz punkty przecięcia paraboli z osiami układu współrzędnych mają współrzędne całkowite.
, oraz punkty przecięcia paraboli z osiami układu współrzędnych mają współrzędne całkowite.
Funkcja 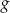 jest określona za pomocą funkcji
jest określona za pomocą funkcji 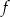 następująco:
następująco: 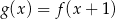 . Wykres funkcji
. Wykres funkcji 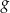 przedstawiono na rysunku
przedstawiono na rysunku
Parabola o wierzchołku 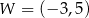 i ramionach skierowanych w dół może być wykresem funkcji określonej wzorem
i ramionach skierowanych w dół może być wykresem funkcji określonej wzorem
A) 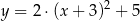 B)
B) 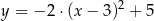
C) 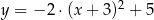 D)
D) 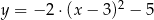
Punkt 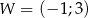 jest wierzchołkiem wykresu funkcji kwadratowej
jest wierzchołkiem wykresu funkcji kwadratowej 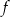 . Wobec tego funkcję
. Wobec tego funkcję 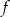 może przedstawiać wzór
może przedstawiać wzór
A) 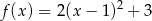 B)
B) 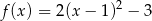
C) 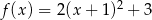 D)
D) 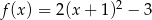
Parabola o wierzchołku 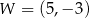 i ramionach skierowanych w dół może być wykresem funkcji określonej wzorem
i ramionach skierowanych w dół może być wykresem funkcji określonej wzorem
A) 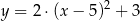 B)
B) 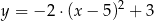
C) 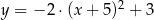 D)
D)