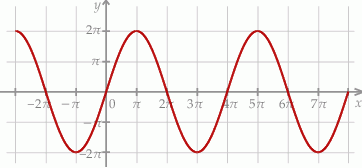
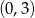Na rysunku przedstawiono fragment wykresu pewnej funkcji 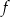 określonej dla każdej liczby rzeczywistej
określonej dla każdej liczby rzeczywistej  . Jeden z podanych poniżej wzorów jest wzorem tej funkcji. Wskaż wzór funkcji
. Jeden z podanych poniżej wzorów jest wzorem tej funkcji. Wskaż wzór funkcji 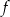 .
.
A) 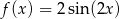 B)
B) 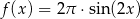
C) 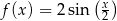 D)
D) 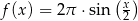
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Na rysunku przedstawiono fragment wykresu pewnej funkcji  określonej dla każdej liczby rzeczywistej
określonej dla każdej liczby rzeczywistej  . Jeden z podanych poniżej wzorów jest wzorem tej funkcji. Wskaż wzór funkcji
. Jeden z podanych poniżej wzorów jest wzorem tej funkcji. Wskaż wzór funkcji 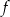 .
.

A) 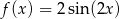 B)
B) 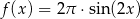
C) 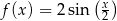 D)
D) 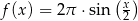
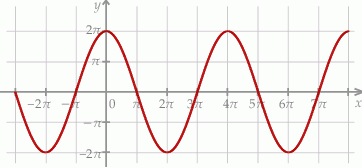
Na rysunku przedstawiono fragment wykresu pewnej funkcji 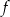 określonej dla każdej liczby rzeczywistej
określonej dla każdej liczby rzeczywistej  . Jeden z podanych poniżej wzorów jest wzorem tej funkcji. Wskaż wzór funkcji
. Jeden z podanych poniżej wzorów jest wzorem tej funkcji. Wskaż wzór funkcji  .
.
A) 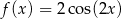 B)
B) 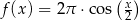
C) 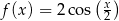 D)
D) 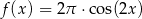
Na rysunku przedstawiono fragment wykresu pewnej funkcji 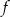 . Jeden z podanych poniżej wzorów jest wzorem tej funkcji. Wskaż wzór funkcji
. Jeden z podanych poniżej wzorów jest wzorem tej funkcji. Wskaż wzór funkcji 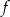 .
.
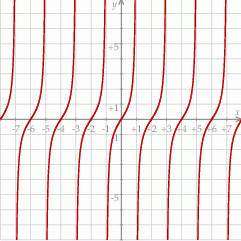
A) 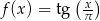 B)
B) 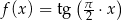
C) 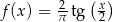 D)
D) 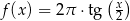
Wykresem funkcji kwadratowej 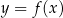 jest parabola o wierzchołku w punkcie
jest parabola o wierzchołku w punkcie 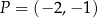 . Prosta
. Prosta 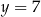 przecina tę parabolę w punktach
przecina tę parabolę w punktach 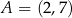 i
i 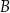 . Długość odcinka
. Długość odcinka 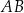 jest równa
jest równa
A) 18 B) 6 C) 10 D) 8
Funkcja liniowa, której wykres jest równoległy do wykresu funkcji 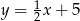 ma wzór:
ma wzór:
A) 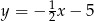 B)
B) 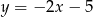 C)
C) 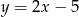 D)
D) 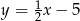
Wykresem funkcji 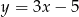 jest prosta równoległa do wykresu funkcji
jest prosta równoległa do wykresu funkcji
A) 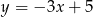 B)
B) 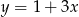 C)
C) 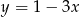 D)
D) 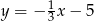
Na rysunku przedstawiony jest wykres funkcji 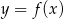 . Dziedziną funkcji
. Dziedziną funkcji 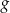 , gdzie
, gdzie 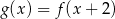 jest zbiór
jest zbiór
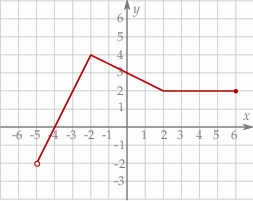
A) 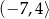 B)
B) 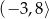 C)
C) 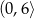 D)
D) 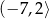
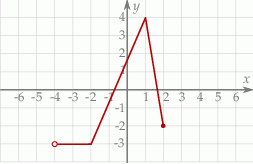
Na rysunku przedstawiony jest wykres funkcji 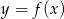 . Dziedziną funkcji
. Dziedziną funkcji 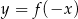 jest
jest
A) 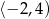 B)
B) 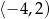 C)
C) 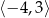 D)
D) 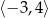
Na rysunku przedstawiony jest wykres funkcji 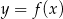 . Dziedziną funkcji
. Dziedziną funkcji 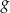 , gdzie
, gdzie 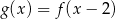 jest zbiór
jest zbiór
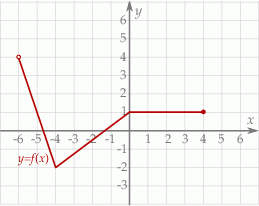
A) 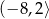 B)
B) 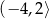 C)
C) 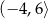 D)
D) 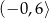
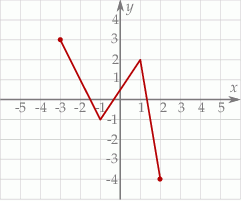
Jeśli na rysunku przedstawiony jest wykres funkcji 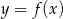 , to dziedziną funkcji
, to dziedziną funkcji 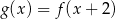 jest zbiór
jest zbiór
A) 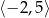 B)
B) 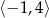 C)
C) 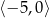 D)
D) 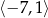
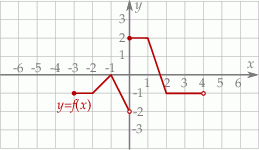
Jeśli na rysunku przedstawiony jest wykres funkcji 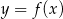 , to dziedziną funkcji
, to dziedziną funkcji 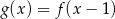 jest zbiór
jest zbiór
A) 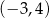 B)
B) 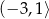 C)
C) 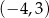 D)
D) 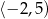
Dana jest funkcja 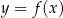 określona dla
określona dla 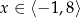 , której wykres jest przedstawiony na rysunku.
, której wykres jest przedstawiony na rysunku.
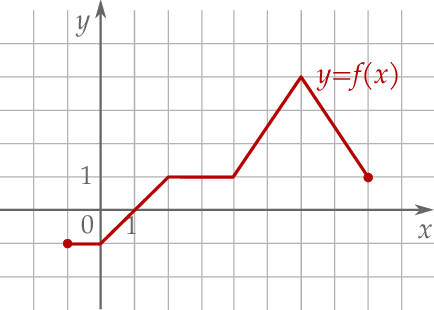
Wskaż zbiór wartości tej funkcji.
A) 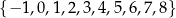 B)
B) 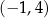 C)
C) 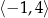 D)
D) 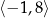
Na rysunku przedstawiono wykres funkcji 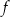 .
.
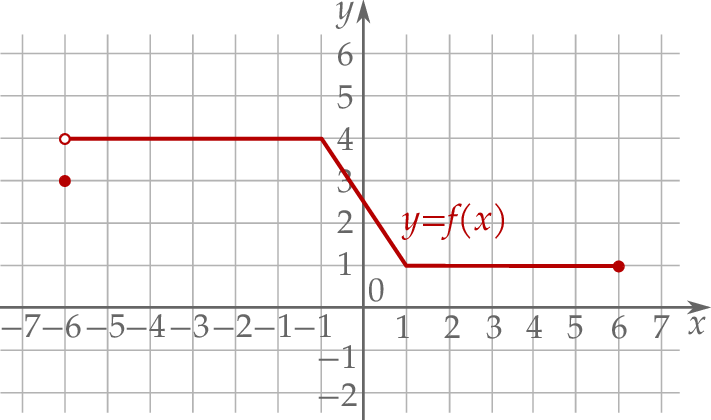
Zbiorem wartości tej funkcji jest
A) ![(− 6,6]](https://img.zadania.info/zad/5671019/HzadT2x.png) B)
B) 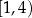 C)
C) ![[1,4]](https://img.zadania.info/zad/5671019/HzadT4x.png) D)
D) ![[− 6,6]](https://img.zadania.info/zad/5671019/HzadT5x.png)
Zbiorem wartości funkcji 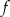 , której wykres przedstawiono poniżej jest
, której wykres przedstawiono poniżej jest
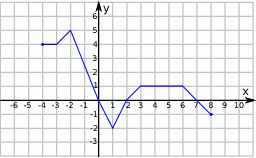
A) 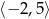 B)
B) 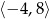 C)
C) 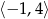 D)
D) 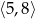
Dana jest funkcja 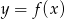 , której wykres jest przedstawiony na rysunku.
, której wykres jest przedstawiony na rysunku.
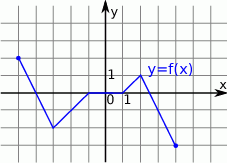
Wskaż zbiór wartości tej funkcji.
A) 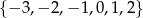 B)
B) 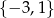 C)
C) 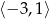 D)
D) 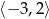
Zbiorem wartości funkcji 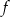 , której wykres przedstawiono poniżej jest
, której wykres przedstawiono poniżej jest
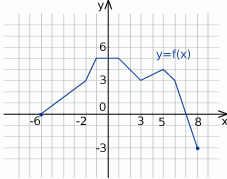
A) 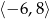 B)
B) 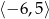 C)
C) 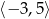 D)
D) 
Zbiorem wartości funkcji 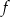 , której wykres przedstawiono na wykresie poniżej jest przedział
, której wykres przedstawiono na wykresie poniżej jest przedział
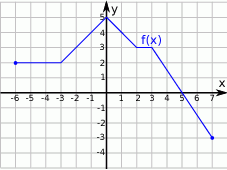
A)  B)
B) 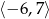 C)
C) 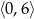 D)
D) 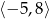
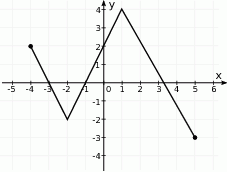
Zbiorem wartości funkcji, której wykres przedstawiono na rysunku jest przedział:
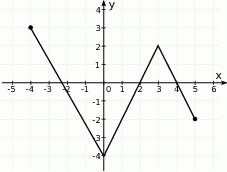
A) 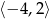 B)
B) 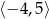 C)
C) 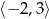 D)
D) 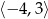
Zbiorem wartości funkcji, której wykres przedstawiono na rysunku jest przedział:
A) 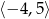 B)
B) 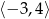 C)
C) 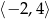 D)
D) 
Funkcja kwadratowa 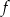 jest określona wzorem
jest określona wzorem 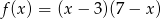 . Wierzchołek paraboli będącej wykresem funkcji
. Wierzchołek paraboli będącej wykresem funkcji 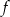 należy do prostej o równaniu
należy do prostej o równaniu
A) 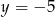 B)
B) 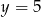 C)
C) 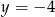 D)
D) 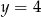
Funkcja kwadratowa 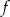 jest określona wzorem
jest określona wzorem 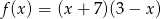 . Wierzchołek paraboli będącej wykresem funkcji
. Wierzchołek paraboli będącej wykresem funkcji 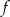 należy do prostej o równaniu
należy do prostej o równaniu
A) 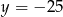 B)
B) 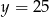 C)
C) 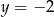 D)
D) 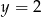
Na rysunku przedstawiony jest fragment paraboli będącej wykresem funkcji kwadratowej 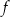 . Wierzchołkiem tej paraboli jest punkt
. Wierzchołkiem tej paraboli jest punkt 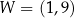 . Liczby
. Liczby 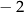 i 4 to miejsca zerowe funkcji
i 4 to miejsca zerowe funkcji 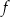 .
.
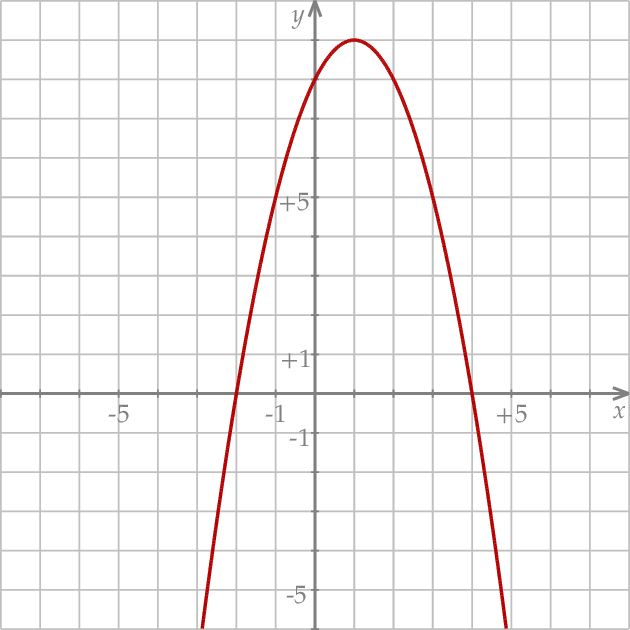
Najmniejsza wartość funkcji 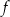 w przedziale
w przedziale 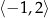 jest równa
jest równa
A) 2 B) 5 C) 8 D) 9
Funkcja kwadratowa 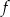 jest określona wzorem
jest określona wzorem 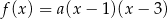 . Na rysunku przedstawiono fragment paraboli będącej wykresem tej funkcji. Wierzchołkiem tej paraboli jest punkt
. Na rysunku przedstawiono fragment paraboli będącej wykresem tej funkcji. Wierzchołkiem tej paraboli jest punkt 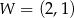 .
.
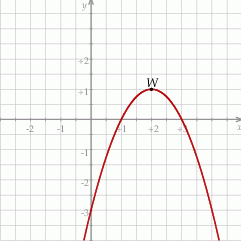
Największa wartość funkcji 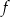 w przedziale
w przedziale 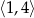 jest równa
jest równa
A) 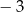 B) 0 C) 1 D) 2
B) 0 C) 1 D) 2
Na rysunku przedstawiony jest fragment paraboli będącej wykresem funkcji kwadratowej 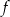 . Wierzchołkiem tej paraboli jest punkt
. Wierzchołkiem tej paraboli jest punkt 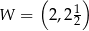 . Liczby
. Liczby 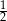 i
i 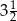 to miejsca zerowe funkcji
to miejsca zerowe funkcji 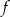 .
.
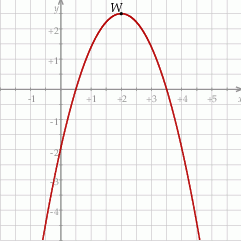
Najmniejsza wartość funkcji 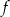 w przedziale
w przedziale 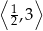 jest równa
jest równa
A) 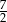 B)
B) 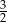 C) 0 D)
C) 0 D) 
Na rysunku przedstawiony jest fragment paraboli będącej wykresem funkcji kwadratowej 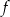 . Wierzchołkiem tej paraboli jest punkt
. Wierzchołkiem tej paraboli jest punkt 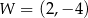 . Liczby 0 i 4 to miejsca zerowe funkcji
. Liczby 0 i 4 to miejsca zerowe funkcji 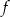 .
.
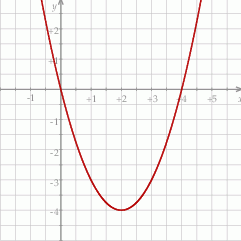
Największa wartość funkcji 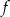 w przedziale
w przedziale 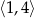 jest równa
jest równa
A) 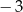 B)
B) 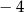 C) 4 D) 0
C) 4 D) 0
Funkcja kwadratowa 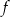 jest określona wzorem
jest określona wzorem 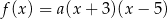 . Na rysunku przedstawiono fragment paraboli będącej wykresem tej funkcji. Wierzchołkiem tej paraboli jest punkt
. Na rysunku przedstawiono fragment paraboli będącej wykresem tej funkcji. Wierzchołkiem tej paraboli jest punkt 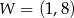 .
.
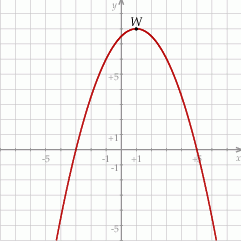
Największa wartość funkcji 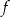 w przedziale
w przedziale 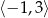 jest równa
jest równa
A) 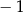 B) 0 C) 8 D) 6
B) 0 C) 8 D) 6
Na rysunku przedstawiony jest fragment paraboli będącej wykresem funkcji kwadratowej 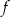 . Wierzchołkiem tej paraboli jest punkt
. Wierzchołkiem tej paraboli jest punkt 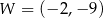 . Liczby
. Liczby 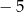 i 1 to miejsca zerowe funkcji
i 1 to miejsca zerowe funkcji 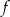 .
.
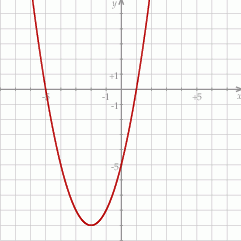
Największa wartość funkcji 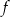 w przedziale
w przedziale 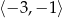 jest równa
jest równa
A) 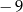 B)
B) 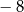 C)
C) 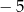 D) 0
D) 0
Wykres funkcji liniowej 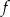 przecina osie układu współrzędnych w punktach
przecina osie układu współrzędnych w punktach 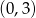 i
i 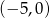 . Wynika stąd, że
. Wynika stąd, że
A) 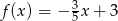 B)
B) 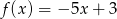 C)
C) 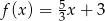 D)
D) 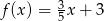
Dana jest funkcja wykładnicza 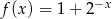 określona dla
określona dla 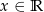 . Zbiorem wartości funkcji
. Zbiorem wartości funkcji 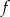 jest przedział
jest przedział
A) 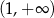 , , | B) 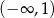 , , |
ponieważ wykres funkcji 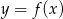 można otrzymać z wykresu funkcji
można otrzymać z wykresu funkcji 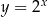 poprzez
poprzez
| 1) | symetrię względem osi 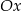 i przesunięcie o 1 jednostkę w dół. i przesunięcie o 1 jednostkę w dół. |
| 2) | symetrię względem osi 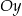 i przesunięcie o 1 jednostkę w górę. i przesunięcie o 1 jednostkę w górę. |
| 3) | symetrię względem osi 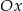 i przesunięcie o 1 jednostkę w górę. i przesunięcie o 1 jednostkę w górę. |
Punkt 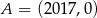 należy do wykresu funkcji
należy do wykresu funkcji 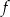 określonej wzorem
określonej wzorem
A) 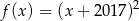 B)
B) 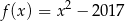
C) 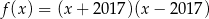 D)
D) 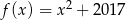
Punkt 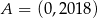 należy do wykresu funkcji
należy do wykresu funkcji 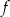 określonej wzorem
określonej wzorem
A) 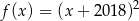 B)
B) 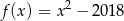
C) 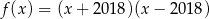 D)
D) 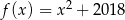
Na rysunku, w kartezjańskim układzie współrzędnych 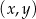 , przedstawiono wykres funkcji
, przedstawiono wykres funkcji 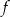 określonej dla każdego
określonej dla każdego 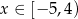 . Na tym wykresie zaznaczono punkty o współrzędnych całkowitych.
. Na tym wykresie zaznaczono punkty o współrzędnych całkowitych.
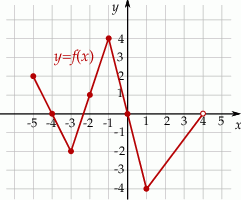
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Dla każdego argumentu z przedziału 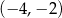 funkcja funkcja 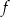 przyjmuje wartości ujemne. przyjmuje wartości ujemne. | P | F |
Funkcja 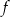 ma trzy miejsca zerowe. ma trzy miejsca zerowe. | P | F |
Na rysunku, w kartezjańskim układzie współrzędnych 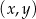 , przedstawiono wykres funkcji
, przedstawiono wykres funkcji 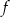 określonej dla każdego
określonej dla każdego ![x ∈ (− 4,5]](https://img.zadania.info/zad/8434319/HzadT2x.gif) . Na tym wykresie zaznaczono punkty o współrzędnych całkowitych.
. Na tym wykresie zaznaczono punkty o współrzędnych całkowitych.
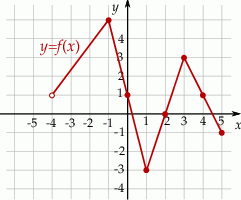
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Dla każdego argumentu z przedziału 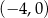 funkcja funkcja 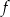 przyjmuje wartości dodatnie. przyjmuje wartości dodatnie. | P | F |
Funkcja 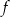 ma cztery miejsca zerowe. ma cztery miejsca zerowe. | P | F |
Na poniższym rysunku przedstawiono wykres funkcji 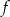 określonej w zbiorze
określonej w zbiorze 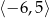 .
.
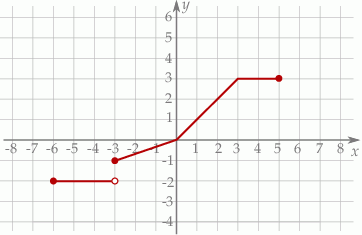
Funkcja 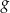 jest określona wzorem
jest określona wzorem 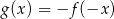 dla
dla 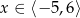 . Wskaż zdanie prawdziwe.
. Wskaż zdanie prawdziwe.
A) Zbiór wartości funkcji 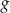 nie zawiera liczb dodatnich.
nie zawiera liczb dodatnich.
B) Punkt 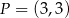 należy do wykresów funkcji
należy do wykresów funkcji 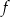 i
i 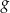 .
.
C) Równanie 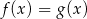 ma nieskończenie wiele rozwiązań.
ma nieskończenie wiele rozwiązań.
D) Jest tylko jedna liczba  spełniająca nierówność
spełniająca nierówność 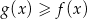 .
.
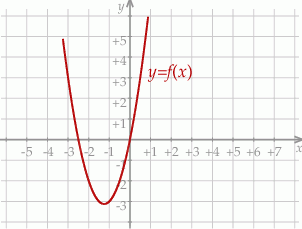
Na rysunku przedstawiono fragment wykresu funkcji kwadratowej 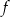 określonej wzorem
określonej wzorem 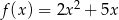 .
.
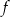 jest prosta o równaniu
jest prosta o równaniu 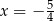 B)
B) 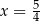 C)
C) 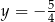 D)
D) 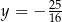
Wykres funkcji liniowej 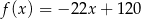 przechodzi przez ćwiartki układu współrzędnych:
przechodzi przez ćwiartki układu współrzędnych:
A) I, II, III B) I, II, IV C) I, III, IV D) II, III, IV
Funkcja kwadratowa 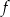 jest określona wzorem
jest określona wzorem 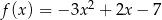 . Jeżeli przesuniemy wykres funkcji
. Jeżeli przesuniemy wykres funkcji 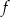 o dwie jednostki 2 lewo, to otrzymamy wykres funkcji
o dwie jednostki 2 lewo, to otrzymamy wykres funkcji
A) 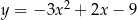 B)
B) 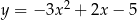
C) 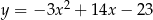 D)
D) 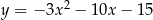
Odległość wierzchołka paraboli 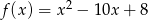 od osi
od osi 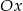 jest równa
jest równa
A) 5 B) 17 C) 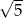 D)
D) 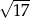
Odległość wierzchołka paraboli 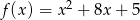 od osi
od osi 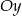 jest równa
jest równa
A) -11 B) 11 C) 4 D) 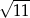
Odległość wierzchołka paraboli 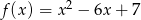 od osi
od osi 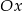 jest równa
jest równa
A) 2 B) -2 C) 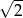 D) 3
D) 3
Wykres funkcji kwadratowej 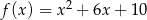 powstaje z wykresu funkcji
powstaje z wykresu funkcji 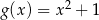 przez przesunięcie o 3 jednostki
przez przesunięcie o 3 jednostki
A) w prawo B) w lewo C) w górę D) w dół
Wykres funkcji kwadratowej 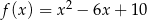 powstaje z wykresu funkcji
powstaje z wykresu funkcji 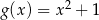 przez przesunięcie o 3 jednostki
przez przesunięcie o 3 jednostki
A) w prawo B) w lewo C) w górę D) w dół
Na rysunku przedstawiony jest fragment wykresu funkcji liniowej 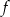 , przy czym
, przy czym 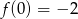 i
i 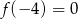 .
.
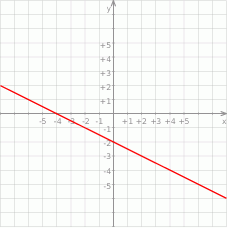
Wykres funkcji 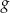 jest symetryczny do wykresu funkcji
jest symetryczny do wykresu funkcji 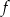 względem prostej
względem prostej 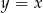 . Funkcja
. Funkcja 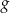 jest określona wzorem
jest określona wzorem
A) 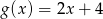 B)
B) 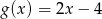 C)
C) 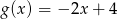 D)
D) 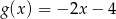
W kartezjańskim układzie współrzędnych 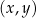 przedstawiono fragment paraboli, która jest wykresem funkcji kwadratowej
przedstawiono fragment paraboli, która jest wykresem funkcji kwadratowej 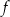 (zobacz rysunek). Wierzchołek tej paraboli oraz punkty przecięcia paraboli z osiami układu współrzędnych mają obie współrzędne całkowite.
(zobacz rysunek). Wierzchołek tej paraboli oraz punkty przecięcia paraboli z osiami układu współrzędnych mają obie współrzędne całkowite.
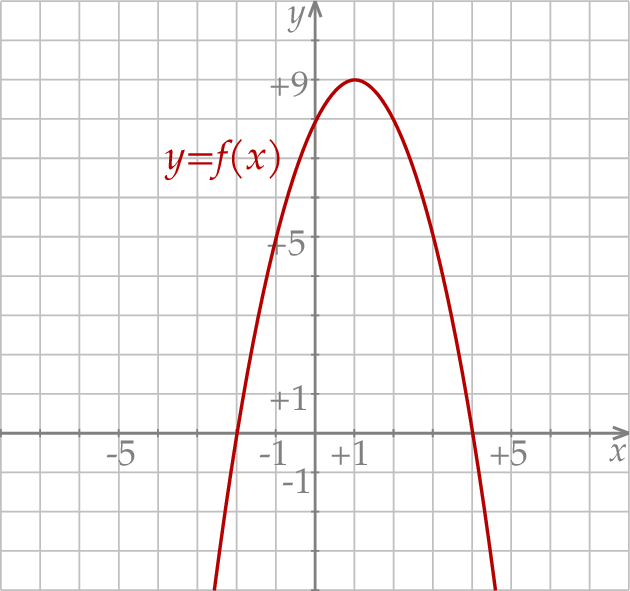
Dla funkcji 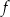 prawdziwa jest równość
prawdziwa jest równość
A) 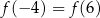 B)
B) 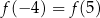 C)
C) 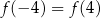 D)
D) 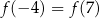
Wykres funkcji liniowej 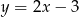 przecina oś
przecina oś 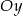 w punkcie o współrzędnych
w punkcie o współrzędnych
A) 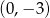 B)
B) 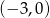 C)
C) 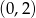 D)
D) 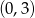
Wykres funkcji liniowej 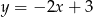 przecina oś
przecina oś 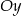 w punkcie o współrzędnych
w punkcie o współrzędnych
A) 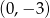 B)
B) 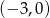 C)
C) 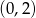 D)
D)