Funkcja 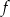 określona jest wzorem
określona jest wzorem 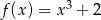 . Wykres funkcji
. Wykres funkcji 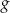 powstaje z wykresu funkcji
powstaje z wykresu funkcji 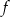 przez przesunięcie o jedną jednostkę w prawo wzdłuż osi
przez przesunięcie o jedną jednostkę w prawo wzdłuż osi 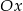 . Punkt
. Punkt 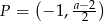 należy do wykresu funkcji
należy do wykresu funkcji 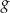 , gdy liczba
, gdy liczba  jest równa
jest równa
A) 2 B) -2 C) 22 D) -10
/Szkoła średnia/Zadania testowe/Funkcje - wykresy
Funkcja 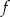 określona jest wzorem
określona jest wzorem 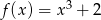 . Wykres funkcji
. Wykres funkcji  powstaje z wykresu funkcji
powstaje z wykresu funkcji  przez przesunięcie o jedną jednostkę w lewo wzdłuż osi
przez przesunięcie o jedną jednostkę w lewo wzdłuż osi 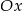 . Punkt
. Punkt 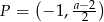 należy do wykresu funkcji
należy do wykresu funkcji 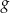 , gdy liczba
, gdy liczba  jest równa
jest równa
A) 6 B) -2 C) 22 D) -10
Funkcja 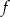 określona jest wzorem
określona jest wzorem 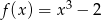 . Wykres funkcji
. Wykres funkcji 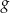 powstaje z wykresu funkcji
powstaje z wykresu funkcji 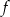 przez przesunięcie o jedną jednostkę w prawo wzdłuż osi
przez przesunięcie o jedną jednostkę w prawo wzdłuż osi 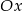 . Punkt
. Punkt 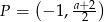 należy do wykresu funkcji
należy do wykresu funkcji  , gdy liczba
, gdy liczba  jest równa
jest równa
A) 2 B) -2 C) -22 D) -10
Gdy przesuniemy wykres funkcji 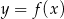 o 2 jednostki w prawo i o 3 jednostki w górę, to otrzymamy wykres funkcji
o 2 jednostki w prawo i o 3 jednostki w górę, to otrzymamy wykres funkcji 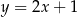 . Zatem
. Zatem
A) 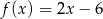 B)
B) 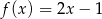 C)
C) 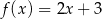 D)
D) 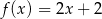
Gdy przesuniemy wykres funkcji 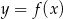 o 2 jednostki w lewo i o 3 jednostki w dół, to otrzymamy wykres funkcji
o 2 jednostki w lewo i o 3 jednostki w dół, to otrzymamy wykres funkcji 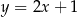 . Zatem
. Zatem
A) 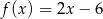 B)
B) 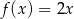 C)
C) 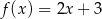 D)
D) 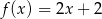
Na rysunku przedstawiony jest wykres funkcji 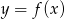 .
.
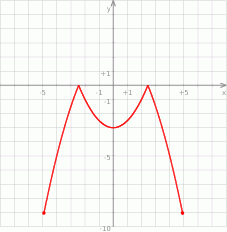
Które z równań ma dokładnie trzy rozwiązania?
A) 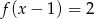 B)
B) 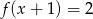 C)
C) 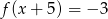 D)
D) 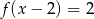
Na rysunku przedstawiony jest wykres funkcji 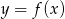 .
.
Które z równań ma dokładnie trzy rozwiązania?
A) 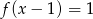 B)
B) 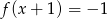 C)
C) 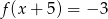 D)
D) 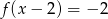
Na rysunku 1 jest przedstawiony wykres funkcji 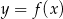 .
.
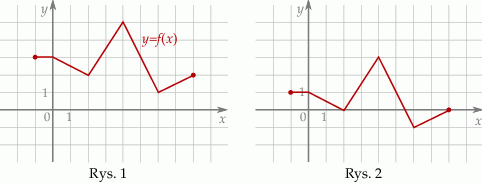
Funkcja przedstawiona na rysunku 2 jest określona wzorem
A) 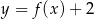 B)
B) 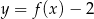 C)
C) 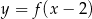 D)
D) 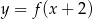
Na rysunku 1 jest przedstawiony wykres funkcji 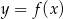 .
.
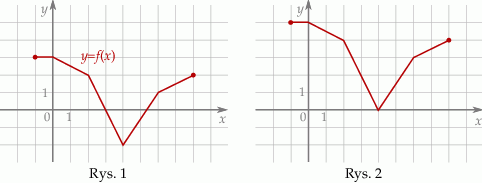
Funkcja przedstawiona na rysunku 2 jest określona wzorem
A) 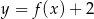 B)
B) 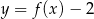 C)
C) 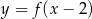 D)
D) 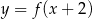
Na poniższych rysunkach przedstawiono wykresy funkcji 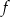 i
i 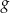 .
.
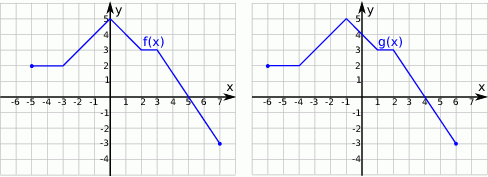
Funkcja 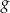 jest określona wzorem
jest określona wzorem
A) 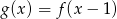 B)
B) 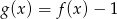 C)
C) 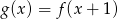 D)
D) 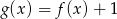
Na poniższych rysunkach przedstawiono wykresy funkcji 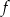 i
i 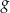 .
.
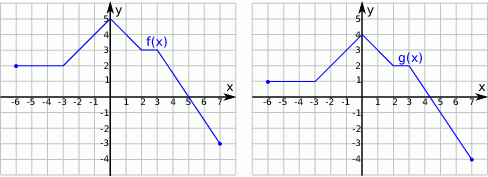
Funkcja 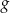 jest określona wzorem
jest określona wzorem
A) 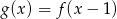 B)
B) 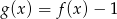 C)
C) 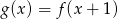 D)
D) 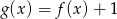
Styczna do wykresu funkcji 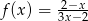 w punkcie o współrzędnych
w punkcie o współrzędnych 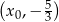 ma równanie
ma równanie
A) 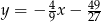 B)
B) 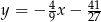 C)
C) 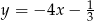 D)
D) 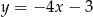
Wierzchołek paraboli 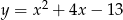 leży na prostej o równaniu
leży na prostej o równaniu
A) 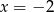 B)
B) 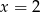 C)
C) 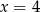 D)
D) 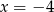
Wierzchołek paraboli 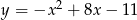 leży na prostej o równaniu
leży na prostej o równaniu
A) 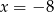 B)
B) 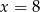 C)
C) 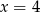 D)
D) 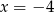
Wierzchołek paraboli 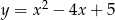 leży na prostej o równaniu
leży na prostej o równaniu
A) 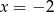 B)
B) 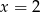 C)
C) 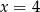 D)
D) 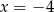
Wykresem funkcji kwadratowej 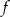 jest parabola o wierzchołku
jest parabola o wierzchołku 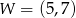 . Wówczas prawdziwa jest równość
. Wówczas prawdziwa jest równość
A) 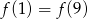 B)
B) 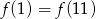 C)
C) 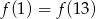 D)
D) 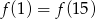
Wykresem funkcji kwadratowej  jest parabola o wierzchołku
jest parabola o wierzchołku 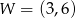 . Wówczas prawdziwa jest równość
. Wówczas prawdziwa jest równość
A) 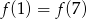 B)
B) 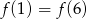 C)
C) 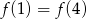 D)
D) 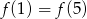
Wykresem funkcji kwadratowej 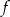 jest parabola o wierzchołku
jest parabola o wierzchołku 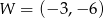 . Wówczas prawdziwa jest równość
. Wówczas prawdziwa jest równość
A) 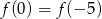 B)
B) 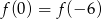 C)
C) 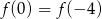 D)
D) 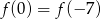
Wykresem funkcji kwadratowej 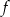 jest parabola o wierzchołku
jest parabola o wierzchołku 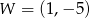 . Wówczas prawdziwa jest równość
. Wówczas prawdziwa jest równość
A) 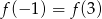 B)
B) 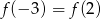 C)
C) 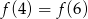 D)
D) 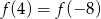
Na rysunku przedstawiono fragment wykresu pewnej funkcji liniowej 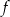 .
.
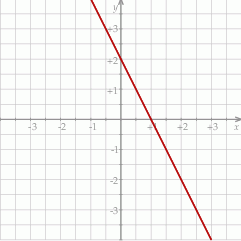
Funkcja liniowa 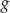 , której wykres jest symetryczny do wykresu funkcji
, której wykres jest symetryczny do wykresu funkcji 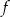 względem poziomej osi układu współrzędnych, jest określona wzorem
względem poziomej osi układu współrzędnych, jest określona wzorem
A) 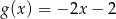 B)
B) 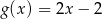 C)
C) 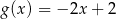 D)
D) 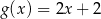
Na rysunku przedstawiony jest fragment wykresu funkcji liniowej 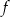 . Na wykresie tej funkcji leżą punkty
. Na wykresie tej funkcji leżą punkty 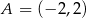 i
i 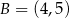 .
.
Obrazem prostej 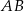 w symetrii względem początku układu współrzędnych jest wykres funkcji
w symetrii względem początku układu współrzędnych jest wykres funkcji 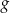 określonej wzorem
określonej wzorem
A) 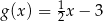 B)
B) 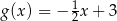 C)
C) 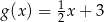 D)
D) 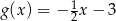
Na rysunku przedstawiony jest fragment wykresu funkcji liniowej 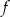 , przy czym
, przy czym 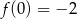 i
i 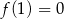 .
.
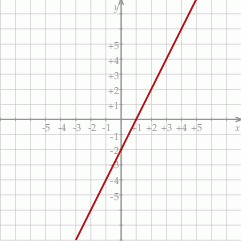
Wykres funkcji 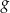 jest symetryczny do wykresu funkcji
jest symetryczny do wykresu funkcji 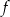 względem początku układu współrzędnych. Funkcja
względem początku układu współrzędnych. Funkcja 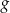 jest określona wzorem
jest określona wzorem
A) 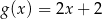 B)
B) 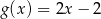 C)
C) 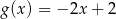 D)
D) 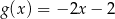
Na rysunku przedstawiony jest fragment wykresu funkcji liniowej 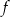 . Na wykresie tej funkcji leżą punkty
. Na wykresie tej funkcji leżą punkty 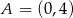 i
i 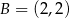 .
.
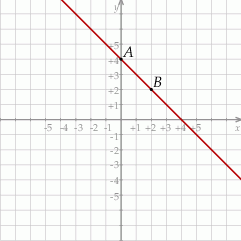
Obrazem prostej 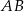 w symetrii względem początku układu współrzędnych jest wykres funkcji
w symetrii względem początku układu współrzędnych jest wykres funkcji 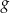 określonej wzorem
określonej wzorem
A) 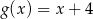 B)
B) 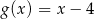 C)
C) 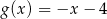 D)
D) 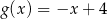
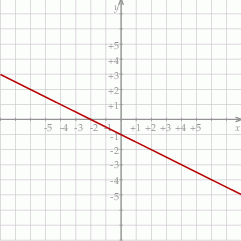
Na rysunku przedstawiony jest fragment wykresu funkcji liniowej 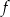 , przy czym
, przy czym 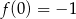 i
i 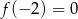 .
.
Wykres funkcji 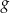 jest symetryczny do wykresu funkcji
jest symetryczny do wykresu funkcji 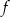 względem początku układu współrzędnych. Funkcja
względem początku układu współrzędnych. Funkcja 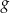 jest określona wzorem
jest określona wzorem
A) 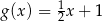 B)
B) 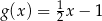 C)
C) 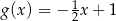 D)
D) 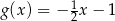
Na rysunku przedstawiono fragment wykresu funkcji kwadratowej 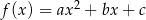 , której miejsca zerowe to:
, której miejsca zerowe to: 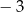 i 2. Do wykresu tego należy punkt
i 2. Do wykresu tego należy punkt 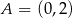 .
.
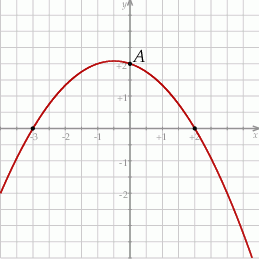
Współczynnik  we wzorze funkcji
we wzorze funkcji 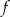 jest równy
jest równy
A) 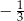 B)
B) 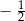 C)
C) 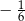 D)
D) 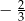
Liczba punktów wspólnych wykresów funkcji 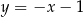 i
i 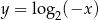 jest równa
jest równa
A) 0 B) 1 C) 2 D) 3
Do wykresu funkcji 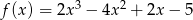 należy punkt o współrzędnych
należy punkt o współrzędnych
A) 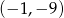 B)
B) 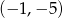 C)
C) 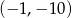 D)
D) 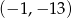
Do wykresu funkcji 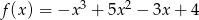 należy punkt o współrzędnych
należy punkt o współrzędnych
A) 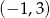 B)
B) 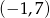 C)
C) 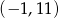 D)
D) 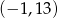
Do wykresu funkcji liniowej 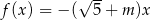 nie należy żaden punkt o obu współrzędnych dodatnich. Wynika stąd, że
nie należy żaden punkt o obu współrzędnych dodatnich. Wynika stąd, że
A) 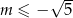 B)
B) 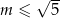 C)
C) 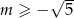 D)
D) 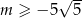
Punkty 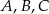 są punktami przecięcia paraboli o równaniu
są punktami przecięcia paraboli o równaniu 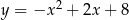 z osiami układu współrzędnych. Pole trójkąta
z osiami układu współrzędnych. Pole trójkąta 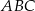 jest równe
jest równe
A) 8 B) 9 C) 24 D) 27
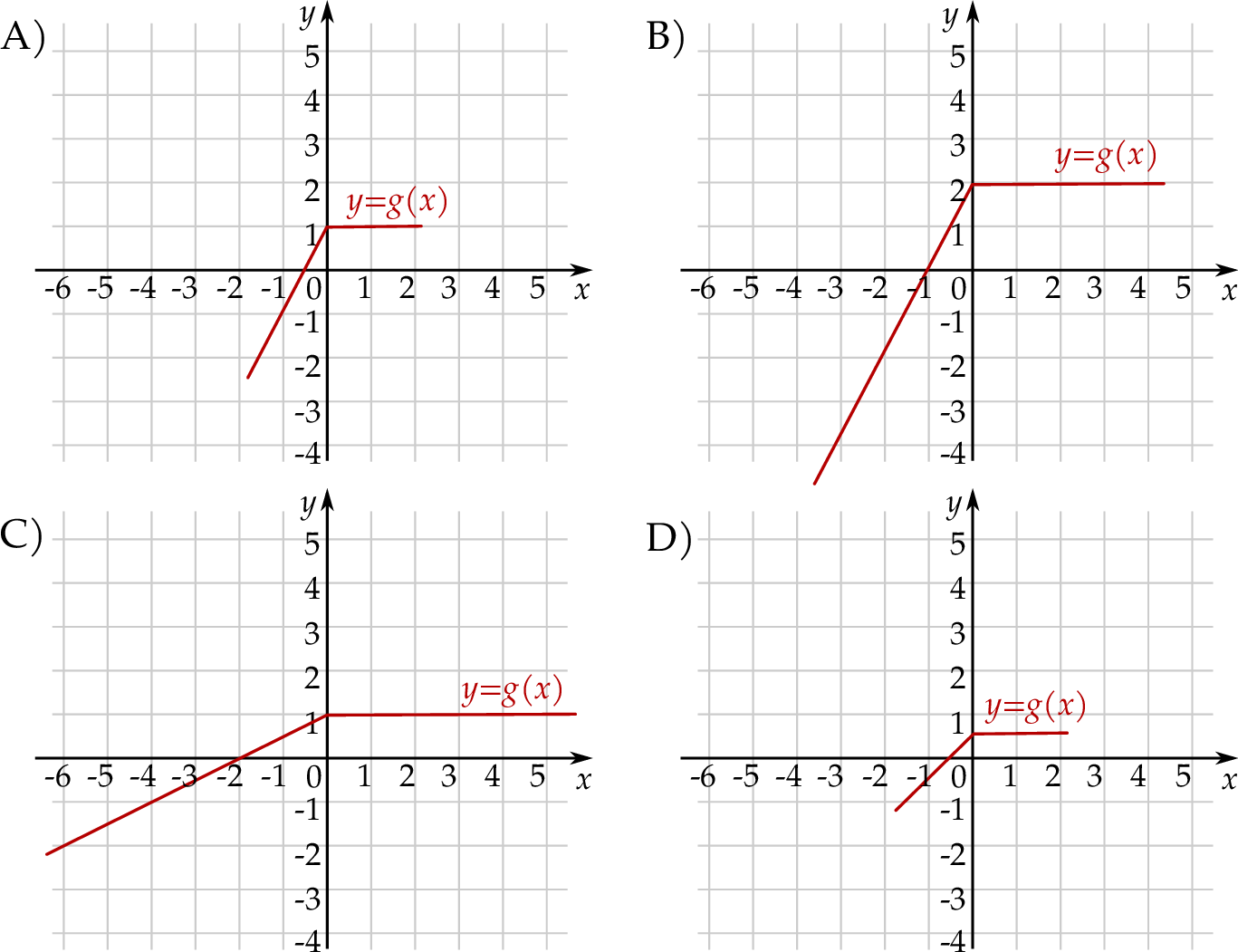
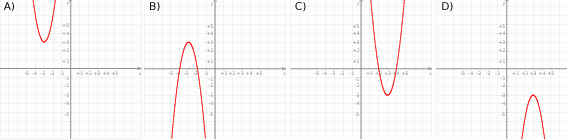
Funkcja 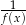 jest określona na całym zbiorze liczb rzeczywistych i nie przyjmuje wartości dodatnich. Na którym rysunku przedstawiono wykres funkcji
jest określona na całym zbiorze liczb rzeczywistych i nie przyjmuje wartości dodatnich. Na którym rysunku przedstawiono wykres funkcji 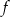 ?
?
Funkcja liniowa przyjmuje wartości dodatnie dla 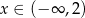 , a jej wykres przecina oś
, a jej wykres przecina oś 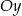 w punkcie
w punkcie 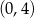 . Zatem jej wzór ma postać
. Zatem jej wzór ma postać
A) 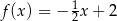 B)
B) 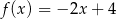 C)
C) 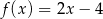 D)
D) 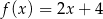
Punkt 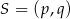 jest wierzchołkiem paraboli będącej wykresem funkcji
jest wierzchołkiem paraboli będącej wykresem funkcji 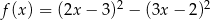 . Zatem
. Zatem
A) 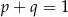 B)
B) 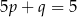 C)
C) 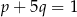 D)
D) 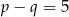
Ile punktów wspólnych z osią 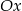 ma wykres funkcji kwadratowej
ma wykres funkcji kwadratowej 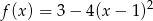 ?
?
A) 0 B) 1 C) 2 D) 3
Ile punktów wspólnych z osią 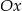 ma wykres funkcji kwadratowej
ma wykres funkcji kwadratowej 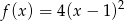 ?
?
A) 0 B) 1 C) 2 D) 3
Ile punktów wspólnych z osią 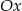 ma wykres funkcji kwadratowej
ma wykres funkcji kwadratowej 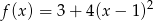 ?
?
A) 0 B) 1 C) 2 D) 3
Funkcja kwadratowa 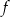 jest określona wzorem
jest określona wzorem 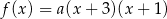 . Na rysunku przedstawiono fragment paraboli będącej wykresem tej funkcji. Jednym z punktów tej paraboli jest punkt
. Na rysunku przedstawiono fragment paraboli będącej wykresem tej funkcji. Jednym z punktów tej paraboli jest punkt 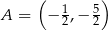 .
.
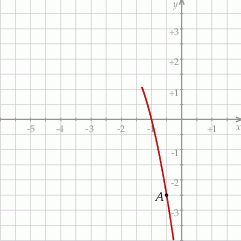
Najmniejsza wartość funkcji 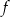 w przedziale
w przedziale 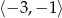 jest równa
jest równa
A) 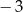 B) 0 C)
B) 0 C) 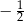 D)
D) 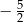
W kartezjańskim układzie współrzędnych  narysowano wykres funkcji
narysowano wykres funkcji 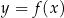 (zobacz rysunek).
(zobacz rysunek).
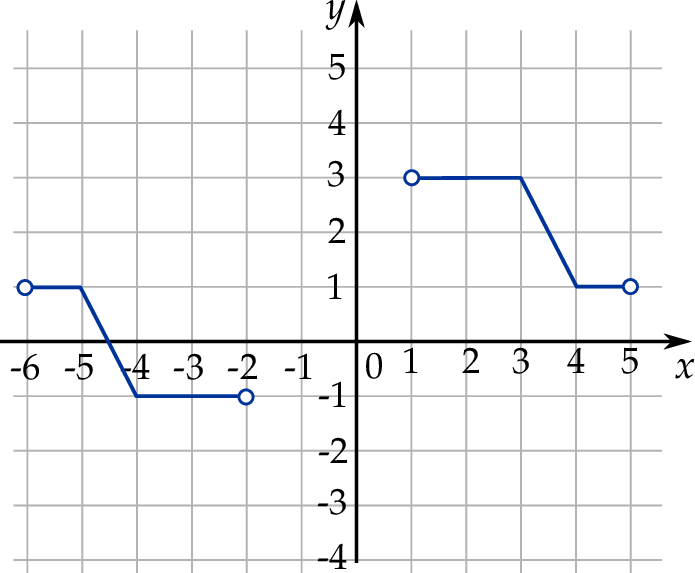
Zbiorem wartości funkcji 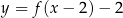 jest zbiór
jest zbiór
A) ![[− 3,1]](https://img.zadania.info/zad/6094235/HzadT4x.png) B)
B) ![[− 1 ,3 ]](https://img.zadania.info/zad/6094235/HzadT5x.png) C)
C) 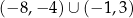
D) ![[− 5,− 1]∪ [1,5]](https://img.zadania.info/zad/6094235/HzadT7x.png) E)
E) ![[1,5]](https://img.zadania.info/zad/6094235/HzadT8x.png) F)
F) ![[− 5,− 3]](https://img.zadania.info/zad/6094235/HzadT9x.png)
Funkcja 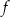 jest określona dla każdej liczby rzeczywistej
jest określona dla każdej liczby rzeczywistej  . Fragment wykresu funkcji
. Fragment wykresu funkcji 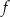 przedstawiono na poniższym rysunku.
przedstawiono na poniższym rysunku.
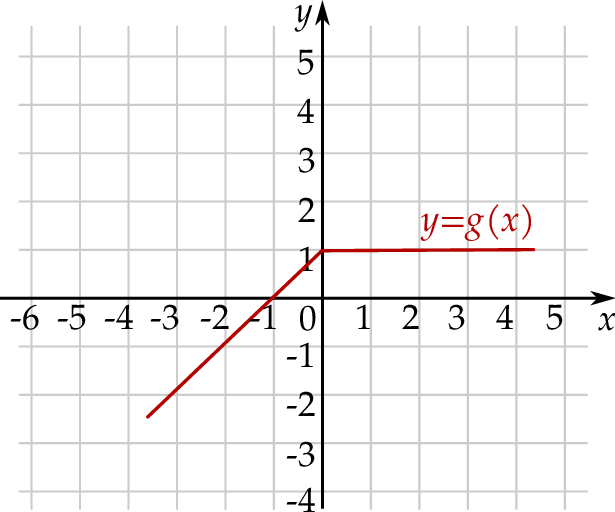
Funkcja 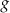 jest określona wzorem
jest określona wzorem 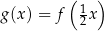 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Wskaż rysunek, na którym przedstawiony jest wykres funkcji
. Wskaż rysunek, na którym przedstawiony jest wykres funkcji 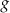 .
.