Dla której z podanych wartości  , wykres funkcji
, wykres funkcji 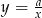 nie ma punktów wspólnych z wykresem funkcji
nie ma punktów wspólnych z wykresem funkcji 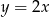 ?
?
A) 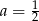 B)
B) 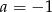 C)
C) 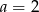 D)
D) 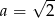
/Szkoła średnia/Zadania testowe/Funkcje - wykresy
Do wykresu funkcji 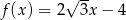 należy punkt o współrzędnych
należy punkt o współrzędnych
A) 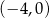 B)
B) 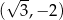 C)
C) 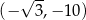 D)
D) 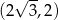
Wykres funkcji 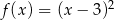 przesunięto równolegle o 2 jednostki w prawo. W wyniku tego przekształcenia otrzymano wykres funkcji
przesunięto równolegle o 2 jednostki w prawo. W wyniku tego przekształcenia otrzymano wykres funkcji
A) 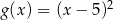 B)
B) 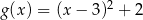 C)
C) 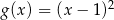 D)
D) 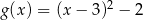
Punkt 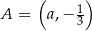 należy do wykresu funkcji liniowej
należy do wykresu funkcji liniowej 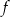 określonej wzorem
określonej wzorem 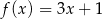 . Wynika stąd, że
. Wynika stąd, że
A) 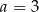 B)
B) 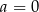 C)
C) 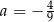 D)
D) 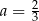
Wykres funkcji kwadratowej 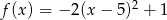 ma dwa punkty wspólne z prostą
ma dwa punkty wspólne z prostą
A) 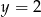 B)
B) 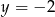 C)
C) 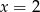 D)
D) 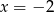
Rysunek przedstawia wykres funkcji 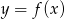 .
.
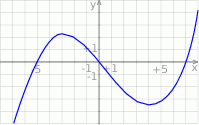
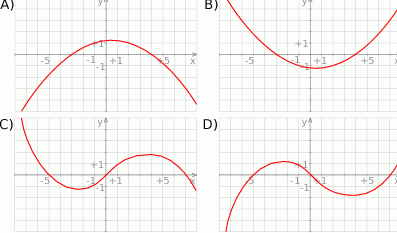
Wskaż wykres funkcji 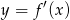 .
.
Rysunek przedstawia wykres funkcji 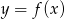 .
.
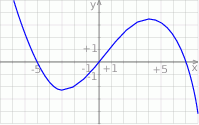
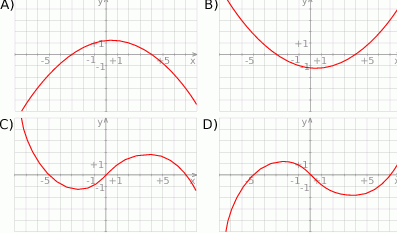
Wskaż wykres funkcji 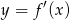 .
.
Miejscem zerowym funkcji liniowej 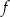 jest liczba 4048. Wykres tej funkcji przechodzi przez punkt
jest liczba 4048. Wykres tej funkcji przechodzi przez punkt 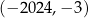 . Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Wykres funkcji 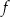 przecina oś przecina oś 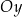 poniżej osi poniżej osi 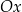 . . | P | F |
Liczba 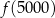 jest ujemna. jest ujemna. | P | F |
Dane są dwie funkcje określone dla wszystkich liczb rzeczywistych  wzorami
wzorami 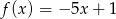 oraz
oraz 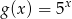 . Liczba punktów wspólnych wykresów tych funkcji jest równa
. Liczba punktów wspólnych wykresów tych funkcji jest równa
A) 3 B) 2 C) 1 D) 0
Dane są dwie funkcje określone dla wszystkich liczb rzeczywistych  wzorami
wzorami 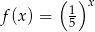 oraz
oraz 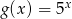 . Liczba punktów wspólnych wykresów tych funkcji jest równa
. Liczba punktów wspólnych wykresów tych funkcji jest równa
A) 0 B) 1 C) 2 D) 3
Dane są dwie funkcje określone dla wszystkich liczb rzeczywistych  wzorami
wzorami 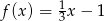 oraz
oraz 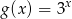 . Liczba punktów wspólnych wykresów tych funkcji jest równa
. Liczba punktów wspólnych wykresów tych funkcji jest równa
A) 3 B) 2 C) 1 D) 0
Wykres funkcji 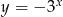 znajduje się w ćwiartkach
znajduje się w ćwiartkach
A) I i II B) II i III C) III i IV D) IV i I
Punkt 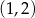 jest wierzchołkiem paraboli o równaniu
jest wierzchołkiem paraboli o równaniu
A) 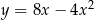 B)
B) 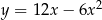 C)
C) 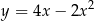 D)
D) 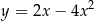
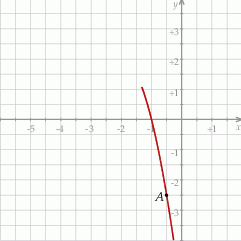
Funkcja kwadratowa 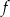 jest określona wzorem
jest określona wzorem 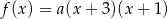 . Na rysunku przedstawiono fragment paraboli będącej wykresem tej funkcji. Jednym z punktów tej paraboli jest punkt
. Na rysunku przedstawiono fragment paraboli będącej wykresem tej funkcji. Jednym z punktów tej paraboli jest punkt 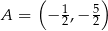 .
.
Osią symetrii paraboli będącej wykresem funkcji 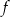 jest prosta o równaniu
jest prosta o równaniu
A) 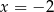 B)
B) 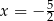 C)
C) 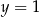 D)
D) 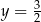
Do wykresu funkcji 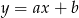 należą punkty
należą punkty 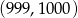 oraz
oraz 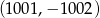 . Wówczas
. Wówczas
A) 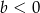 B)
B) 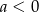 C)
C) 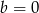 D)
D) 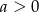
Do wykresu funkcji 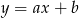 należą punkty
należą punkty 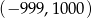 oraz
oraz 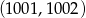 . Wówczas
. Wówczas
A) 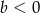 B)
B) 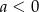 C)
C) 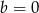 D)
D) 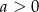
Do wykresu funkcji 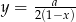 dla
dla 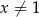 należy punkt
należy punkt 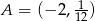 . Wtedy
. Wtedy
A) 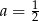 B)
B) 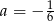 C)
C) 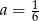 D)
D) 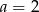
Funkcja kwadratowa 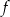 jest określona wzorem
jest określona wzorem 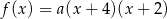 . Na rysunku przedstawiono fragment paraboli będącej wykresem tej funkcji. Jednym z punktów tej paraboli jest punkt
. Na rysunku przedstawiono fragment paraboli będącej wykresem tej funkcji. Jednym z punktów tej paraboli jest punkt 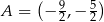 .
.
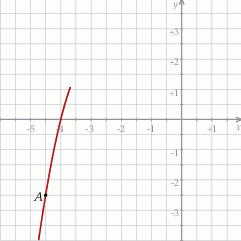
Najmniejsza wartość funkcji 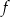 w przedziale
w przedziale 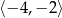 jest równa
jest równa
A) 0 B) 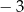 C)
C) 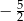 D)
D) 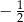
Do wykresu funkcji liniowej 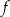 należy punkt
należy punkt 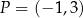 , a jej miejscem zerowym jest
, a jej miejscem zerowym jest 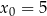 . Wzór funkcji
. Wzór funkcji 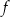 ma postać
ma postać
A) 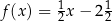 B)
B) 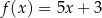 C)
C) 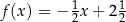 D)
D) 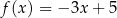
Miejscem zerowym funkcji liniowej 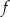 jest liczba 1. Wykres tej funkcji przechodzi przez punkt
jest liczba 1. Wykres tej funkcji przechodzi przez punkt 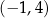 . Wzór funkcji
. Wzór funkcji 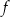 ma postać
ma postać
A) 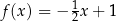 B)
B) 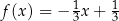
C) 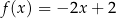 D)
D) 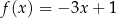
Miejscem zerowym funkcji liniowej 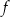 jest liczba
jest liczba 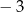 . Wykres tej funkcji przechodzi przez punkt
. Wykres tej funkcji przechodzi przez punkt 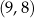 . Wzór funkcji
. Wzór funkcji 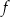 ma postać
ma postać
A) 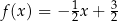 B)
B) 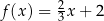
C) 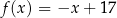 D)
D) 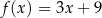
Dane są funkcje 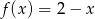 oraz
oraz 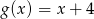 określone dla wszystkich liczb rzeczywistych
określone dla wszystkich liczb rzeczywistych  . Wskaż, który z poniższych wykresów jest wykresem funkcji
. Wskaż, który z poniższych wykresów jest wykresem funkcji 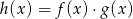 .
.
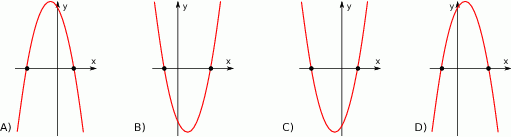
Dane są funkcje 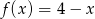 oraz
oraz 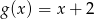 określone dla wszystkich liczb rzeczywistych
określone dla wszystkich liczb rzeczywistych  . Wskaż, który z poniższych wykresów jest wykresem funkcji
. Wskaż, który z poniższych wykresów jest wykresem funkcji 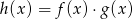 .
.
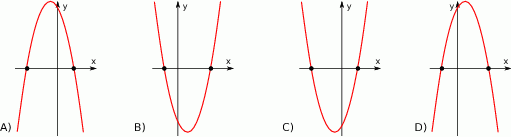
Wykresem funkcji kwadratowej 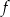 określonej wzorem
określonej wzorem 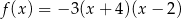 jest parabola o wierzchołku
jest parabola o wierzchołku 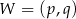 . Współrzędne wierzchołka
. Współrzędne wierzchołka 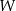 spełniają warunki
spełniają warunki
A) 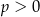 i
i 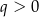 B)
B) 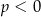 i
i 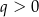 C)
C) 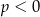 i
i 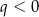 D)
D) 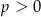 i
i 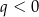
Wykresem funkcji kwadratowej 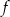 określonej wzorem
określonej wzorem 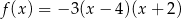 jest parabola o wierzchołku
jest parabola o wierzchołku 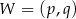 . Współrzędne wierzchołka
. Współrzędne wierzchołka 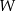 spełniają warunki
spełniają warunki
A) 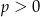 i
i 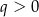 B)
B) 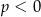 i
i 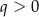 C)
C) 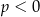 i
i 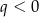 D)
D) 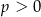 i
i 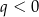
Wykres funkcji kwadratowej 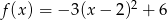 przecina oś
przecina oś 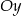 w punkcie o współrzędnych:
w punkcie o współrzędnych:
A) 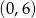 B)
B) 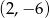 C)
C) 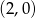 D)
D) 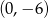
Wykres funkcji kwadratowej 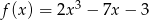 przecina oś
przecina oś 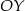 w punkcie
w punkcie
A) 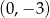 B)
B) 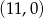 C)
C) 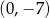 D)
D) 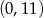
Wykres funkcji kwadratowej 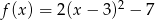 przecina oś
przecina oś 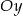 w punkcie
w punkcie
A) 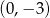 B)
B) 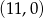 C)
C) 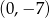 D)
D) 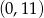
Prosta o równaniu 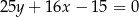 jest prostopadła do stycznej do wykresu funkcji
jest prostopadła do stycznej do wykresu funkcji 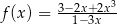 w punkcie
w punkcie
A) 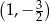 B)
B) 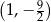 C)
C) 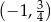 D)
D) 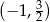
Na rysunku, w kartezjańskim układzie współrzędnych  , przedstawiono wykres funkcji
, przedstawiono wykres funkcji 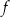 określonej dla każdego
określonej dla każdego 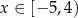 . Na tym wykresie zaznaczono punkty o współrzędnych całkowitych.
. Na tym wykresie zaznaczono punkty o współrzędnych całkowitych.
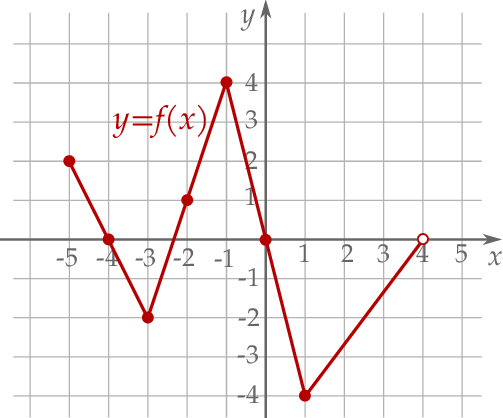
Najmniejsza wartość funkcji 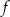 w przedziale
w przedziale ![[− 4,0]](https://img.zadania.info/zad/2389367/HzadT5x.png) jest równa
jest równa
A) 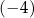 B)
B) 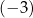 C)
C) 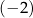 D) 0
D) 0

