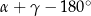Przekątna prostokąta ma długość 12 cm i tworzy z jednym z boków kąt o mierze 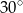 . Pole powierzchni tego prostokąta jest równe
. Pole powierzchni tego prostokąta jest równe
A) 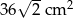 B)
B) 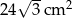 C)
C) 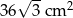 D)
D) 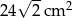
/Szkoła średnia/Zadania testowe/Geometria/Planimetria
Stosunek pól kół wpisanego i opisanego na kwadracie o boku długości  jest równy:
jest równy:
A) 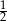 B)
B) 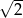 C)
C) 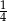 D)
D) 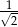
Stosunek pola kwadratu wpisanego w okrąg do pola kwadratu opisanego na tym okręgu wynosi
A) 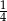 B)
B) 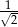 C)
C) 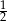 D)
D) 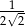
Stosunek pola koła wpisanego w kwadrat do pola koła opisanego na tym kwadracie jest równy:
A) 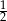 B)
B) 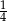 C)
C) 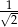 D)
D) 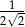
Sinus kąta ostrego równoległoboku jest równy  . Suma cosinusów wszystkich kątów wewnętrznych tego równoległoboku jest równa
. Suma cosinusów wszystkich kątów wewnętrznych tego równoległoboku jest równa
A) 0 B) 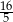 C)
C) 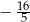 D)
D) 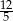
Przyprostokątne trójkąta prostokątnego mają długości 1 i 7. Sinus najmniejszego kąta tego trójkąta jest równy
A) 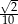 B)
B) 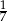 C)
C) 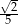 D)
D) 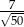
Przyprostokątne w trójkącie prostokątnym mają długości 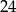 i
i 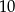 . Sinus najmniejszego kąta jest równy
. Sinus najmniejszego kąta jest równy
A) 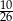 B)
B) 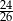 C)
C) 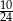 D)
D) 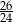
W trójkącie prostokątnym o długościach przyprostokątnych 2 i 5 cosinus większego z kątów ostrych jest równy
A)  B)
B)  C)
C) 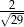 D)
D) 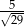
Przyprostokątne trójkąta prostokątnego mają długości 3 i 9. Sinus najmniejszego kąta tego trójkąta jest równy
A) 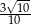 B)
B) 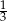 C)
C) 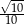 D)
D) 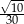
Przyprostokątne trójkąta prostokątnego mają długości 8 i 6. Sinus większego z kątów ostrych tego trójkąta jest równy
A)  B)
B)  C)
C)  D)
D) 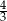
Przyprostokątne trójkąta prostokątnego mają długości 2 i 6. Sinus najmniejszego kąta tego trójkąta jest równy
A) 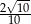 B)
B) 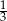 C)
C) 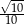 D)
D) 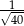
W trójkącie 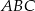 miary kątów wynoszą:
miary kątów wynoszą: 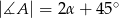 ,
, 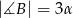 ,
, 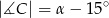 . Wówczas
. Wówczas
A) 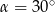 B)
B) 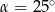 C)
C) 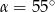 D)
D) 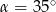
Stosunek długości podstawy do ramienia trójkąta równoramiennego jest równy 2:3. Ramię jest nachylone do podstawy pod kątem  , takim, że
, takim, że
A) 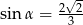 B)
B) 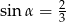 C)
C) 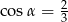 D)
D) 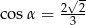
Stosunek długości podstawy do ramienia trójkąta równoramiennego jest równy 6:4. Ramię jest nachylone do podstawy pod kątem  , takim, że
, takim, że
A) 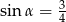 B)
B) 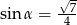 C)
C) 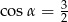 D)
D) 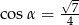
Stosunek długości podstawy do ramienia trójkąta równoramiennego jest równy 4:3. Ramię jest nachylone do podstawy pod kątem  , takim, że
, takim, że
A) 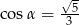 B)
B) 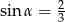 C)
C) 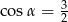 D)
D) 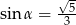
Dany jest trójkąt równoramienny 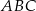 o kącie między ramionami
o kącie między ramionami 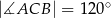 . Punkt
. Punkt 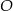 jest środkiem okręgu wpisanego w ten trójkąt. Prosta
jest środkiem okręgu wpisanego w ten trójkąt. Prosta 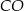 przecina podstawę
przecina podstawę 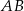 w punkcie
w punkcie 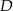 . Miara kąta
. Miara kąta 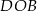 jest równa
jest równa
A) 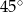 B)
B) 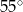 C)
C) 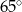 D)
D) 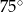
Dany jest trójkąt równoramienny 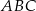 o kącie między ramionami
o kącie między ramionami 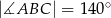 . Punkt
. Punkt 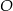 jest środkiem okręgu wpisanego w ten trójkąt. Prosta
jest środkiem okręgu wpisanego w ten trójkąt. Prosta 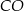 przecina podstawę
przecina podstawę 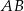 w punkcie
w punkcie 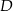 . Miara kąta
. Miara kąta 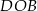 jest równa
jest równa
A) 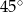 B)
B) 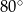 C)
C) 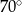 D)
D) 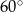
Dany jest trójkąt równoramienny 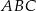 o kącie między ramionami
o kącie między ramionami 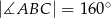 . Punkt
. Punkt 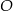 jest środkiem okręgu wpisanego w ten trójkąt. Prosta
jest środkiem okręgu wpisanego w ten trójkąt. Prosta 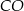 przecina podstawę
przecina podstawę 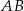 w punkcie
w punkcie 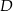 . Miara kąta
. Miara kąta 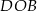 jest równa
jest równa
A) 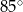 B)
B) 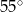 C)
C) 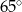 D)
D) 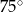
Trójkąty  i
i 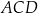 są wpisane w okrąg o środku
są wpisane w okrąg o środku 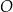 . Odcinek
. Odcinek 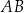 jest średnicą okręgu.
jest średnicą okręgu.

Miara kąta  zaznaczonego na rysunku jest równa
zaznaczonego na rysunku jest równa
A) 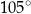 B)
B) 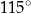 C)
C) 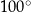 D)
D) 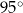
Trójkąty  i
i 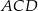 są wpisane w okrąg o środku
są wpisane w okrąg o środku 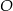 . Odcinek
. Odcinek 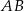 jest średnicą okręgu.
jest średnicą okręgu.
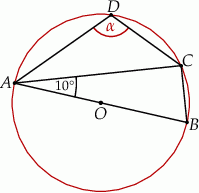
Miara kąta  zaznaczonego na rysunku jest równa
zaznaczonego na rysunku jest równa
A) 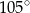 B)
B) 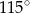 C)
C) 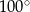 D)
D) 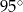
Trójkąty 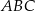 i
i 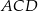 są wpisane w okrąg o środku
są wpisane w okrąg o środku 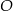 . Odcinek
. Odcinek 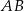 jest średnicą okręgu.
jest średnicą okręgu.
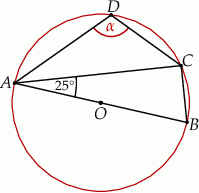
Miara kąta  zaznaczonego na rysunku jest równa
zaznaczonego na rysunku jest równa
A) 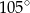 B)
B) 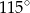 C)
C) 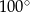 D)
D) 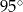
Długość jednego boku kwadratu 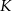 skrócono o 20%, a długość drugiego boku skrócono o 40%. W wyniku tych operacji otrzymano prostokąt
skrócono o 20%, a długość drugiego boku skrócono o 40%. W wyniku tych operacji otrzymano prostokąt 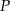 . Stosunek długości przekątnej kwadratu
. Stosunek długości przekątnej kwadratu 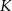 do długości przekątnej prostokąta
do długości przekątnej prostokąta 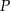 jest równy
jest równy
A) 0,48 B) 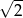 C) 1 D) 2
C) 1 D) 2
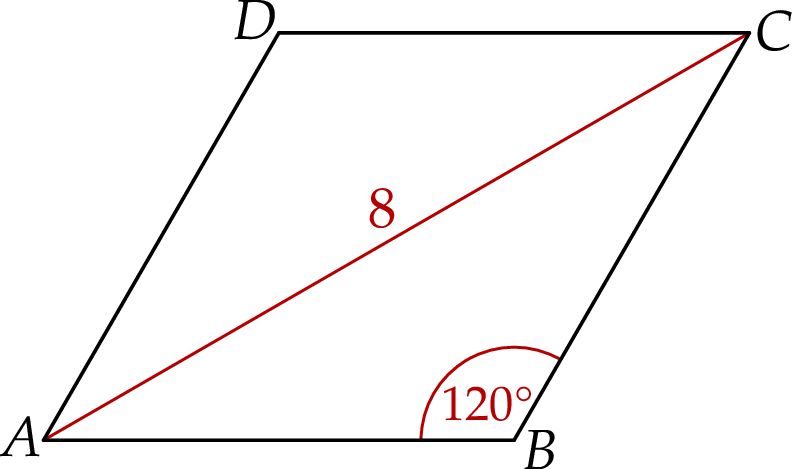
Przekątna 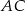 jest średnicą okręgu opisanego na czworokącie
jest średnicą okręgu opisanego na czworokącie 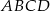 . Punkt przecięcia przekątnych dzieli przekątną
. Punkt przecięcia przekątnych dzieli przekątną 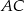 na odcinki o długościach 3 i 6. Zatem długość okręgu opisanego na czworokącie
na odcinki o długościach 3 i 6. Zatem długość okręgu opisanego na czworokącie 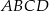 jest równa
jest równa
A) 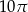 B)
B) 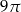 C)
C) 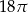 D)
D) 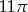
Dany jest romb o boku długości 4 i polu równym 8. Kąt rozwarty tego rombu ma miarę
A) 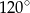 B)
B) 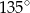 C)
C) 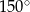 D)
D) 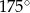
Pole trójkąta prostokątnego równoramiennego wynosi 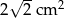 . Zatem przeciwprostokątna ma długość:
. Zatem przeciwprostokątna ma długość:
A) 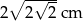 B)
B) 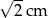 C)
C) 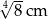 D)
D) 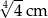
Pole trójkąta prostokątnego równoramiennego wynosi 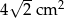 . Zatem przeciwprostokątna ma długość:
. Zatem przeciwprostokątna ma długość:
A) 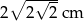 B)
B) 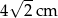 C)
C) 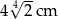 D)
D) 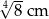
Pole trójkąta prostokątnego równoramiennego wynosi 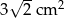 . Zatem przeciwprostokątna ma długość:
. Zatem przeciwprostokątna ma długość:
A) 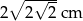 B)
B) 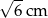 C)
C) 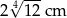 D)
D) 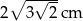
Pole trójkąta prostokątnego równoramiennego jest równe 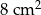 . Przeciwprostokątna tego trójkąta ma długość
. Przeciwprostokątna tego trójkąta ma długość
A) 8 cm B) 4 cm C) 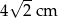 D)
D) 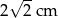
Przyprostokątna 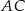 trójkąta prostokątnego
trójkąta prostokątnego 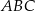 ma długość 6, a przeciwprostokątna
ma długość 6, a przeciwprostokątna 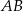 ma długość
ma długość 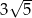 . Wtedy tangens kąta ostrego
. Wtedy tangens kąta ostrego 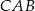 tego trójkąta jest równy
tego trójkąta jest równy
A) 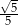 B)
B) 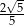 C)
C) 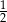 D) 2
D) 2
W trapezie 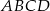 , w którym
, w którym 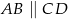 , przedłużono ramiona
, przedłużono ramiona 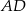 i
i 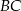 do przecięcia się w punkcie
do przecięcia się w punkcie 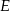 . Wiadomo, że
. Wiadomo, że 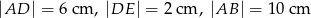 . Wobec tego odcinek
. Wobec tego odcinek 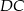 ma długość
ma długość
A) 2,5 cm B) 2 cm C) 3 cm D) 3,5 cm
W trapezie 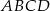 , w którym
, w którym 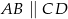 , przedłużono ramiona
, przedłużono ramiona 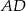 i
i 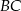 do przecięcia się w punkcie
do przecięcia się w punkcie 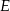 . Wiadomo, że
. Wiadomo, że 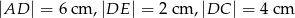 . Wobec tego odcinek
. Wobec tego odcinek 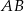 ma długość
ma długość
A) 15,5 cm B) 15 cm C) 16 cm D) 16,5 cm
W trapezie 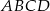 , w którym
, w którym 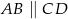 , przedłużono ramiona
, przedłużono ramiona 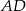 i
i 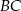 do przecięcia się w punkcie
do przecięcia się w punkcie 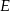 . Wiadomo, że
. Wiadomo, że 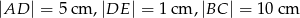 . Wobec tego odcinek
. Wobec tego odcinek 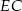 ma długość
ma długość
A) 2,5 cm B) 2 cm C) 3 cm D) 3,5 cm
Kąt  jest kątem ostrym w trójkącie prostokątnym i
jest kątem ostrym w trójkącie prostokątnym i 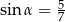 . Wówczas
. Wówczas
A) 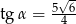 B)
B) 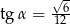 C)
C) 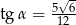 D)
D) 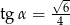
W rombie  dłuższa przekątna
dłuższa przekątna  ma długość 12 i tworzy z bokiem
ma długość 12 i tworzy z bokiem 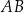 kąt o mierze
kąt o mierze 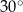 (zobacz rysunek).
(zobacz rysunek).
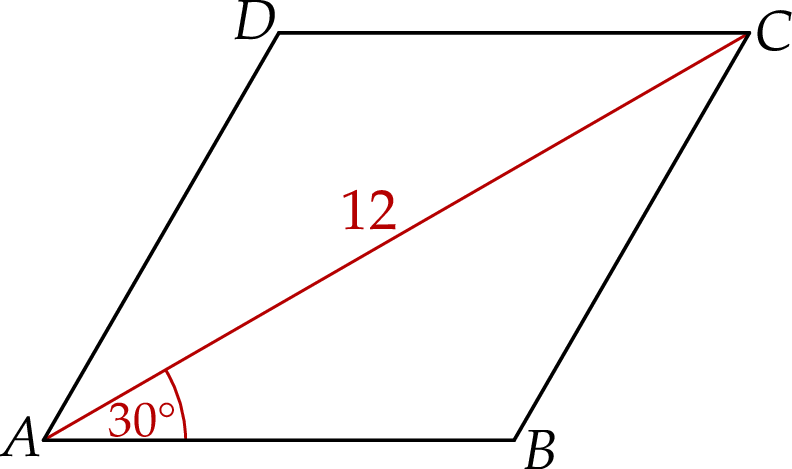
Pole rombu 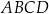 jest równe
jest równe
A) 24 B) 36 C) 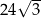 D)
D) 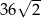
W rombie 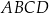 dłuższa przekątna
dłuższa przekątna 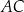 ma długość 8, a kąt rozwarty tego rombu ma miarę
ma długość 8, a kąt rozwarty tego rombu ma miarę 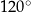 (zobacz rysunek).
(zobacz rysunek).
Pole rombu  jest równe
jest równe
A) 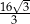 B) 8 C)
B) 8 C) 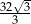 D) 16
D) 16
W trójkącie 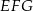 bok
bok 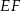 ma długość 21. Prosta równoległa do boku
ma długość 21. Prosta równoległa do boku 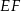 przecina boki
przecina boki 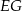 i
i 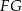 trójkąta odpowiednio w punktach
trójkąta odpowiednio w punktach 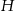 oraz
oraz 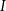 (zobacz rysunek) w taki sposób, że
(zobacz rysunek) w taki sposób, że 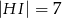 i
i 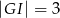 . Wtedy długość odcinka
. Wtedy długość odcinka 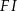 jest równa
jest równa
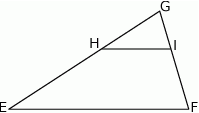
A) 6 B) 9 C) 12 D) 17
W trójkącie 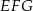 bok
bok 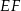 ma długość 24. Prosta równoległa do boku
ma długość 24. Prosta równoległa do boku 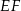 przecina boki
przecina boki 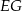 i
i 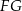 trójkąta odpowiednio w punktach
trójkąta odpowiednio w punktach 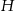 oraz
oraz 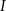 (zobacz rysunek) w taki sposób, że
(zobacz rysunek) w taki sposób, że 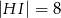 i
i 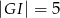 . Wtedy długość odcinka
. Wtedy długość odcinka 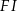 jest równa
jest równa
A) 6 B) 9 C) 10 D) 12
Przekątna prostokątna ma długość 6, a długość jego krótszego boku jest równa 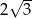 . Kąt rozwarty
. Kąt rozwarty  między przekątnymi tego prostokąta spełnia warunek
między przekątnymi tego prostokąta spełnia warunek
A) 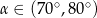 B)
B) 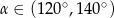 C)
C) 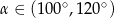 D)
D) 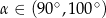
Ramię trójkąta równoramiennego 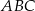 ma długość 8 cm i tworzy z podstawą kąt o mierze
ma długość 8 cm i tworzy z podstawą kąt o mierze 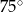 . Pole tego trójkąta jest równe
. Pole tego trójkąta jest równe
A) 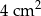 B)
B) 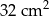 C)
C) 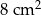 D)
D) 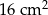
Dany jest trójkąt równoramienny, w którym ramię o długości 10 tworzy z podstawą kąt 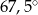 . Pole tego trójkąta jest równe
. Pole tego trójkąta jest równe
A) 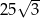 B)
B) 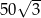 C)
C) 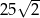 D)
D) 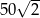
w trójkącie równoramiennym ramię ma długość 16 i tworzy z podstawą trójkąta kąt o mierze 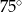 . Pole tego trójkąta jest równe
. Pole tego trójkąta jest równe
A) 128 B) 64 C) 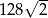 D)
D) 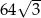
Dany jest trójkąt równoramienny, w którym ramię o długości 20 tworzy z podstawą kąt 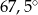 . Pole tego trójkąta jest równe
. Pole tego trójkąta jest równe
A) 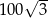 B)
B) 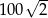 C)
C) 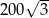 D)
D) 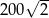
Punkty 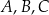 leżą na okręgu o środku
leżą na okręgu o środku 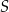 . Punkt
. Punkt 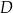 jest punktem przecięcia cięciwy
jest punktem przecięcia cięciwy 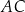 i średnicy okręgu poprowadzonej z punktu
i średnicy okręgu poprowadzonej z punktu 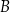 . Miara kąta
. Miara kąta 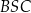 jest równa
jest równa  , a miara kąta
, a miara kąta 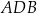 jest równa
jest równa 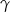 (zobacz rysunek).
(zobacz rysunek).

Wtedy kąt 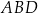 ma miarę
ma miarę
A) 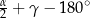 B)
B) 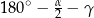 C)
C) 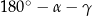 D)
D)