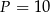Pole koła opisanego na trójkącie równobocznym o wysokości 9 jest równe
A) 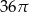 B)
B) 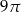 C)
C) 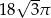 D)
D) 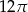
/Szkoła średnia/Zadania testowe/Geometria/Planimetria
Miara kąta wpisanego opartego na  okręgu wynosi:
okręgu wynosi:
A) 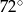 B)
B) 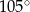 C)
C) 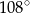 D)
D) 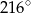
Miara kąta wpisanego opartego na łuku długości 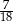 długości całego okręgu wynosi
długości całego okręgu wynosi
A) 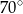 B)
B) 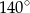 C)
C) 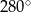 D)
D) 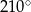
Kąt wpisany oparty jest na łuku, którego długość jest równa 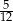 długości okręgu. Miara tego kąta wynosi
długości okręgu. Miara tego kąta wynosi
A) 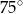 B)
B) 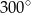 C)
C) 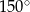 D)
D) 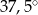
Jaką miarę ma kąt wpisany oparty na 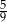 łuku okręgu?
łuku okręgu?
A) 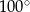 B)
B) 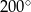 C)
C) 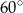 D)
D) 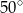
Miara kąta wpisanego opartego na  długości okręgu jest równa
długości okręgu jest równa
A) 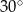 B)
B) 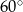 C)
C) 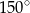 D)
D) 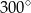
Dane są dwa okręgi: okrąg o środku w punkcie 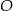 i promieniu 5 oraz okrąg o środku w punkcie
i promieniu 5 oraz okrąg o środku w punkcie 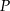 i promieniu 3. Odcinek
i promieniu 3. Odcinek 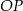 ma długość 16. Prosta
ma długość 16. Prosta 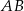 jest styczna do tych okręgów w punktach
jest styczna do tych okręgów w punktach 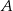 i
i 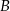 . Ponadto prosta
. Ponadto prosta 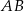 przecina odcinek
przecina odcinek 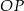 w punkcie
w punkcie  (zobacz rysunek).
(zobacz rysunek).
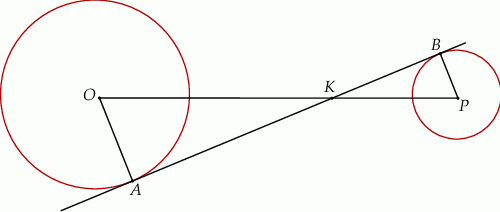
Wtedy
A) 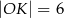 B)
B) 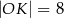 C)
C) 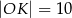 D)
D) 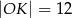
Dane są dwa okręgi: okrąg o środku w punkcie 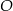 i promieniu 4 oraz okrąg o środku w punkcie
i promieniu 4 oraz okrąg o środku w punkcie 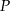 i promieniu 6. Odcinek
i promieniu 6. Odcinek 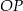 ma długość 25. Prosta
ma długość 25. Prosta 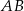 jest styczna do tych okręgów w punktach
jest styczna do tych okręgów w punktach 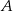 i
i 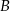 . Ponadto prosta
. Ponadto prosta 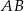 przecina odcinek
przecina odcinek 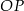 w punkcie
w punkcie 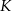 (zobacz rysunek).
(zobacz rysunek).
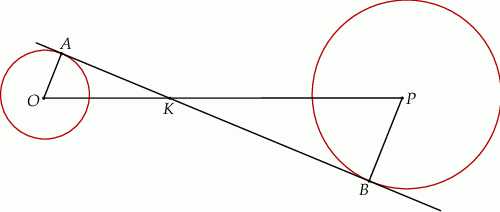
Wtedy
A) 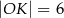 B)
B) 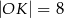 C)
C) 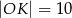 D)
D) 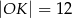
Końce odcinka 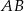 o długości 9 są środkami okręgów o promieniach 6 i 4 (zobacz rysunek).
o długości 9 są środkami okręgów o promieniach 6 i 4 (zobacz rysunek).
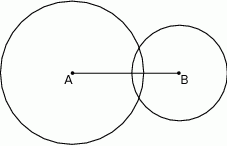
Punkt 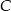 leży na odcinku
leży na odcinku 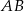 i jest środkiem takiego okręgu, o promieniu większym od 6, że dwa dane okręgi są do niego wewnętrznie styczne. Promień okręgu o środku
i jest środkiem takiego okręgu, o promieniu większym od 6, że dwa dane okręgi są do niego wewnętrznie styczne. Promień okręgu o środku 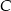 ma długość
ma długość
A) 6,5 B) 7,5 C) 8,5 D) 9,5
Jeżeli  jest kątem wewnętrznym trójkąta
jest kątem wewnętrznym trójkąta 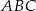 i
i 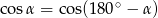 , to trójkąt
, to trójkąt 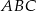 jest trójkątem
jest trójkątem
A) ostrokątnym B) prostokątnym C) rozwartokątnym D) równobocznym
Miara kąta  wynosi
wynosi
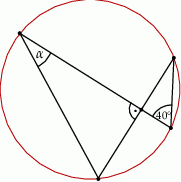
A) 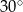 B)
B) 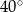 C)
C) 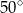 D)
D) 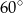
Punkty 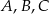 i
i 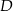 leżą na okręgu o środku w punkcie
leżą na okręgu o środku w punkcie 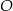 . Cięciwy
. Cięciwy 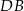 i
i 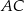 przecinają się w punkcie
przecinają się w punkcie 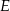 ,
, 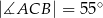 oraz
oraz 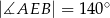 (zobacz rysunek).
(zobacz rysunek).
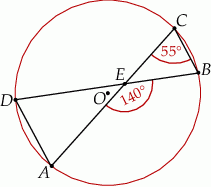
Miara kąta 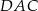 jest równa
jest równa
A) 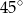 B)
B) 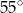 C)
C) 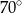 D)
D) 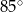
Miara kąta  wynosi
wynosi
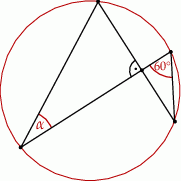
A) 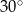 B)
B) 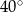 C)
C) 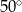 D)
D) 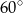
Miara kąta  wynosi
wynosi
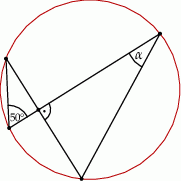
A) 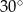 B)
B) 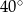 C)
C) 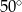 D)
D) 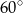
Kąt  na rysunku obok ma miarę
na rysunku obok ma miarę
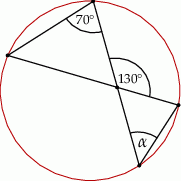
A) 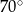 B)
B) 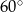 C)
C) 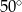 D)
D) 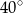
Punkty 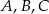 i
i 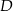 leżą na okręgu o środku w punkcie
leżą na okręgu o środku w punkcie 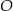 . Cięciwy
. Cięciwy 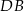 i
i 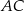 przecinają się w punkcie
przecinają się w punkcie 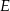 ,
, 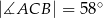 oraz
oraz 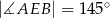 (zobacz rysunek).
(zobacz rysunek).
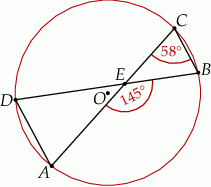
Miara kąta 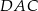 jest równa
jest równa
A) 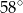 B)
B) 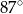 C)
C) 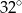 D)
D) 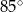
Pole trójkąta 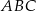 przedstawionego na rysunku jest równe
przedstawionego na rysunku jest równe
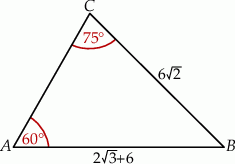
A) 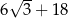 B)
B) 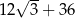 C)
C) 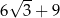 D)
D) 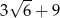
Dany jest kwadrat o przekątnej 6. Z wierzchołka kwadratu zatoczono koło o promieniu równym długości boku kwadratu. Pole figury będącej różnicą kwadratu i koła jest równe
A) 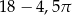 B)
B) 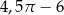 C)
C) 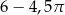 D)
D) 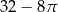
Dany jest kwadrat o przekątnej 2. Z wierzchołka kwadratu zatoczono koło o promieniu równym długości boku kwadratu. Pole figury będącej różnicą kwadratu i koła jest równe
A) 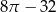 B)
B) 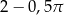 C)
C) 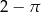 D)
D) 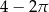
Dany jest kwadrat o przekątnej 4. Z wierzchołka kwadratu zatoczono koło o promieniu równym długości boku kwadratu. Pole figury będącej różnicą kwadratu i koła jest równe
A) 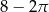 B)
B) 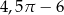 C)
C) 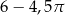 D)
D) 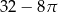
Pole trójkąta 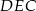 wynosi
wynosi 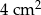 . Wiadomo, że
. Wiadomo, że 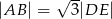 oraz
oraz 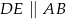 . Zatem pole trójkąta
. Zatem pole trójkąta 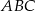 jest równe
jest równe
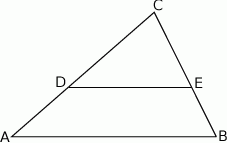
A) 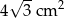 B)
B) 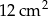 C)
C) 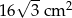 D)
D) 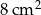
Stosunek boków prostokąta jest równy 1:2. Przekątna prostokąta tworzy z dłuższym bokiem prostokąta kąt  , taki, że
, taki, że
A) 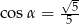 B)
B) 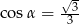 C)
C) 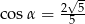 D)
D) 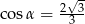
Stosunek boków prostokąta jest równy 2:3. Przekątna prostokąta tworzy z dłuższym bokiem prostokąta kąt  , taki, że
, taki, że
A) 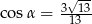 B)
B) 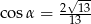 C)
C) 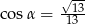 D)
D) 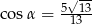
Stosunek boków prostokąta jest równy 1:2. Przekątna prostokąta tworzy z dłuższym bokiem prostokąta kąt  , taki, że
, taki, że
A) 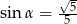 B)
B) 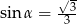 C)
C) 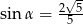 D)
D) 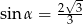
Stosunek boków prostokąta jest równy 2:3. Przekątna prostokąta tworzy z dłuższym bokiem prostokąta kąt  , taki, że
, taki, że
A) 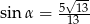 B)
B) 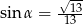 C)
C) 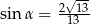 D)
D) 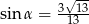
Stosunek boków prostokąta jest równy 1:3. Przekątna prostokąta tworzy z dłuższym bokiem prostokąta kąt  , taki, że
, taki, że
A) 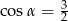 B)
B) 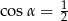 C)
C) 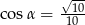 D)
D) 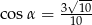
Punkty 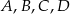 leżą na okręgu o środku
leżą na okręgu o środku 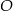 (zobacz rysunek). Miara zaznaczonego kąta
(zobacz rysunek). Miara zaznaczonego kąta  jest równa
jest równa
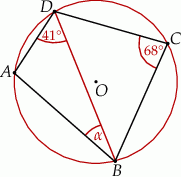
A) 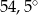 B)
B) 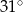 C)
C) 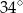 D)
D) 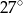
Punkty 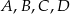 leżą na okręgu o środku
leżą na okręgu o środku 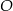 (zobacz rysunek). Miara zaznaczonego kąta
(zobacz rysunek). Miara zaznaczonego kąta  jest równa
jest równa
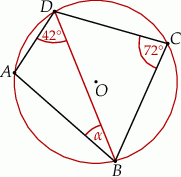
A) 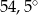 B)
B) 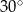 C)
C) 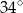 D)
D) 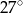
Punkty 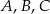 i
i 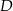 leżą na okręgu o środku
leżą na okręgu o środku 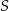 . Miary kątów
. Miary kątów 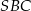 ,
, 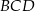 ,
, 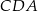 są równe odpowiednio:
są równe odpowiednio: 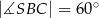 ,
, 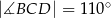 ,
, 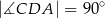 (zobacz rysunek).
(zobacz rysunek).
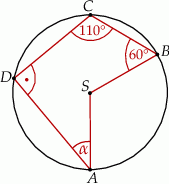
Wynika stąd, że miara  kąta
kąta 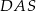 jest równa
jest równa
A) 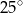 B)
B) 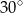 C)
C) 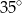 D)
D) 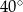
Punkty 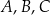 i
i 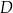 leżą na okręgu o środku
leżą na okręgu o środku 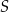 . Miary kątów
. Miary kątów 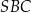 ,
, 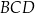 ,
, 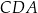 są równe odpowiednio:
są równe odpowiednio: 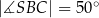 ,
, 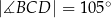 ,
, 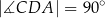 (zobacz rysunek).
(zobacz rysunek).
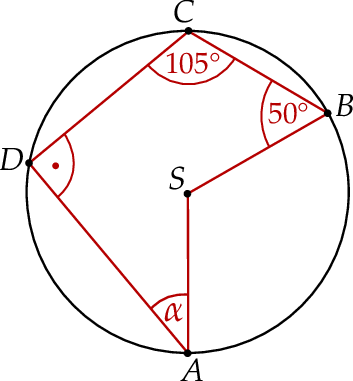
Wynika stąd, że miara  kąta
kąta 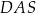 jest równa
jest równa
A) 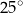 B)
B) 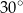 C)
C) 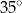 D)
D) 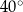
Punkty 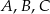 i
i 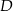 leżą na okręgu o środku
leżą na okręgu o środku 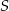 . Miary kątów
. Miary kątów 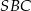 ,
, 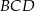 ,
, 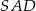 są równe odpowiednio:
są równe odpowiednio: 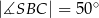 ,
, 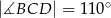 ,
, 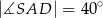 (zobacz rysunek).
(zobacz rysunek).
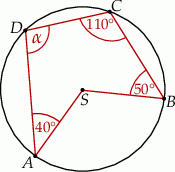
Wynika stąd, że miara  kąta
kąta 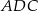 jest równa
jest równa
A) 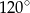 B)
B) 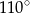 C)
C) 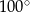 D)
D) 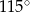
Trójkąt prostokątny ma boki długości 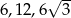 i kąty ostre
i kąty ostre 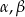 . Kąt
. Kąt 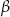 leży naprzeciw boku długości
leży naprzeciw boku długości 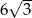 . Zatem
. Zatem
A) 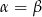 B)
B) 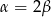 C)
C) 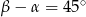 D)
D) 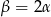
Trójkąt prostokątny ma boki długości 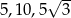 i kąty ostre
i kąty ostre 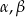 . Kąt
. Kąt 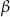 leży naprzeciw boku długości
leży naprzeciw boku długości 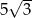 . Zatem
. Zatem
A) 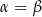 B)
B) 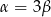 C)
C) 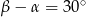 D)
D) 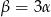
Trójkąt prostokątny ma boki długości 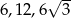 i kąty ostre
i kąty ostre 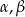 . Kąt
. Kąt 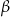 leży naprzeciw boku długości 6. Zatem
leży naprzeciw boku długości 6. Zatem
A) 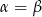 B)
B) 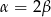 C)
C) 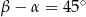 D)
D) 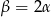
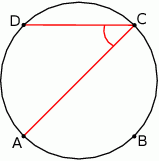
Punkty 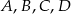 dzielą okrąg na 4 równe łuki. Miara zaznaczonego na rysunku kąta wpisanego
dzielą okrąg na 4 równe łuki. Miara zaznaczonego na rysunku kąta wpisanego 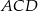 jest równa
jest równa
A) 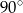 B)
B) 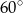 C)
C) 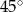 D)
D) 
Punkt 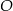 jest środkiem okręgu. Kąt środkowy
jest środkiem okręgu. Kąt środkowy 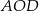 ma miarę
ma miarę
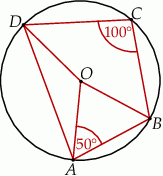
A) 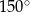 B)
B) 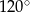 C)
C) 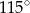 D)
D) 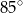
Punkty 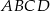 leżą na okręgu o środku
leżą na okręgu o środku 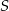 (zobacz rysunek). Miara kąta
(zobacz rysunek). Miara kąta 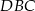 jest równa
jest równa
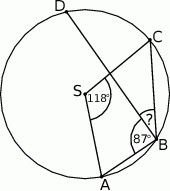
A) 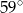 B)
B) 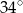 C)
C) 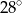 D)
D) 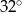
Punkt 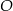 jest środkiem okręgu. Kąt środkowy
jest środkiem okręgu. Kąt środkowy 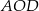 ma miarę
ma miarę
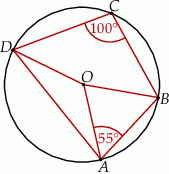
A) 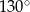 B)
B) 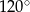 C)
C) 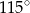 D)
D) 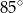
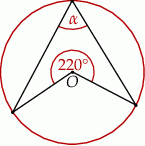
Punkt 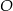 jest środkiem okręgu. Kąt wpisany
jest środkiem okręgu. Kąt wpisany  przedstawiony na rysunku ma miarę:
przedstawiony na rysunku ma miarę:
A) 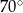 B)
B) 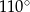 C)
C) 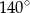 D)
D) 
Punkt 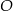 jest środkiem okręgu. Kąt wpisany
jest środkiem okręgu. Kąt wpisany  przedstawiony na rysunku ma miarę:
przedstawiony na rysunku ma miarę:
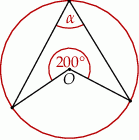
A) 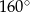 B)
B) 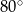 C)
C) 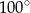 D)
D) 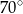
Miara kąta  (patrz rysunek obok) jest równa
(patrz rysunek obok) jest równa
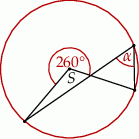
A) 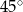 B)
B) 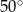 C)
C) 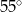 D)
D) 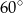
Środek 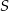 okręgu opisanego na trójkącie
okręgu opisanego na trójkącie 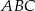 należy do boku
należy do boku 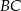 . Suma miar kątów
. Suma miar kątów 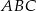 i
i 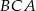 trójkąta
trójkąta 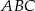 jest równa
jest równa
A) 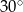 B)
B) 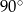 C)
C) 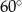 D)
D) 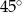
Środek 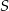 okręgu opisanego na trójkącie
okręgu opisanego na trójkącie 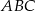 należy do boku
należy do boku 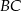 . Miara kąta
. Miara kąta 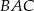 trójkąta
trójkąta 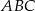 jest równa
jest równa
A) 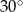 B)
B) 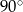 C)
C) 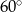 D)
D) 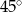
Na podstawie 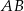 i ramieniu
i ramieniu 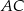 trójkąta równoramiennego
trójkąta równoramiennego 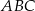 dane są punkty
dane są punkty 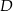 i
i 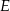 takie, że
takie, że 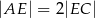 i
i 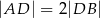 . Punkty
. Punkty 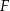 i
i 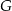 leżą na ramieniu
leżą na ramieniu 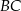 tak, że odcinki
tak, że odcinki 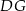 i
i 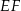 są prostopadłe do prostej
są prostopadłe do prostej 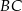 (zobacz rysunek).
(zobacz rysunek).
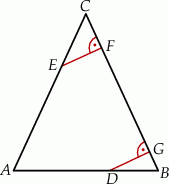
Pole trójkąta 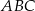 jest równe 18. Zatem suma pól trójkątów
jest równe 18. Zatem suma pól trójkątów 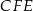 i
i 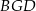 jest równa
jest równa
A) 9 B) 6 C) 3 D) 2
Punkty 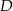 i
i 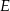 są środkami odpowiednio podstawy
są środkami odpowiednio podstawy 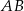 i ramienia
i ramienia 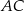 trójkąta równoramiennego
trójkąta równoramiennego 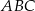 . Punkty
. Punkty 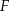 i
i 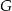 leżą na ramieniu
leżą na ramieniu 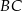 tak, że odcinki
tak, że odcinki 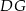 i
i 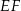 są prostopadłe do prostej
są prostopadłe do prostej 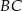 (zobacz rysunek).
(zobacz rysunek).
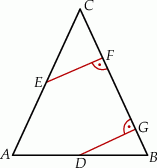
Pole trójkąta 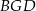 jest równe 2, a pole trójkąta
jest równe 2, a pole trójkąta 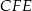 jest równe 4. Zatem pole trójkąta
jest równe 4. Zatem pole trójkąta 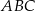 jest równe
jest równe
A) 24 B) 8 C) 12 D) 16
Kąt  w trójkącie prostokątnym przedstawionym na rysunku spełnia warunek
w trójkącie prostokątnym przedstawionym na rysunku spełnia warunek 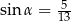 . Bok
. Bok 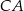 tego trójkąta ma długość:
tego trójkąta ma długość:
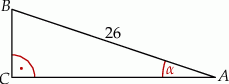
A) 10 B) 24 C) 12 D) 5
Dany jest trójkąt prostokątny o bokach długości 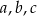 .
.
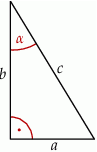
Jeżeli 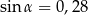 oraz
oraz 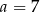 , to
, to
A) 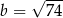 B)
B) 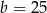 C)
C) 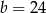 D)
D) 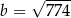
Kąt  w trójkącie prostokątnym przedstawionym na rysunku spełnia warunek
w trójkącie prostokątnym przedstawionym na rysunku spełnia warunek 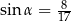 . Bok
. Bok 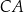 tego trójkąta ma długość:
tego trójkąta ma długość:
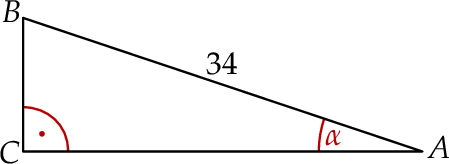
A) 30 B) 8 C) 16 D) 24
Jeśli 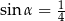 , to długość przyprostokątnej
, to długość przyprostokątnej 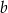 danego trójkąta (patrz rysunek) jest równa
danego trójkąta (patrz rysunek) jest równa
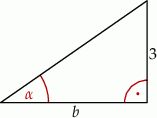
A) 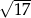 B)
B) 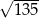 C)
C) 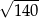 D)
D) 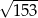
Jeśli 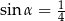 , to długość przyprostokątnej
, to długość przyprostokątnej  danego trójkąta (patrz rysunek) jest równa
danego trójkąta (patrz rysunek) jest równa
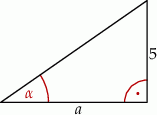
A) 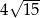 B)
B) 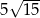 C)
C) 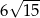 D)
D) 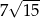
Miara kąta między bokiem 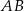 równoległoboku
równoległoboku 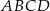 , a przekątną
, a przekątną 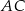 jest równa
jest równa 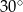 . Długość przekątnej
. Długość przekątnej 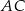 jest równa 5, a długość boku
jest równa 5, a długość boku 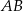 wynosi 4, zatem pole równoległoboku jest równe
wynosi 4, zatem pole równoległoboku jest równe
A) 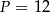 B)
B) 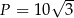 C)
C) 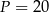 D)
D)