Kwadrat i trójkąt równoboczny mają równe pola. Stosunek długości boku kwadratu do długości boku trójkąta równobocznego jest wtedy równy
A) 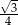 B)
B) 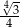 C)
C) 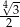 D)
D) 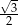
/Szkoła średnia/Zadania testowe/Geometria/Planimetria
Kwadrat i trójkąt równoboczny mają równe pola. Stosunek długości boku trójkąta równobocznego do długości boku kwadratu jest wtedy równy
A) 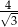 B)
B) 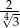 C)
C) 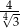 D)
D) 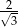
Długości boków trapezu równoramiennego są równe 12, 13, 2, 13.
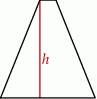
Wysokość 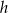 tego trapezu jest równa
tego trapezu jest równa
A) 5 B) 8 C) 10 D) 12
Długości boków trapezu równoramiennego są równe 19, 17, 3, 17.
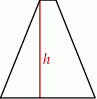
Wysokość 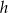 tego trapezu jest równa
tego trapezu jest równa
A) 16 B) 15 C) 14 D) 13
Trójkąt 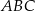 jest prostokątny. Odcinek
jest prostokątny. Odcinek 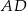 jest wysokością tego trójkąta poprowadzoną z wierzchołka
jest wysokością tego trójkąta poprowadzoną z wierzchołka 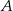 na przeciwprostokątną
na przeciwprostokątną 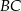 . Wtedy
. Wtedy
A) 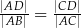 B)
B) 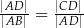 C)
C) 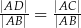 D)
D) 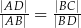
Kwadrat jest wpisany w okrąg o średnicy 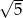 . Bok kwadratu jest równy
. Bok kwadratu jest równy
A) 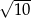 B)
B) 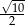 C)
C) 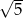 D)
D) 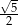
Okrąg opisany na kwadracie ma promień 4. Długość boku tego kwadratu jest równa
A) 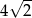 B)
B) 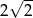 C) 8 D) 4
C) 8 D) 4
Kwadrat jest wpisany w okrąg o średnicy 4. Bok kwadratu jest równy
A) 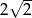 B)
B) 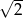 C)
C) 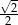 D)
D) 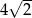
Okrąg opisany na kwadracie ma promień 6. Długość boku tego kwadratu jest równa
A) 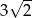 B)
B) 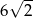 C) 12 D) 6
C) 12 D) 6
Kwadrat jest wpisany w okrąg o średnicy 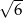 . Bok kwadratu jest równy
. Bok kwadratu jest równy
A) 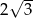 B)
B) 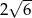 C)
C) 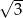 D) 3
D) 3
Okrąg opisany na kwadracie ma promień 8. Długość boku tego kwadratu jest równa
A) 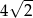 B)
B) 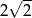 C)
C) 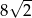 D) 8
D) 8
Odcinek 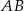 został podzielony punktami
został podzielony punktami 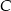 i
i 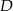 na takie trzy odcinki, że
na takie trzy odcinki, że 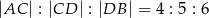 . Wybierz zdanie fałszywe
. Wybierz zdanie fałszywe
![]()
A) Odcinek 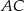 jest o 20% krótszy od odcinka
jest o 20% krótszy od odcinka 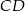
B) Długość odcinka 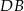 stanowi
stanowi  długości odcinka
długości odcinka 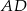
C) Długość odcinka 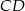 jest równa
jest równa 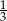 długości odcinka
długości odcinka 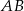
D) Odcinek 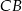 jest o 275% dłuższy od odcinek
jest o 275% dłuższy od odcinek 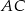
Odcinek  został podzielony punktami
został podzielony punktami  i
i  na takie trzy odcinki, że
na takie trzy odcinki, że 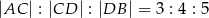 . Wybierz zdanie fałszywe
. Wybierz zdanie fałszywe
![]()
A) Odcinek 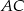 jest o 25% krótszy od odcinka
jest o 25% krótszy od odcinka 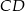
B) Długość odcinka  stanowi
stanowi  długości odcinka
długości odcinka 
C) Długość odcinka 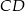 jest równa
jest równa 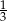 długości odcinka
długości odcinka 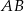
D) Odcinek 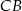 jest o 200% dłuższy od odcinka
jest o 200% dłuższy od odcinka 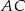
Odcinek 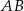 został podzielony punktami
został podzielony punktami 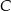 i
i 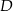 na takie trzy odcinki, że
na takie trzy odcinki, że 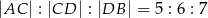 . Wybierz zdanie fałszywe
. Wybierz zdanie fałszywe
![]()
A) Odcinek 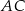 jest o 20% krótszy od odcinka
jest o 20% krótszy od odcinka 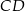
B) Długość odcinka 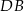 stanowi
stanowi 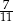 długości odcinka
długości odcinka 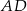
C) Długość odcinka 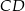 jest równa
jest równa 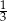 długości odcinka
długości odcinka 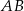
D) Odcinek 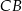 jest o 160% dłuższy od odcinka
jest o 160% dłuższy od odcinka 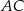
Okręgi o promieniach 3 i 4 są styczne zewnętrznie. Prosta styczna do okręgu o promieniu 4 w punkcie 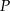 przechodzi przez środek okręgu o promieniu 3 (zobacz rysunek).
przechodzi przez środek okręgu o promieniu 3 (zobacz rysunek).
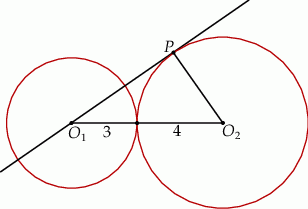
Pole trójkąta, którego wierzchołkami są środki okręgów i punkt styczności P, jest równe
A) 14 B) 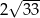 C)
C) 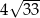 D) 12
D) 12
Okręgi o promieniach 3 i 4 są styczne zewnętrznie. Prosta styczna do okręgu o promieniu 3 w punkcie 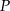 przechodzi przez środek okręgu o promieniu 4 (zobacz rysunek).
przechodzi przez środek okręgu o promieniu 4 (zobacz rysunek).
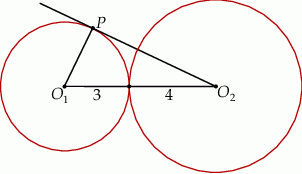
Pole trójkąta, którego wierzchołkami są środki okręgów i punkt styczności 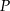 , jest równe
, jest równe
A) 21 B) 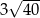 C)
C) 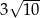 D) 24
D) 24
Okrąg opisany na sześciokącie foremnym ma promień 2. Promień okręgu wpisanego w ten sześciokąt jest równy
A) 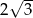 B)
B) 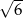 C)
C) 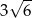 D)
D) 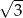
Okrąg opisany na sześciokącie foremnym ma promień 6. Promień okręgu wpisanego w ten sześciokąt jest równy
A) 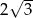 B)
B) 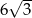 C)
C) 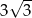 D)
D) 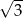
Większa część odcinka podzielonego na dwie części w stosunku 3:5 wynosi 20 cm. Długość tego odcinka wynosi:
A) 32 cm B) 27 cm C) 33 cm D) 30 cm
W kwadracie 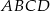 połączono środki boków otrzymując kwadrat
połączono środki boków otrzymując kwadrat 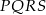 .
.
Kwadrat 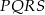 jest podobny do kwadratu
jest podobny do kwadratu 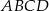 w skali
w skali
A) 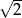 B) 2 C)
B) 2 C) 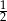 D)
D) 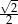
W kwadracie  połączono środki boków otrzymując kwadrat
połączono środki boków otrzymując kwadrat  .
.
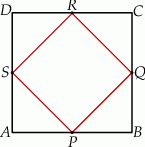
Kwadrat  jest podobny do kwadratu
jest podobny do kwadratu 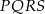 w skali
w skali
A) 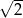 B) 2 C)
B) 2 C) 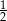 D)
D) 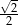
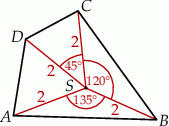
Na czworokącie 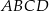 opisano okrąg o środku
opisano okrąg o środku 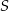 i promieniu
i promieniu 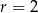 (zobacz rysunek). Pole tego czworokąta jest równe
(zobacz rysunek). Pole tego czworokąta jest równe
A) 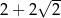 B) 4 C)
B) 4 C) 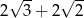 D)
D) 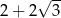
Dany jest trójkąt 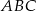 , w którym
, w którym 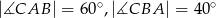 . Odcinki
. Odcinki 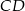 i
i 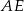 są dwusiecznymi kątów przy wierzchołkach
są dwusiecznymi kątów przy wierzchołkach 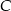 i
i 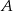 tego trójkąta. Zatem kąt
tego trójkąta. Zatem kąt  zaznaczony na rysunku ma miarę:
zaznaczony na rysunku ma miarę:
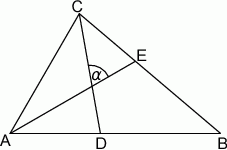
A) 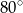 B)
B) 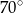 C)
C) 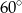 D)
D) 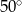
Dany jest trójkąt 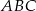 , w którym
, w którym 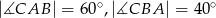 . Odcinki
. Odcinki 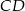 i
i 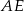 są dwusiecznymi kątów przy wierzchołkach
są dwusiecznymi kątów przy wierzchołkach 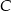 i
i 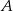 tego trójkąta. Zatem kąt
tego trójkąta. Zatem kąt  zaznaczony na rysunku ma miarę:
zaznaczony na rysunku ma miarę:
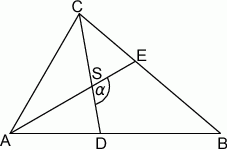
A) 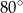 B)
B) 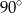 C)
C)  D)
D) 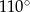
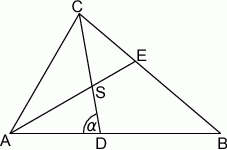
Dany jest trójkąt 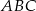 , w którym
, w którym 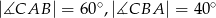 . Odcinki
. Odcinki 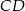 i
i 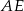 są dwusiecznymi kątów przy wierzchołkach
są dwusiecznymi kątów przy wierzchołkach 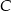 i
i 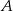 tego trójkąta. Zatem kąt
tego trójkąta. Zatem kąt  zaznaczony na rysunku ma miarę:
zaznaczony na rysunku ma miarę:
A) 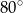 B)
B) 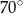 C)
C) 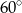 D)
D) 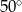
Odcinki 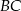 i
i 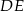 są równoległe. Długości odcinków
są równoległe. Długości odcinków 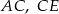 i
i 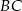 są podane na rysunku.
są podane na rysunku.
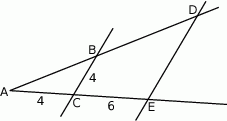
Długość odcinka 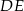 jest równa
jest równa
A) 6 B) 8 C) 10 D) 12
Odcinki 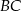 i
i 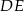 są równoległe. Długości odcinków
są równoległe. Długości odcinków 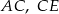 i
i 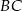 są podane na rysunku.
są podane na rysunku.
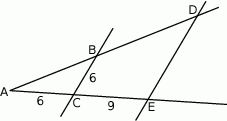
Długość odcinka 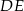 jest równa
jest równa
A) 18 B) 15 C) 12 D) 9
Długość okręgu wpisanego w trójkąt równoboczny wynosi 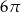 . Długość boku tego trójkąta jest równa
. Długość boku tego trójkąta jest równa
A) 9 B) 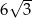 C)
C) 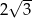 D) 6
D) 6
W trójkącie prostokątnym kąty ostre oznaczono  i
i 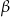 ,
, 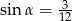 . Jaką miarę ma
. Jaką miarę ma 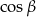 ?
?
A) 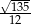 B)
B) 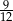 C)
C) 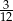 D)
D) 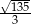
Na trójkącie równobocznym opisano koło, którego pole jest równe 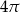 . Długość boku tego trójkąta jest równa
. Długość boku tego trójkąta jest równa
A) 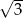 B)
B) 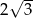 C)
C) 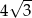 D) 3
D) 3
Na trójkącie równobocznym opisano koło, którego pole jest równe 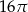 . Długość boku tego trójkąta jest równa
. Długość boku tego trójkąta jest równa
A) 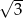 B)
B) 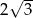 C)
C) 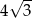 D) 3
D) 3
Pole koła opisanego na trójkącie równobocznym jest równe 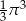 . Długość boku tego trójkąta jest równa
. Długość boku tego trójkąta jest równa
A) 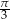 B)
B) 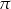 C)
C) 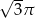 D)
D) 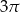
Na trójkącie równobocznym opisano koło, którego pole jest równe 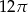 . Długość boku tego trójkąta jest równa
. Długość boku tego trójkąta jest równa
A) 6 B) 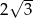 C)
C) 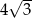 D) 3
D) 3
Pole koła wpisanego w trójkąt równoboczny jest równe 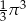 . Długość boku tego trójkąta jest równa
. Długość boku tego trójkąta jest równa
A) 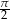 B)
B) 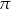 C)
C) 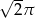 D)
D) 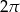
W trójkącie prostokątnym o przyprostokątnych długości 4 i 5 połączono wierzchołek 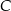 kąta prostego ze środkiem
kąta prostego ze środkiem 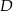 przeciwprostokątnej. Długość odcinka
przeciwprostokątnej. Długość odcinka 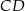 jest równa
jest równa
A) 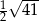 B) 4,5 C) 4 D)
B) 4,5 C) 4 D) 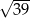
W trójkącie prostokątnym o przyprostokątnych długości 5 i 12 połączono wierzchołek 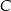 kąta prostego ze środkiem
kąta prostego ze środkiem 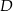 przeciwprostokątnej. Długość odcinka
przeciwprostokątnej. Długość odcinka  jest równa
jest równa
A) 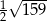 B) 6,5 C) 13 D)
B) 6,5 C) 13 D) 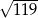
W trójkącie prostokątnym o przyprostokątnych długości 6 i 8 połączono wierzchołek 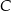 kąta prostego ze środkiem
kąta prostego ze środkiem 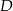 przeciwprostokątnej. Długość odcinka
przeciwprostokątnej. Długość odcinka 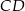 jest równa
jest równa
A)  B) 10 C) 7 D) 5
B) 10 C) 7 D) 5
W trójkącie prostokątnym o przyprostokątnych długości 7 i 24 połączono wierzchołek 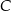 kąta prostego ze środkiem
kąta prostego ze środkiem 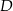 przeciwprostokątnej. Długość odcinka
przeciwprostokątnej. Długość odcinka 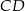 jest równa
jest równa
A) 25 B) 12 C) 15 D) 12,5
Długości boków trójkąta prostokątnego wynoszą 8 cm, 15 cm, 17 cm. Odcinek łączący środek przeciwprostokątnej z wierzchołkiem kąta prostego tego trójkąta ma długość
A) 8 cm B) 7,5 cm C) 9 cm D) 8,5 cm
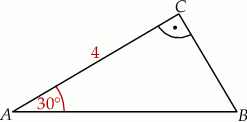
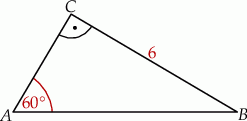
Pole trójkąta prostokątnego 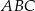 , przedstawionego na rysunku, jest równe
, przedstawionego na rysunku, jest równe
A) 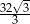 B)
B) 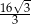 C)
C) 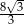 D)
D) 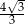
Pole trójkąta prostokątnego 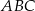 , przedstawionego na rysunku, jest równe
, przedstawionego na rysunku, jest równe
A) 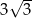 B)
B) 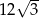 C)
C) 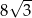 D)
D) 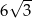
Na boku 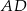 kwadratu
kwadratu 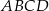 zbudowano trójkąt równoboczny
zbudowano trójkąt równoboczny 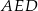 . Punkt
. Punkt 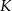 jest środkiem odcinka
jest środkiem odcinka 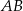 , a punkt
, a punkt 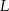 środkiem odcinka
środkiem odcinka 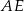 .
.
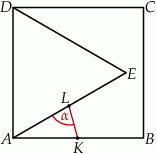
Miara kąta  jest równa
jest równa
A) 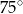 B)
B) 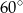 C)
C) 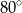 D)
D) 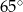
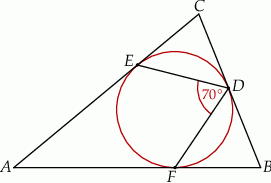
Punkty 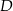 ,
, 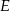 i
i 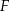 są punktami styczności okręgu wpisanego w trójkąt
są punktami styczności okręgu wpisanego w trójkąt 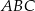 z jego bokami i
z jego bokami i 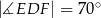 (zobacz rysunek).
(zobacz rysunek).
Miara kąta 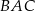 jest równa
jest równa
A) 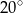 B)
B) 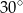 C)
C) 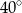 D)
D) 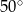
Odległość środka okręgu od prostej jest równa 0. Zatem liczba punktów wspólnych okręgu i prostej jest równa
A) 0 B) 1 C) 2 D) 3
Odległość środka okręgu o średnicy 14 od prostej jest równa 7. Zatem liczba punktów wspólnych okręgu i prostej jest równa:
A) 0 B) 1 C) 2 D) 3

