Zmieszano 100 litrów mleka 2% i 25 litrów mleka 4%. Otrzymano mleko, które ma w sobie 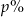 tłuszczu. Wynika stąd, że
tłuszczu. Wynika stąd, że
A) 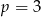 B)
B) 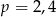 C)
C) 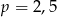 D)
D) 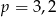
/Szkoła średnia/Zadania testowe/Zadania z treścią
Zmieszano 60 litrów mleka 2,5% i 40 litrów mleka 3%. Otrzymano mleko, które ma w sobie 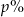 tłuszczu. Wynika stąd, że
tłuszczu. Wynika stąd, że
A) 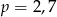 B)
B) 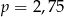 C)
C) 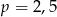 D)
D) 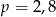
Zmieszano 15 g 20% roztworu z 25 g 12% roztworu. Stężenie procentowe otrzymanego roztworu jest równe
A) 15% B) 14% C) 16% D) 18%
Zmieszano 2,5 szklanki octu 6% z 1,5 szklanki octu 10%. Jakie jest stężenie otrzymanej mieszanki?
A) 9% B) 8% C) 7% D) 7,5%
Zmieszano 25 litrów mleka 2% i 100 litrów mleka 4%. Otrzymano mleko, które ma w sobie 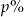 tłuszczu. Wynika stąd, że
tłuszczu. Wynika stąd, że
A) 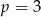 B)
B) 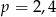 C)
C) 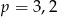 D)
D) 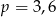
Metalowa podstawka ma mieć kształt prostokąta o obwodzie 140 cm i polu największym z możliwych. Podstawka powinna mieć zatem wymiary
A) 35 cm na 35 cm B) 20 cm na 50 cm C) 10 cm na 60 cm D) 55 cm na 15 cm
Piaskownica ma mieć kształt prostokąta o obwodzie 640 cm i polu największym z możliwych. Piaskownica powinna mieć zatem wymiary
A) 200 cm na 120 cm B) 160 cm na 160 cm C) 140 cm na 180 cm D) 320 cm na 320 cm
Metalowa podstawka ma mieć kształt prostokąta o obwodzie 120 cm i polu największym z możliwych. Podstawka powinna mieć zatem wymiary
A) 25 cm na 35 cm B) 20 cm na 40 cm C) 60 cm na 60 cm D) 30 cm na 30 cm
Stężenie roztworu kwasu siarkowego przez pierwszą godzinę pewnego eksperymentu było równe 25%. Na początku drugiej godziny eksperymentu stężenie zmalało o 5 punktów procentowych. Oznacza to, że stężenie tego roztworu kwasu siarkowego zmalało o
A) 5% B) 25% C) 20% D) 75%
Czas 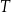 połowicznego rozpadu węgla
połowicznego rozpadu węgla 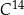 to czas, po którym względna zawartość tego izotopu w próbce materii organicznej zmniejsza się o połowę. Przyjmij, że czas połowicznego rozpadu węgla
to czas, po którym względna zawartość tego izotopu w próbce materii organicznej zmniejsza się o połowę. Przyjmij, że czas połowicznego rozpadu węgla 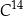 wynosi około
wynosi około 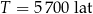 , a pozostała masa tego izotopu wyraża się wzorem
, a pozostała masa tego izotopu wyraża się wzorem
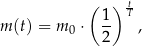
gdzie:
-
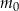 – masa izotopu węgla
– masa izotopu węgla 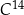 w trakcie życia organizmu
w trakcie życia organizmu -
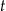 – czas jaki upłynął od czasu śmierci organizmu.
– czas jaki upłynął od czasu śmierci organizmu.
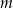 , to masa węgla
, to masa węgla 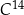 w tej próbce jest równa około
w tej próbce jest równa około A)
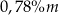 B)
B) 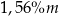 C)
C) 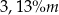 D)
D) 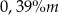
Na podstawie zasad dynamiki można udowodnić, że torem ruchu rzuconej piłki – przy pominięciu oporów powietrza – jest fragment paraboli. Koszykarz wykonał rzut do kosza z odległości 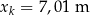 , licząc od środka piłki do środka obręczy kosza w linii poziomej. Do opisu toru ruchu przyjmiemy układ współrzędnych, w którym środek piłki w chwili początkowej znajdował się w punkcie
, licząc od środka piłki do środka obręczy kosza w linii poziomej. Do opisu toru ruchu przyjmiemy układ współrzędnych, w którym środek piłki w chwili początkowej znajdował się w punkcie 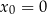 ,
, 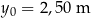 . Środek piłki podczas rzutu poruszał się po paraboli danej równaniem:
. Środek piłki podczas rzutu poruszał się po paraboli danej równaniem:
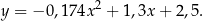
Rzut okazał się udany, a środek piłki przeszedł dokładnie przez środek kołowej obręczy kosza. Na rysunku poniżej przedstawiono tę sytuację oraz tor ruchu piłki w układzie współrzędnych.
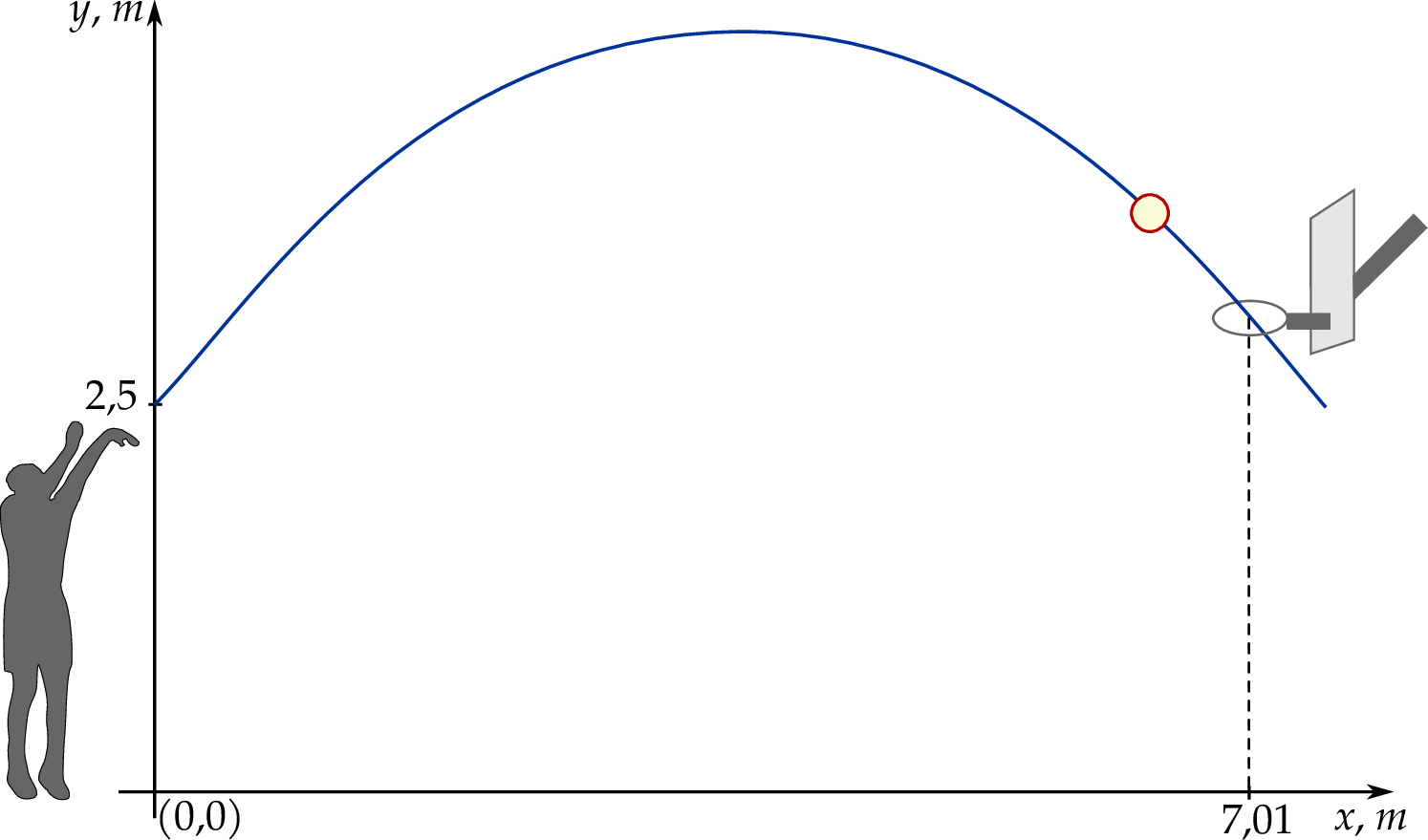
Obręcz kosza znajduje się na wysokości (podanej w zaokrągleniu z dokładnością do 0,01 m)
A) 3,04 m B) 3,06 m C) 3,80 m D) 4,93 m
Przekątna kartonu w kształcie sześcianu ma długość 3. Zatem przekątna podstawy tego kartonu ma długość
A) 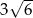 B)
B) 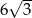 C)
C) 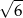 D)
D) 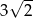
Przekątna pudełka w kształcie sześcianu ma długość 6. Zatem przekątna podstawy tego pudełka ma długość
A) 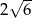 B)
B) 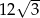 C)
C) 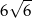 D)
D) 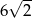
Przekątna doniczki w kształcie sześcianu ma długość 9. Zatem przekątna podstawy tego kartonu ma długość
A) 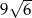 B)
B) 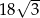 C)
C) 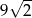 D)
D) 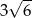
Klient wpłacił do banku 40 000 zł na lokatę trzyletnią. Po każdym rocznym okresie oszczędzania bank dolicza odsetki w wysokości 5% od kwoty bieżącego kapitału znajdującego się na lokacie. Po trzech latach oszczędzania od wartości odsetek doliczonych na tej lokacie pobrano podatek od zysków kapitałowych w wysokości 19%. Wartość pobranego podatku była równa
A) 6305 zł B) 1197,95 zł C) 23050 zł D) 4379,5 zł
W trakcie testów drogowych samochód numer 1 poruszał się ze stałą prędkością 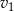 i pokonał trasę o 20% dłuższą, niż samochód nr 2, który poruszał się ze stałą prędkością
i pokonał trasę o 20% dłuższą, niż samochód nr 2, który poruszał się ze stałą prędkością 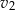 . Czas w jakim samochód nr 2 pokonał swoją trasę był o 25% krótszy, niż czas w jakim swoją trasę pokonał samochód nr 1. Stosunek prędkości
. Czas w jakim samochód nr 2 pokonał swoją trasę był o 25% krótszy, niż czas w jakim swoją trasę pokonał samochód nr 1. Stosunek prędkości 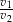 jest równy
jest równy
A) 1 B) 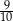 C)
C) 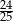 D)
D) 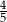
W trakcie testów drogowych samochód numer 1 poruszał się ze stałą prędkością 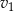 i pokonał trasę o 10% dłuższą, niż samochód nr 2, który poruszał się ze stałą prędkością
i pokonał trasę o 10% dłuższą, niż samochód nr 2, który poruszał się ze stałą prędkością 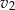 . Czas w jakim samochód nr 2 pokonał swoją trasę był o 20% krótszy, niż czas w jakim swoją trasę pokonał samochód nr 1. Stosunek prędkości
. Czas w jakim samochód nr 2 pokonał swoją trasę był o 20% krótszy, niż czas w jakim swoją trasę pokonał samochód nr 1. Stosunek prędkości 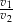 jest równy
jest równy
A) 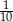 B)
B)  C)
C) 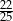 D)
D) 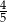
Suma pięciu kolejnych liczb całkowitych jest równa 195. Najmniejszą z tych liczb jest
A) 37 B) 38 C) 39 D) 40
Suma sześciu kolejnych liczb całkowitych jest równa 189. Najmniejszą z tych liczb jest
A) 32 B) 31 C) 30 D) 29
Piotrek ma 17 lat, a jego tata ma o 34 lata więcej. Wynika stąd, że tata ma od syna
A) 3 razy więcej lat B) 0 100% więcej lat C) 2 razy więcej lat D) o 50% więcej lat
Zenek ma 19 lat, a jego tata ma o 38 lat więcej. Wynika stąd, że tata ma od syna
A) o 300% więcej lat B) 0 100% więcej lat C) 2 razy więcej lat D) 3 razy więcej lat
Ewa ma 11 lat, a jej tata ma o 33 lata więcej. Wynika stąd, że tata ma od córki
A) 3 razy więcej lat B) 0 200% więcej lat C) 4 razy więcej lat D) o 100% więcej lat
Piłka rzucona z wysokości 48 m, odbijając się od ziemi, osiąga za każdym razem połowę poprzedniej wysokości. Jaką wysokość osiągnie po piątym odbiciu?
A) 2 m B) 3 m C) 1,5 m D) 75 cm
Piłka rzucona z wysokości 32 m, odbijając się od ziemi, osiąga za każdym razem połowę poprzedniej wysokości. Jaką wysokość osiągnie po siódmym odbiciu?
A) 2 m B) 1 m C) 50 cm D) 25 cm
Piłka rzucona z wysokości 32 m, odbijając się od ziemi, osiąga za każdym razem połowę poprzedniej wysokości. Jaką wysokość osiągnie po czwartym odbiciu?
A) 2 m B) 3 m C) 1,5 m D) 75 cm
Pionowy słupek o wysokości 90 cm rzuca cień o długości 60 cm. W tej samej chwili stojąca obok wieża rzuca cień długości 12 m. Jaka jest wysokość wieży?
A) 18 m B) 8 m C) 9 m D) 16 m
Pionowy słupek o wysokości 60 cm rzuca cień o długości 90 cm. W tej samej chwili stojąca obok wieża rzuca cień długości 12 m. Jaka jest wysokość wieży?
A) 18 m B) 8 m C) 9 m D) 16 m
Pan Grzegorz wpłacił do banku pewną kwotę na lokatę dwuletnią. Po każdym rocznym okresie oszczędzania bank doliczał odsetki w wysokości 5% od kwoty bieżącego kapitału znajdującego się na lokacie. Po dwóch latach oszczędzania pan Grzegorz odebrał z tego banku wraz z odsetkami kwotę 4851 zł (bez uwzględnienia podatków). Kwota wpłacona przez pana Grzegorza na tę lokatę była równa
A) 4300 zł B) 4400 zł C) 4500 zł D) 4600 zł
Pan Łukasz wpłacił do banku pewną kwotę na lokatę dwuletnią. Po każdym rocznym okresie oszczędzania bank doliczał odsetki w wysokości 5% od kwoty bieżącego kapitału znajdującego się na lokacie. Po dwóch latach oszczędzania pan Łukasz odebrał z tego banku wraz z odsetkami kwotę 5292 zł (bez uwzględnienia podatków). Kwota wpłacona przez pana Łukasza na tę lokatę była równa
A) 4800 zł B) 4400 zł C) 4500 zł D) 4600 zł
Na lokacie złożono 1000 zł przy rocznej stopie procentowej 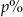 (procent składany). Odsetki naliczane są co kwartał. Po upływie roku wielkość kapitału na lokacie będzie równa
(procent składany). Odsetki naliczane są co kwartał. Po upływie roku wielkość kapitału na lokacie będzie równa
A) 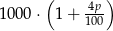 B)
B) 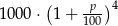 C)
C) 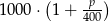 D)
D) 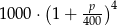
Na lokacie złożono 2000 zł przy rocznej stopie procentowej 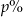 (procent składany). Odsetki naliczane są co pół roku. Po upływie dwóch lat wielkość kapitału na lokacie będzie równa
(procent składany). Odsetki naliczane są co pół roku. Po upływie dwóch lat wielkość kapitału na lokacie będzie równa
A) 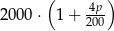 B)
B) 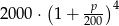 C)
C) 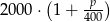 D)
D) 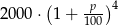
Zysk ze sprzedaży towaru w pewnej hurtowni w pierwszym miesiącu był równy 5000 zł, a w każdym następnym miesiącu o 5% wyższy w stosunku do miesiąca poprzedniego. Zysk hurtowni w szóstym miesiącu jej działalności opisuje wzór
A) 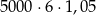 B)
B) 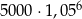 C)
C) 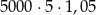 D)
D) 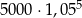
Klient wpłacił do banku na trzyletnią lokatę kwotę w wysokości 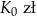 . Po każdym rocznym okresie oszczędzania bank dolicza odsetki w wysokości 6% od kwoty bieżącego kapitału znajdującego się na lokacie – zgodnie z procentem składanym. Po trzech latach oszczędzania w tym banku kwota na lokacie (bez uwzględniania podatków) jest równa
. Po każdym rocznym okresie oszczędzania bank dolicza odsetki w wysokości 6% od kwoty bieżącego kapitału znajdującego się na lokacie – zgodnie z procentem składanym. Po trzech latach oszczędzania w tym banku kwota na lokacie (bez uwzględniania podatków) jest równa
A) 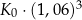 B)
B) 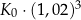 C)
C) 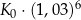 D)
D) 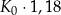
Proces stygnięcia naparu z ziół w otoczeniu o stałej temperaturze 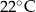 opisuje funkcja wykładnicza
opisuje funkcja wykładnicza 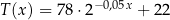 , gdzie
, gdzie 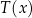 to temperatura naparu wyrażona w stopniach Celsjusza po
to temperatura naparu wyrażona w stopniach Celsjusza po  minutach liczonych od momentu
minutach liczonych od momentu 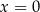 , w którym zioła zalano wrzątkiem. Temperatura naparu po 20 minutach od momentu zalania ziół wrzątkiem jest równa
, w którym zioła zalano wrzątkiem. Temperatura naparu po 20 minutach od momentu zalania ziół wrzątkiem jest równa
A) 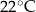 B)
B) 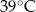 C)
C) 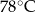 D)
D) 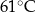
Proces stygnięcia herbaty w otoczeniu o stałej temperaturze 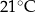 opisuje funkcja wykładnicza
opisuje funkcja wykładnicza 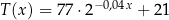 , gdzie
, gdzie 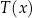 to temperatura herbaty wyrażona w stopniach Celsjusza po
to temperatura herbaty wyrażona w stopniach Celsjusza po  minutach liczonych od momentu
minutach liczonych od momentu 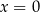 , w którym herbatę zalano wrzątkiem. Temperatura herbaty po 25 minutach od momentu zalania wrzątkiem jest równa
, w którym herbatę zalano wrzątkiem. Temperatura herbaty po 25 minutach od momentu zalania wrzątkiem jest równa
A) 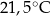 B)
B) 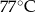 C)
C) 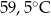 D)
D) 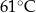
W pewnym obszarze leśnym początkowo rosło 10 000 trzydziestoletnich buków. Na tym obszarze rozpoczęto wyrąb tych drzew i przez 3 kolejne lata wycinano 10% pozostałych buków. Po 3 latach od rozpoczęcia wycinki liczba pozostałych buków jest równa
A) 7000 B) 8100 C) 6561 D) 7290
W grupie 100 osób 60 włada językiem angielskim, 50 – językiem niemieckim, 36 – językiem francuskim, 16 – angielskim i niemieckim, 19 – angielskim i francuskim, 15 – niemieckim i francuskim. Ile osób włada wszystkimi trzema wymienionymi językami?
A) 4 B) 16 C) 6 D) 20
W grupie 90 osób 60 włada językiem angielskim, 40 – językiem niemieckim, 32 – językiem francuskim, 21 – angielskim i niemieckim, 19 – angielskim i francuskim, 12 – niemieckim i francuskim. Ile osób włada wszystkimi trzema wymienionymi językami?
A) 4 B) 8 C) 6 D) 10
W solance, która zawierała 8% soli zwiększono zawartość soli o 187,5%. Stężenie soli w otrzymanym roztworze wynosi
A) 23% B) 20% C) 18% D) 25%
W solance, która zawierała 5% soli zwiększono zawartość soli o 500%. Stężenie soli w otrzymanym roztworze wynosi
A) 50% B) 30% C) 24% D) 25%

