Liczby  i
i  są dodatnie. Liczba
są dodatnie. Liczba 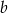 stanowi 48% liczby
stanowi 48% liczby  oraz 32% liczby
oraz 32% liczby  . Wynika stąd, że
. Wynika stąd, że
A) 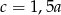 B)
B) 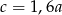 C)
C) 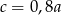 D)
D) 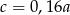
/Szkoła średnia/Zadania testowe/Liczby/Procenty
Liczba 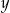 jest o 120% większa od dodatniej liczby
jest o 120% większa od dodatniej liczby  , a liczba
, a liczba  jest pięciokrotnie mniejsza od liczby
jest pięciokrotnie mniejsza od liczby 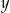 . Zatem
. Zatem
A) 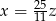 B)
B) 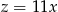 C)
C) 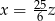 D)
D) 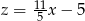
Liczby  i
i  są dodatnie. Liczba
są dodatnie. Liczba 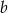 stanowi 42% liczby
stanowi 42% liczby  oraz 56% liczby
oraz 56% liczby  . Wynika stąd, że
. Wynika stąd, że
A) 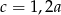 B)
B) 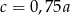 C)
C) 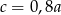 D)
D) 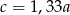
Liczba 120 jest o 50% większa od liczby  . Wynika stąd, że
. Wynika stąd, że
A) 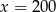 B)
B) 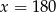 C)
C) 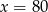 D)
D) 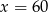
Liczba 180 jest o 50% większa od liczby  . Wynika stąd, że
. Wynika stąd, że
A) 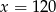 B)
B) 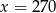 C)
C) 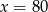 D)
D) 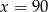
Liczba 90 jest o 50% większa od liczby  . Wynika stąd, że
. Wynika stąd, że
A) 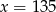 B)
B) 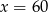 C)
C) 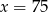 D)
D) 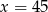
Jeżeli liczba 91 jest o 40% większa od liczby  , to liczba
, to liczba  jest równa
jest równa
A) 72 B) 70 C) 68 D) 65
30% liczby  jest o 2730 mniejsze od liczby
jest o 2730 mniejsze od liczby  . Liczba
. Liczba  jest równa
jest równa
A) 3900 B) 1911 C) 9100 D) 2100
Jeżeli liczba 78 jest o 50% większa od liczby  , to
, to
A) 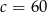 B)
B) 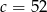 C)
C) 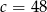 D)
D) 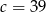
Liczba, która zwiększona o 15% będzie równa 437, to
A) 350 B) 368 C) 346,4 D) 380
Liczba, która zwiększona o 12% będzie równa 280, to
A) 250 B) 268 C) 246,4 D) 313,6
Liczba, która zwiększona o 15% będzie równa 414, to
A) 350 B) 360 C) 346,4 D) 313,6
Liczba 1371,37 jest o 37% większa od 44% połowy liczby  . Wtedy liczba
. Wtedy liczba  jest równa
jest równa
A) 9100 B) 2275 C) 4550 D) 5148
Liczba  jest o 20% większa od liczby
jest o 20% większa od liczby 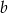 . Liczba
. Liczba 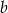 stanowi
stanowi
A) 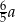 B)
B) 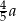 C)
C) 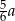 D) mniej niż 80% liczby
D) mniej niż 80% liczby 
Liczba  stanowi 80% liczby dodatniej
stanowi 80% liczby dodatniej 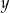 . Wynika stąd, że liczba
. Wynika stąd, że liczba 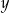 to
to
A) 125% liczby  B) 120% liczby
B) 120% liczby  C) 25% liczby
C) 25% liczby  D) 20% liczby
D) 20% liczby 
Liczba  jest o 40% większa od liczby
jest o 40% większa od liczby 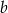 . Liczba
. Liczba 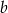 stanowi
stanowi
A) 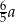 B)
B) 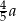 C)
C) 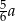 D) mniej niż 80% liczby
D) mniej niż 80% liczby 
Liczba  jest o 40% mniejsza od liczby
jest o 40% mniejsza od liczby 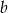 . Liczba
. Liczba 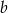 stanowi
stanowi
A) 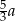 B)
B) 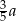 C)
C) 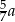 D) mniej niż 80% liczby
D) mniej niż 80% liczby 
Liczba  stanowi 125% liczby dodatniej
stanowi 125% liczby dodatniej 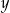 . Wynika stąd, że liczba
. Wynika stąd, że liczba 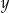 to
to
A) 125% liczby  B) 75% liczby
B) 75% liczby  C) 25% liczby
C) 25% liczby  D) 80% liczby
D) 80% liczby 
Liczba  stanowi 80% liczby dodatniej
stanowi 80% liczby dodatniej 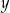 . Zatem 16% liczby
. Zatem 16% liczby 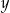 jest równe
jest równe
A) 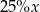 B)
B) 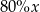 C)
C) 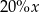 D)
D) 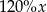
Gdy od 17% liczby 21 odejmiemy 21% liczby 17, to otrzymamy
A) 0 B) 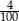 C) 3,57 D) 4
C) 3,57 D) 4
Gdy do 50% liczby 73 dodamy 73% liczby 50, to otrzymamy
A) 1 B) 73 C) 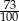 D) 100
D) 100
Gdy od 19% liczby 32 odejmiemy 16% liczby 19, to otrzymamy
A) 0 B) 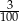 C) 3,04 D) 9,12
C) 3,04 D) 9,12
Połowę liczby  zwiększono o 20%. Otrzymano
zwiększono o 20%. Otrzymano
A) 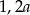 B)
B) 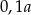 C)
C) 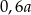 D)
D) 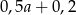
Połowę liczby  zmniejszono o 20%. Otrzymano
zmniejszono o 20%. Otrzymano
A) 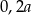 B)
B) 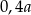 C)
C) 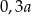 D)
D) 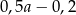
Jedną trzecią dodatniej liczby  zwiększono o 20%. Otrzymano w ten sposób
zwiększono o 20%. Otrzymano w ten sposób
A) 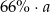 B)
B) 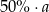 C)
C) 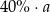 D)
D) 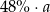
Ćwierć liczby  zwiększono o 40%. Otrzymano
zwiększono o 40%. Otrzymano
A) 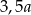 B)
B) 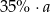 C)
C) 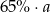 D)
D) 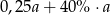
Połowę liczby  zwiększono o 40%. Otrzymano
zwiększono o 40%. Otrzymano
A) 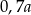 B)
B) 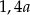 C)
C) 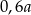 D)
D) 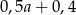
Jeżeli liczba 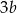 jest o 20% większa od połowy liczby
jest o 20% większa od połowy liczby 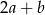 , to liczba
, to liczba  jest większa od
jest większa od 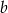 o
o
A) 100% B) 80% C) 50% D) 200%
Jeżeli liczba 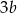 jest o 50% większa od połowy liczby
jest o 50% większa od połowy liczby 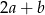 , to liczba
, to liczba  jest większa od
jest większa od 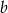 o
o
A) 100% B) 150% C) 50% D) 200%
Połowa liczby  jest o 25% mniejsza od trzeciej części liczby
jest o 25% mniejsza od trzeciej części liczby 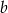 . Wtedy liczba
. Wtedy liczba 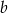 jest
jest
A) o 200% większa od 
B) o 100% większa od 
C) o 50% większa od 
D) o 150% większa od 
Liczba  to najmniejsza liczba pierwsza. Liczba
to najmniejsza liczba pierwsza. Liczba 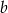 jest równa
jest równa 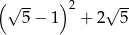 . Jakim procentem liczby
. Jakim procentem liczby  jest liczba
jest liczba 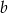 ?
?
A) 300% B) 600% C) 200% D) 400%
Liczba  to najmniejsza nieparzysta liczba pierwsza. Liczba
to najmniejsza nieparzysta liczba pierwsza. Liczba 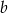 jest równa
jest równa 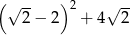 . Jakim procentem liczby
. Jakim procentem liczby  jest liczba
jest liczba 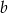 ?
?
A) 300% B) 600% C) 200% D) 400%
Liczba  to najmniejsza liczba pierwsza. Liczba
to najmniejsza liczba pierwsza. Liczba 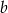 jest równa
jest równa 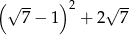 . Jakim procentem liczby
. Jakim procentem liczby  jest liczba
jest liczba 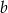 ?
?
A) 300% B) 600% C) 200% D) 400%
Liczby  i
i 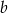 są dodatnie oraz 12% liczby
są dodatnie oraz 12% liczby  jest równe 15% liczby
jest równe 15% liczby 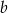 . Stąd wynika, że
. Stąd wynika, że  jest równe
jest równe
A) 103% liczby 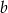 B) 125% liczby
B) 125% liczby 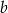 C) 150% liczby
C) 150% liczby 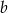 D) 153% liczby
D) 153% liczby 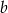
Liczby  i
i 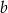 są dodatnie oraz 20% liczby
są dodatnie oraz 20% liczby  jest równe 25% liczby
jest równe 25% liczby 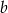 . Stąd wynika, że
. Stąd wynika, że  jest równe
jest równe
A) 125% liczby 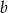 B) 120% liczby
B) 120% liczby 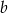 C) 115% liczby
C) 115% liczby  D) 110% liczby
D) 110% liczby 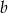
Liczby  i
i 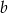 są dodatnie oraz 28% liczby
są dodatnie oraz 28% liczby  jest równe 49% liczby
jest równe 49% liczby 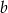 . Stąd wynika, że
. Stąd wynika, że  jest równe
jest równe
A) 57% liczby 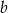 B) 125% liczby
B) 125% liczby 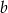 C) 175% liczby
C) 175% liczby 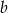 D) 149% liczby
D) 149% liczby 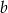
Liczby  i
i 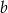 są dodatnie oraz 14% liczby
są dodatnie oraz 14% liczby  jest równe 21% liczby
jest równe 21% liczby 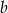 . Stąd wynika, że
. Stąd wynika, że  jest równe
jest równe
A) 103% liczby 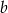 B) 125% liczby
B) 125% liczby 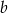 C) 150% liczby
C) 150% liczby 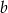 D) 153% liczby
D) 153% liczby 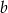
Dana jest liczba 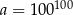 . Liczba
. Liczba 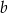 stanowi 1% liczby
stanowi 1% liczby  . Wówczas
. Wówczas
A) 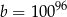 B)
B) 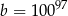 C)
C) 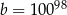 D)
D) 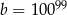
Suma liczby  i
i 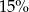 tej liczby jest równa 230. Równaniem opisującym tę zależność jest
tej liczby jest równa 230. Równaniem opisującym tę zależność jest
A) 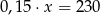 B)
B) 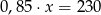 C)
C) 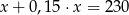 D)
D) 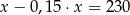
Różnica liczby  i
i 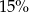 tej liczby jest równa 255. Równaniem opisującym tę zależność jest
tej liczby jest równa 255. Równaniem opisującym tę zależność jest
A) 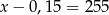 B)
B) 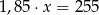 C)
C) 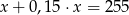 D)
D) 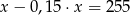
Liczba  stanowi 80% liczby dodatniej
stanowi 80% liczby dodatniej 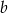 . O ile procent liczba
. O ile procent liczba 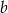 jest większa od liczby
jest większa od liczby  ?
?
A) 25% B) 80% C) 20% D) 120%
Liczba  stanowi 80% liczby dodatniej
stanowi 80% liczby dodatniej 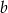 . Zatem liczba
. Zatem liczba 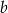 jest większa od liczby
jest większa od liczby  o:
o:
A) 15% B) 20% C) 25% D) 30%
Liczba  stanowi 125% liczby
stanowi 125% liczby 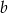 . O ile procent liczba
. O ile procent liczba 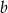 jest mniejsza od liczby
jest mniejsza od liczby  ?
?
A) 25% B) 80% C) 20% D) 120%
Liczba 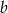 stanowi 40% liczby
stanowi 40% liczby  . O ile procent liczba
. O ile procent liczba  jest większa od liczby
jest większa od liczby 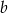 ?
?
A) 25% B) 60% C) 250% D) 150%
Jeżeli liczba  stanowi 40% dodatniej liczby
stanowi 40% dodatniej liczby 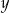 , to liczba
, to liczba 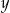 jest większa od liczby
jest większa od liczby  o:
o:
A) 60% B) 150% C) 160% D) 180%
Liczba 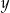 to 120% liczby
to 120% liczby  . Wynika stąd, że
. Wynika stąd, że
A) 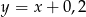 B)
B) 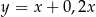 C)
C) 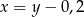 D)
D) 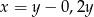
Liczba 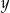 to 140% liczby
to 140% liczby  . Wynika stąd, że
. Wynika stąd, że
A) 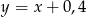 B)
B) 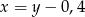 C)
C) 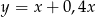 D)
D) 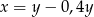
Liczba  stanowi 20% liczby
stanowi 20% liczby 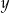 . Zatem prawdziwe jest następujące równanie
. Zatem prawdziwe jest następujące równanie
A) 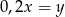 B)
B) 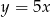 C)
C) 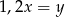 D)
D) 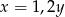
Dodatnia liczba  stanowi 30% liczby
stanowi 30% liczby 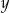 . Wówczas
. Wówczas
A) 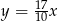 B)
B) 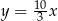 C)
C) 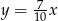 D)
D) 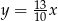
Liczba  jest o 30% większa od liczby
jest o 30% większa od liczby 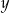 . Z tego wynika, że
. Z tego wynika, że
A) 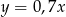 B)
B) 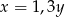 C)
C) 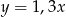 D)
D) 
Dodatnia liczba  stanowi 70% liczby
stanowi 70% liczby 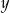 . Wówczas
. Wówczas
A) 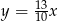 B)
B) 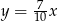 C)
C) 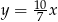 D)
D) 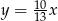
Liczba 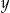 jest o 30% większa od liczby
jest o 30% większa od liczby  . Z tego wynika, że
. Z tego wynika, że
A) 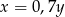 B)
B) 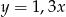 C)
C) 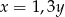 D)
D) 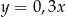
Liczba  stanowi 60% liczby
stanowi 60% liczby 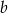 . Wówczas:
. Wówczas:
A) 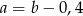 B)
B) 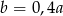 C)
C) 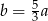 D)
D) 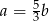
Liczba  jest o 30% mniejsza od liczby
jest o 30% mniejsza od liczby 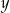 . Z tego wynika, że
. Z tego wynika, że
A) 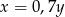 B)
B) 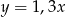 C)
C) 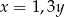 D)
D) 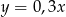
Wiadomo, że 8% pewnej liczby jest równe 10. Zatem 10% tej liczby wynosi
A) 12,5 B) 15 C) 18 D) 8
6% pewnej liczby jest równe 15. 14% tej liczby jest równe
A) 28 B) 36 C) 32 D) 35
Jeśli, 120% pewnej liczby jest równe 480, to 75% tej liczby jest równe
A) 250 B) 300 C) 350 D) 400
Wiadomo, że 9% pewnej liczby jest równe 16,2. Zatem 10% tej liczby wynosi
A) 12,5 B) 15 C) 18 D) 8
Wiadomo, że 8% pewnej liczby jest równe 10. Zatem 12% tej liczby wynosi
A) 12,5 B) 15 C) 18 D) 8
Liczby  i
i  są dodatnie. Liczba
są dodatnie. Liczba 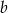 stanowi 96% liczby
stanowi 96% liczby 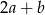 oraz 64% liczby
oraz 64% liczby 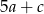 . Wynika stąd, że
. Wynika stąd, że
A) 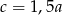 B)
B) 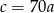 C)
C) 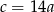 D)
D) 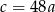
Liczby  i
i  są dodatnie. Liczba
są dodatnie. Liczba 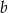 stanowi 96% liczby
stanowi 96% liczby 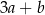 oraz 120% liczby
oraz 120% liczby 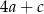 . Wynika stąd, że
. Wynika stąd, że
A) 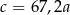 B)
B) 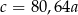 C)
C) 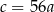 D)
D) 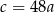
Liczba 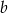 to 125% liczby
to 125% liczby  . Wskaż zdanie fałszywe.
. Wskaż zdanie fałszywe.
A) 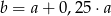 B)
B) 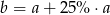 C)
C) 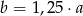 D)
D) 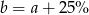
Liczba 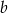 to 95% liczby
to 95% liczby  . Wskaż zdanie fałszywe.
. Wskaż zdanie fałszywe.
A) 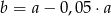 B)
B) 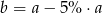 C)
C) 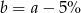 D)
D) 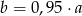
Liczba 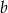 jest 3 razy większa od liczby
jest 3 razy większa od liczby  . Wtedy
. Wtedy
A) 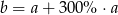 B)
B) 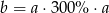 C)
C) 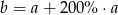 D)
D) 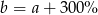
Liczba 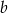 jest 2 razy większa od liczby
jest 2 razy większa od liczby  . Wtedy
. Wtedy
A) 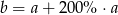 B)
B) 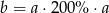 C)
C) 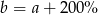 D)
D) 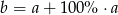
Liczba, której 4% jest równe 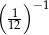 , to
, to
A) 300 B) 100 C) 0,12 D) 0,48
Liczba, której 5% jest równe 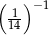 , to
, to
A) 210 B) 70 C) 0,14 D) 280
Liczba, której 8% jest równe 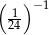 , to
, to
A) 100 B) 300 C) 0,12 D) 0,48
Iloczyn dodatnich liczb 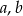 i
i  jest równy 6048. Ponadto 9% liczby
jest równy 6048. Ponadto 9% liczby  jest równe 8% liczby
jest równe 8% liczby 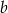 , oraz 70% liczby
, oraz 70% liczby 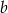 jest równe 60% liczby
jest równe 60% liczby  . Stąd wynika, że iloczyn
. Stąd wynika, że iloczyn 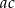 jest równy
jest równy
A) 288 B) 378 C) 324 D) 336

