Dwusieczne czworokąta 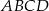 wpisanego w okrąg przecinają się w czterech różnych punktach:
wpisanego w okrąg przecinają się w czterech różnych punktach: 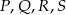 (zobacz rysunek).
(zobacz rysunek).
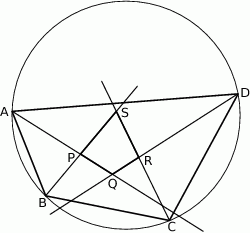
Wykaż, że na czworokącie 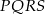 można opisać okrąg.
można opisać okrąg.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Dwusieczne czworokąta 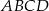 wpisanego w okrąg przecinają się w czterech różnych punktach:
wpisanego w okrąg przecinają się w czterech różnych punktach: 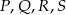 (zobacz rysunek).
(zobacz rysunek).

Wykaż, że na czworokącie 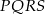 można opisać okrąg.
można opisać okrąg.
Ciąg 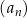 jest określony wzorem
jest określony wzorem 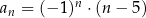 dla każdej liczby naturalnej
dla każdej liczby naturalnej 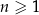 . Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Pierwszy wyraz ciągu 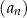 jest dwa razy większy od trzeciego wyrazu tego ciągu. jest dwa razy większy od trzeciego wyrazu tego ciągu. | P | F |
Wszystkie wyrazy ciągu 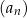 są dodatnie. są dodatnie. | P | F |
Ciąg 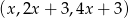 jest geometryczny. Pierwszy wyraz tego ciągu jest równy
jest geometryczny. Pierwszy wyraz tego ciągu jest równy
A) 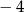 B) 1 C) 0 D)
B) 1 C) 0 D) 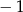
Dany jest ostrosłup, którego podstawą jest kwadrat o boku 6. Jedna z krawędzi bocznych tego ostrosłupa ma długość 12 i jest prostopadła do płaszczyzny podstawy. Oblicz objętość tego ostrosłupa.
Jednym z miejsc zerowych funkcji kwadratowej 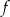 jest liczba
jest liczba 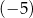 . Pierwsza współrzędna wierzchołka paraboli, będącej wykresem funkcji
. Pierwsza współrzędna wierzchołka paraboli, będącej wykresem funkcji 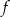 , jest równa 3. Drugim miejscem zerowym funkcji
, jest równa 3. Drugim miejscem zerowym funkcji 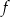 jest liczba
jest liczba
A) 11 B) 1 C) 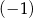 D)
D) 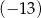
Zbiorem wszystkich rozwiązań nierówności 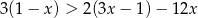 jest przedział
jest przedział
A) 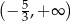 B)
B) 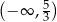 C)
C) 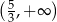 D)
D) 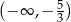
Na rysunku przedstawiono geometryczną interpretację jednego z niżej zapisanych układów równań.
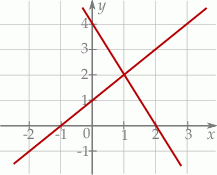
Wskaż ten układ, którego geometryczną interpretację przedstawiono na rysunku.
A) 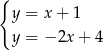 B)
B) 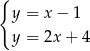 C)
C) 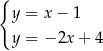 D)
D) 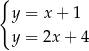
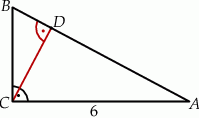
Przyprostokątna 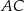 trójkąta prostokątnego
trójkąta prostokątnego 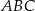 ma długość 6, a wysokość
ma długość 6, a wysokość 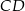 dzieli go na dwa takie trójkąty
dzieli go na dwa takie trójkąty 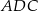 i
i 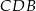 , że pole trójkąta
, że pole trójkąta 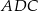 jest 4 razy większe od pola trójkąta
jest 4 razy większe od pola trójkąta 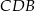 (zobacz rysunek).
(zobacz rysunek).
Przyprostokątna 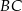 trójkąta prostokątnego
trójkąta prostokątnego 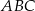 jest równa
jest równa
A) 1,5 B) 2 C) 2,5 D) 3
W trójkącie 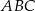 bok
bok 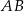 jest 3 razy dłuższy od boku
jest 3 razy dłuższy od boku 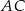 , a długość boku
, a długość boku 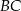 stanowi
stanowi  długości boku
długości boku 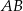 . Oblicz cosinus najmniejszego kąta trójkąta
. Oblicz cosinus najmniejszego kąta trójkąta 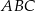 .
.
Pewien turysta pokonał trasę 112 km, przechodząc każdego dnia tę samą liczbę kilometrów. Gdyby mógł przeznaczyć na tę wędrówkę o 3 dni więcej, to w ciągu każdego dnia mógłby przechodzić o 12 km mniej. Oblicz, ile kilometrów dziennie przechodził ten turysta.
Liczba 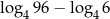 jest równa
jest równa
A) 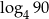 B)
B) 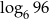 C) 4 D) 2
C) 4 D) 2
Rozwiązanie równania 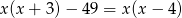 należy do przedziału
należy do przedziału
A) 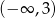 B)
B) 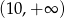 C)
C) 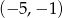 D)
D) 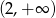
Długości boków czworokąta 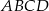 są równe:
są równe: 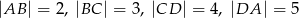 . Na czworokącie
. Na czworokącie 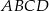 opisano okrąg. Oblicz długość przekątnej
opisano okrąg. Oblicz długość przekątnej 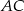 tego czworokąta.
tego czworokąta.
Do zbioru rozwiązań nierówności 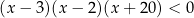 należy liczba
należy liczba
A) 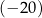 B)
B) 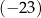 C) 20 D) 23
C) 20 D) 23
Wykaż, że dla każdej liczby rzeczywistej  i dla każdej liczby rzeczywistej
i dla każdej liczby rzeczywistej 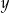 takich, że
takich, że 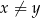 , spełniona jest nierówność
, spełniona jest nierówność
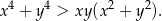
Miejscem zerowym funkcji liniowej 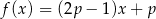 jest liczba
jest liczba 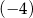 . Wtedy
. Wtedy
A) 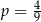 B)
B) 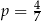 C)
C) 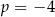 D)
D) 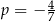
W ciągu arytmetycznym 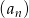 , określonym dla
, określonym dla 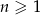 , dane są dwa wyrazy:
, dane są dwa wyrazy: 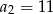 i
i 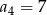 . Suma czterech początkowych wyrazów tego ciągu jest równa
. Suma czterech początkowych wyrazów tego ciągu jest równa
A) 36 B) 40 C) 13 D) 20
Niech 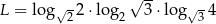 . Wtedy
. Wtedy
A) 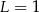 B)
B) 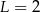 C)
C) 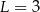 D)
D) 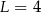
Dany jest ciąg geometryczny 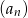 określony wzorem
określony wzorem 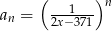 dla
dla 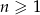 . Wszystkie wyrazy tego ciągu są dodatnie. Wyznacz najmniejszą liczbę całkowitą
. Wszystkie wyrazy tego ciągu są dodatnie. Wyznacz najmniejszą liczbę całkowitą  , dla której nieskończony szereg
, dla której nieskończony szereg 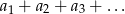 jest zbieżny.
jest zbieżny.
W urnie znajduje się 16 kul, które mogą się różnić wyłącznie kolorem. Wśród nich jest 10 kul białych i 6 kul czarnych. Z tej urny losujemy dwukrotnie jedną kulę bez zwracania. Oblicz prawdopodobieństwo wylosowania dwóch kul białych.
