Liczba 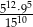 jest równa
jest równa
A) 25 B) 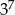 C)
C) 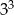 D)
D) 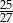
/Szkoła średnia
Funkcja 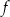 jest określona wzorem
jest określona wzorem 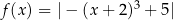 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Zbiorem wartości funkcji
. Zbiorem wartości funkcji 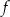 jest przedział
jest przedział
A) 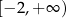 B)
B) 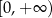 C)
C) 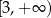 D)
D) 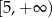
Dana jest funkcja 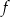 określona wzorem
określona wzorem 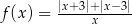 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej 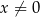 . Wyznacz zbiór wartości tej funkcji.
. Wyznacz zbiór wartości tej funkcji.
Trójwyrazowy ciąg 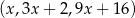 jest geometryczny. Oblicz
jest geometryczny. Oblicz  .
.
Wyznacz wszystkie wartości parametru 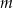 , dla których równanie
, dla których równanie
![2 2 (x− 3)[x + (m − 1)x − 6m + 2m )] = 0](https://img.zadania.info/zad/1637258/HzadT1x.gif)
ma dokładnie dwa rozwiązania.
Rozwiąż nierówność 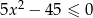 .
.
Nieskończony ciąg geometryczny 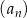 jest określony w następujący sposób:
jest określony w następujący sposób: 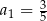 oraz
oraz 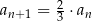 dla
dla 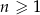 . Suma wszystkich wyrazów tego ciągu jest równa
. Suma wszystkich wyrazów tego ciągu jest równa
A)  B)
B) 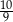 C)
C) 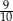 D)
D) 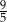
Dany jest kwadrat 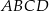 , w którym
, w którym 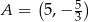 . Przekątna
. Przekątna 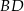 tego kwadratu jest zawarta w prostej o równaniu
tego kwadratu jest zawarta w prostej o równaniu 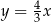 . Oblicz współrzędne punktu przecięcia przekątnych
. Oblicz współrzędne punktu przecięcia przekątnych 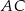 i
i 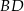 oraz pole kwadratu
oraz pole kwadratu 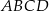 .
.
Rozważamy wszystkie ostrosłupy prawidłowe trójkątne, w których suma wysokości 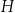 ostrosłupa oraz promienia
ostrosłupa oraz promienia 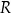 okręgu opisanego na podstawie tego ostrosłupa jest równa 6.
okręgu opisanego na podstawie tego ostrosłupa jest równa 6.
-
Wykaż, że objętość
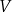 każdego z takich ostrosłupów w zależności od długości
każdego z takich ostrosłupów w zależności od długości 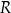 promienia okręgu opisanego na podstawie ostrosłupa jest określona wzorem
promienia okręgu opisanego na podstawie ostrosłupa jest określona wzorem 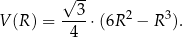
-
Wyznacz długość promienia okręgu opisanego na podstawie tego z rozważanych ostrosłupów, którego objętość jest największa. Oblicz tę największą objętość.
Iloczyn wszystkich rozwiązań równania 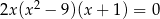 jest równy
jest równy
A) 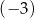 B) 3 C) 0 D) 9
B) 3 C) 0 D) 9
Dane są proste o równaniach 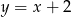 oraz
oraz 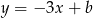 , które przecinają się w punkcie leżącym na osi
, które przecinają się w punkcie leżącym na osi 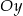 układu współrzędnych. Oblicz pole trójkąta, którego dwa boki zawierają się w danych prostych, a trzeci jest zawarty w osi
układu współrzędnych. Oblicz pole trójkąta, którego dwa boki zawierają się w danych prostych, a trzeci jest zawarty w osi 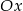 .
.
Dane są punkty 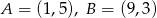 i prosta
i prosta 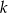 o równaniu
o równaniu 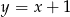 . Oblicz współrzędne punktu
. Oblicz współrzędne punktu 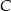 leżącego na prostej
leżącego na prostej 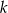 , dla którego suma
, dla którego suma 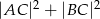 jest najmniejsza.
jest najmniejsza.
Przekrój ostrosłupa prawidłowego trójkątnego 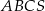 płaszczyzną przechodzącą przez wierzchołek
płaszczyzną przechodzącą przez wierzchołek 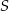 i wysokości dwóch ścian bocznych jest trójkątem równobocznym. Krawędź boczna tego ostrosłupa ma długość
i wysokości dwóch ścian bocznych jest trójkątem równobocznym. Krawędź boczna tego ostrosłupa ma długość 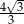 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.
Z liczb ośmioelementowego zbioru 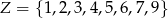 tworzymy ośmiowyrazowy ciąg, którego wyrazy się nie powtarzają. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że żadne dwie liczby parzyste nie są sąsiednimi wyrazami utworzonego ciągu. Wynik przedstaw w postaci ułamka zwykłego nieskracalnego.
tworzymy ośmiowyrazowy ciąg, którego wyrazy się nie powtarzają. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że żadne dwie liczby parzyste nie są sąsiednimi wyrazami utworzonego ciągu. Wynik przedstaw w postaci ułamka zwykłego nieskracalnego.
Pole powierzchni bocznej ostrosłupa prawidłowego czworokątnego jest równe 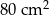 , a pole jego powierzchni całkowitej wynosi
, a pole jego powierzchni całkowitej wynosi 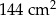 . Oblicz długość krawędzi podstawy i długość krawędzi bocznej tego ostrosłupa. Zapisz obliczenia.
. Oblicz długość krawędzi podstawy i długość krawędzi bocznej tego ostrosłupa. Zapisz obliczenia.
Rozwiąż nierówność: 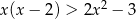 .
.
Ciąg arytmetyczny 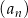 jest określony dla każdej liczby naturalnej
jest określony dla każdej liczby naturalnej 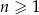 . Różnica tego ciągu jest równa 2. Wtedy
. Różnica tego ciągu jest równa 2. Wtedy
A) 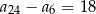 B)
B) 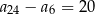 C)
C) 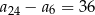 D)
D) 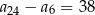
Pierwiastkami wielomianu stopnia trzeciego są liczby 1, 3, 5. Współczynnik przy najwyższej potędze zmiennej tego wielomianu jest równy 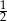 . Uzasadnij, że dla każdej liczby całkowitej nieparzystej wartość tego wielomianu jest liczbą podzielną przez 24.
. Uzasadnij, że dla każdej liczby całkowitej nieparzystej wartość tego wielomianu jest liczbą podzielną przez 24.
Podstawa 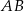 trójkąta równoramiennego
trójkąta równoramiennego 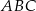 jest zawarta w prostej o równaniu
jest zawarta w prostej o równaniu 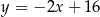 . Wierzchołki
. Wierzchołki 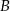 i
i 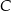 mają współrzędne
mają współrzędne 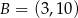 i
i 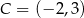 . Oblicz współrzędne wierzchołka
. Oblicz współrzędne wierzchołka 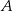 i pole trójkąta
i pole trójkąta 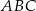 .
.
W kartezjańskim układzie współrzędnych 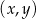 narysowano wykres funkcji
narysowano wykres funkcji 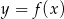 (zobacz rysunek).
(zobacz rysunek).
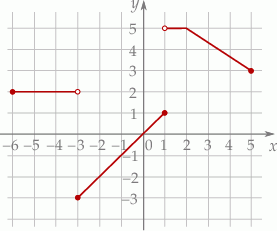
Funkcja 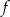 jest malejąca w zbiorze
jest malejąca w zbiorze
A) 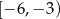 B)
B) ![[− 3,1]](https://img.zadania.info/zad/1700319/HzadT5x.gif) C)
C) ![(1,2]](https://img.zadania.info/zad/1700319/HzadT6x.gif) D)
D) ![[2,5]](https://img.zadania.info/zad/1700319/HzadT7x.gif)

