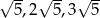Ciąg 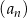 jest określony wzorem
jest określony wzorem 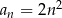 dla
dla 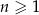 . Różnica
. Różnica 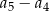 jest równa
jest równa
A) 4 B) 20 C) 36 D) 18
/Szkoła średnia
Liczba 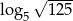 jest równa
jest równa
A)  B) 2 C) 3 D)
B) 2 C) 3 D) 
Zbiorem wszystkich rozwiązań nierówności 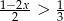 jest przedział
jest przedział
A) 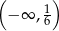 B)
B) 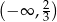 C)
C) 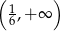 D)
D) 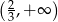
Rzucamy trzy razy symetryczną monetą. Niech 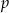 oznacza prawdopodobieństwo otrzymania dokładnie dwóch orłów w tych trzech rzutach. Wtedy
oznacza prawdopodobieństwo otrzymania dokładnie dwóch orłów w tych trzech rzutach. Wtedy
A) 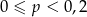 B)
B) 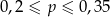 C)
C) 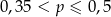 D)
D) 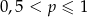
Wyrażenie 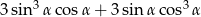 może być przekształcone do postaci
może być przekształcone do postaci
A) 3 B) 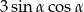 C)
C) 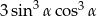 D)
D) 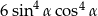
Wyznacz równania prostych stycznych do okręgu o równaniu 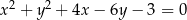 i zarazem prostopadłych do prostej
i zarazem prostopadłych do prostej 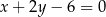 .
.
Ala kupiła trzy zeszyty i blok rysunkowy. Średnia arytmetyczna cen tych czterech artykułów była równa 6 zł. Zeszyty kosztowały łącznie 15 zł. Ile kosztował blok rysunkowy?
A) 4 zł B) 5 zł C) 8 zł D) 9 zł
Na rysunku, w kartezjańskim układzie współrzędnych 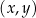 , przedstawiono wykres funkcji
, przedstawiono wykres funkcji 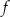 . Każdy z punktów przecięcia wykresu funkcji
. Każdy z punktów przecięcia wykresu funkcji 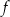 z prostą o równaniu
z prostą o równaniu 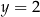 ma obie współrzędne całkowite.
ma obie współrzędne całkowite.
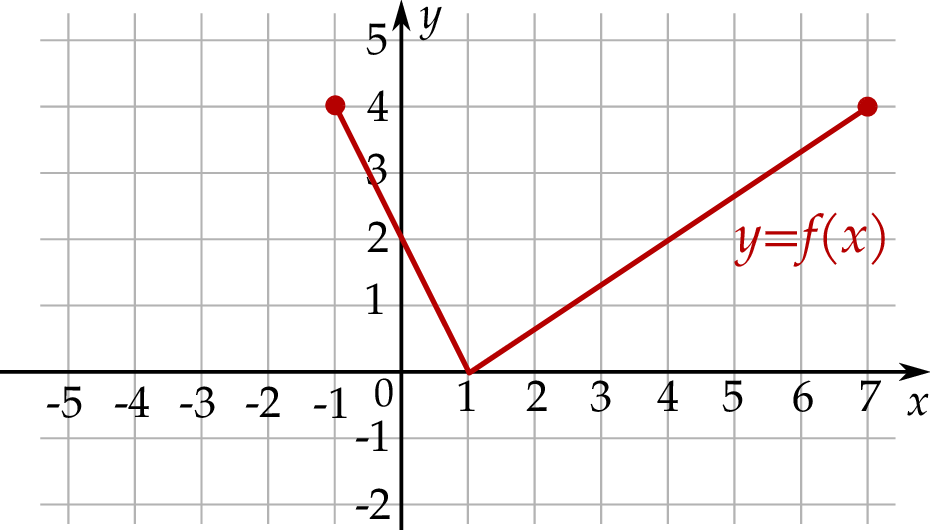
Na kolejnym rysunku przedstawiono wykres funkcji 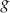 , powstałej w wyniku przesunięcia równoległego wykresu funkcji
, powstałej w wyniku przesunięcia równoległego wykresu funkcji 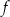 wzdłuż osi
wzdłuż osi 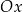 o 4 jednostki w lewo.
o 4 jednostki w lewo.
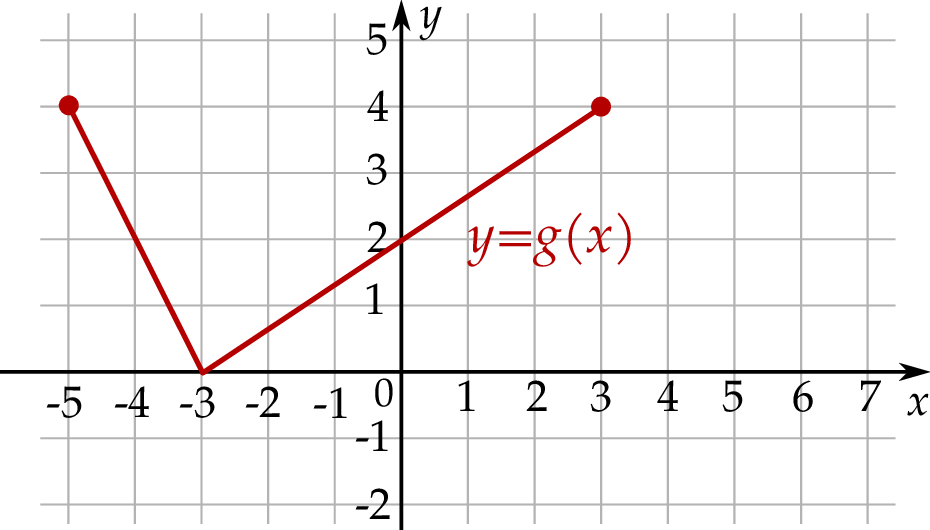
Funkcje 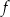 i
i 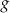 są powiązane zależnością
są powiązane zależnością
A) 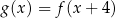 , , | B) 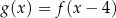 , , | C) 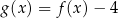 , , |
oraz mają takie same
| 1) dziedziny. | 2) zbiory wartości. |
Rozwiąż nierówność 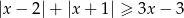 .
.
Rozwiązaniem równania 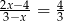 jest liczba
jest liczba
A) 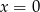 B)
B) 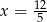 C)
C) 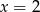 D)
D) 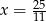
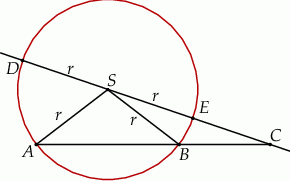
Dany jest okrąg o środku w punkcie 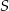 i promieniu
i promieniu  . Na przedłużeniu cięciwy
. Na przedłużeniu cięciwy 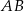 poza punkt
poza punkt 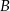 odłożono odcinek
odłożono odcinek 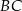 równy promieniowi danego okręgu. Przez punkty
równy promieniowi danego okręgu. Przez punkty 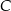 i
i 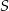 poprowadzono prostą. Prosta
poprowadzono prostą. Prosta 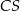 przecina dany okrąg w punktach
przecina dany okrąg w punktach 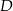 i
i 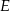 (zobacz rysunek). Wykaż, że jeżeli miara kąta
(zobacz rysunek). Wykaż, że jeżeli miara kąta 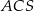 jest równa
jest równa  , to miara kąta
, to miara kąta 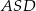 jest równa
jest równa 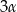 .
.
Dany jest ostrosłup prawidłowy czworokątny o wysokości 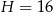 . Cosinus kąta nachylenia krawędzi bocznej do płaszczyzny podstawy tego ostrosłupa jest równy
. Cosinus kąta nachylenia krawędzi bocznej do płaszczyzny podstawy tego ostrosłupa jest równy  . Oblicz pole powierzchni bocznej tego ostrosłupa.
. Oblicz pole powierzchni bocznej tego ostrosłupa.
Dana jest funkcja kwadratowa 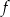 określona wzorem
określona wzorem 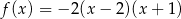 . Funkcja
. Funkcja 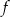 jest rosnąca w zbiorze
jest rosnąca w zbiorze
A) 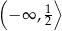 B)
B) 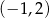 C)
C) 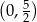 D)
D) 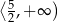
Przekątne równoległoboku mają długości 4 i 8, a kąt między tymi przekątnymi ma miarę 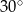 . Pole tego równoległoboku jest równe
. Pole tego równoległoboku jest równe
A) 32 B) 16 C) 12 D) 8
Cosinus kąta ostrego  jest równy
jest równy 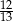 . Wtedy
. Wtedy
A) 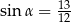 B)
B) 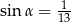 C)
C) 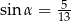 D)
D) 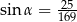
Kąt  jest ostry oraz
jest ostry oraz 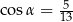 . Wtedy
. Wtedy
A) 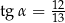 B)
B) 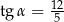 C)
C) 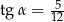 D)
D) 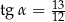
Dane są dwa podzbiory zbioru liczb całkowitych:
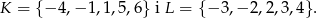
Z każdego z nich losujemy jedną liczbę. Oblicz prawdopodobieństwo zdarzenia polegającego na wylosowaniu liczb, których iloczyn jest dodatni.
Okrąg przedstawiony na rysunku ma środek w punkcie 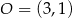 i przechodzi przez punkty
i przechodzi przez punkty 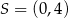 i
i 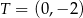 . Okrąg ten jest opisany przez równanie
. Okrąg ten jest opisany przez równanie
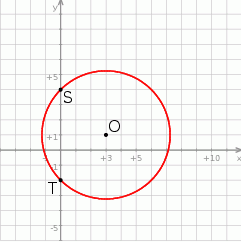
A) 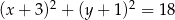 B)
B) 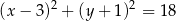
C) 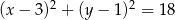 D)
D) 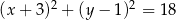
Wykaż, że dla dowolnych różnych liczb rzeczywistych  i
i 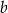 prawdziwa jest nierówność
prawdziwa jest nierówność
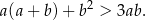
Dany jest trójkąt o bokach długości 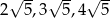 . Trójkątem podobnym do tego trójkąta jest trójkąt, którego boki mają długości
. Trójkątem podobnym do tego trójkąta jest trójkąt, którego boki mają długości
A) 10, 15, 20 B) 20, 45, 80 C) 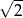 ,
, 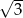 ,
, 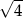 D)
D)