Na rysunku przedstawiono fragment wykresu funkcji kwadratowej 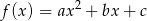 , której miejsca zerowe to:
, której miejsca zerowe to: 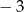 i 1.
i 1.
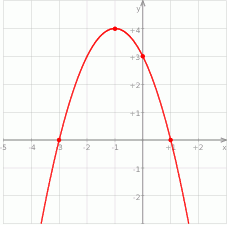
Współczynnik  we wzorze funkcji
we wzorze funkcji 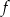 jest równy
jest równy
A) 1 B) 2 C) 3 D) 4
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Na rysunku przedstawiono fragment wykresu funkcji kwadratowej 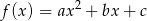 , której miejsca zerowe to:
, której miejsca zerowe to: 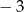 i 1.
i 1.

Współczynnik  we wzorze funkcji
we wzorze funkcji 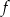 jest równy
jest równy
A) 1 B) 2 C) 3 D) 4
Rozwiąż równanie
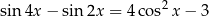
w zbiorze ![[0,2π ]](https://img.zadania.info/zad/1452081/HzadT1x.png) .
.
Podstawą ostrosłupa 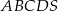 jest kwadrat
jest kwadrat 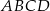 . Krawędź boczna
. Krawędź boczna 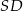 jest wysokością ostrosłupa, a jej długość jest dwa razy większa od długości krawędzi podstawy. Oblicz sinus kąta między ścianami bocznymi
jest wysokością ostrosłupa, a jej długość jest dwa razy większa od długości krawędzi podstawy. Oblicz sinus kąta między ścianami bocznymi 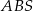 i
i 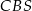 tego ostrosłupa.
tego ostrosłupa.
Oblicz najmniejszą i największą wartość funkcji kwadratowej 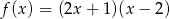 w przedziale
w przedziale 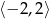 .
.
Oblicz granicę 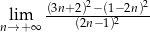 .
.
Cena pewnego towaru wraz z 7–procentowym podatkiem VAT jest równa 34 347 zł. Cena tego samego towaru wraz z 23–procentowym podatkiem VAT będzie równa
A) 37 236 zł B) 39 842,52 zł C) 39 483 zł D) 42 246,81 zł
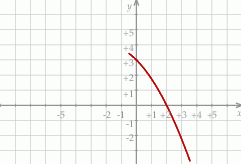
Na rysunku przedstawiono fragment wykresu funkcji kwadratowej 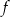 . Jednym z miejsc zerowych tej funkcji jest liczba 2. Do wykresu funkcji
. Jednym z miejsc zerowych tej funkcji jest liczba 2. Do wykresu funkcji 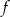 należy punkt
należy punkt 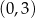 . Prosta o równaniu
. Prosta o równaniu 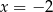 jest osią symetrii paraboli, będącej wykresem funkcji
jest osią symetrii paraboli, będącej wykresem funkcji 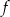 .
.
Drugim miejscem zerowym funkcji 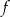 jest liczba
jest liczba
A) 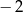 B)
B) 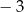 C)
C) 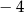 D)
D) 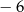
W kartezjańskim układzie współrzędnych 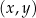 zaznaczono kąt
zaznaczono kąt  o wierzchołku w punkcie
o wierzchołku w punkcie 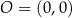 . Jedno z ramion tego kąta pokrywa się z dodatnią półosią
. Jedno z ramion tego kąta pokrywa się z dodatnią półosią 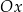 , a drugie przechodzi przez punkt
, a drugie przechodzi przez punkt 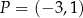 (zobacz rysunek).
(zobacz rysunek).
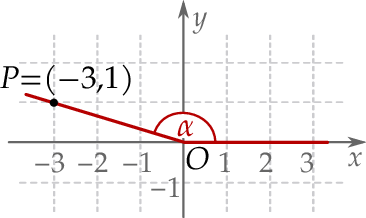
Tangens kąta  jest równy
jest równy
A) 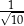 B)
B) 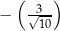 C)
C) 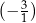 D)
D) 
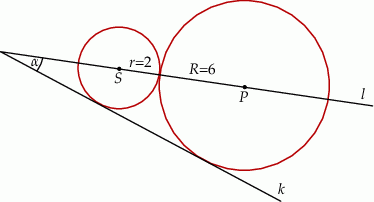
Dwa okręgi o promieniach 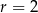 i
i 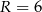 są styczne zewnętrznie i są styczne do wspólnej prostej
są styczne zewnętrznie i są styczne do wspólnej prostej 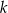 . Wykaż, że prosta
. Wykaż, że prosta 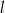 przechodząca przez środki
przechodząca przez środki 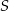 i
i 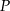 tych okręgów przecina prostą
tych okręgów przecina prostą 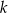 pod kątem
pod kątem 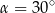 (zobacz rysunek).
(zobacz rysunek).
W tabeli przedstawiono roczne przyrosty wysokości pewnej sosny w ciągu sześciu kolejnych lat.
| kolejne lata | 1 | 2 | 3 | 4 | 5 | 6 |
| przyrost (w cm) | 10 | 10 | 7 | 8 | 8 | 7 |
Oblicz średni roczny przyrost wysokości tej sosny w badanym okresie sześciu lat. Otrzymany wynik zaokrąglij do 1 cm. Oblicz błąd względny otrzymanego przybliżenia. Podaj ten błąd w procentach.
Liczby  i
i  są dodatnie. Liczba
są dodatnie. Liczba 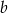 stanowi 48% liczby
stanowi 48% liczby  oraz 32% liczby
oraz 32% liczby  . Wynika stąd, że
. Wynika stąd, że
A) 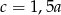 B)
B) 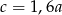 C)
C) 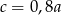 D)
D) 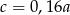
Wskaż równanie prostej równoległej do prostej o równaniu 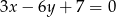 .
.
A) 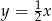 B)
B) 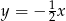 C)
C) 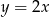 D)
D) 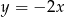
Dany jest sześcian 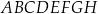 o krawędzi długości 6. Punkt
o krawędzi długości 6. Punkt 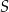 jest punktem przecięcia przekątnych
jest punktem przecięcia przekątnych 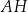 i
i 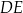 ściany bocznej
ściany bocznej 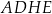 (zobacz rysunek).
(zobacz rysunek).
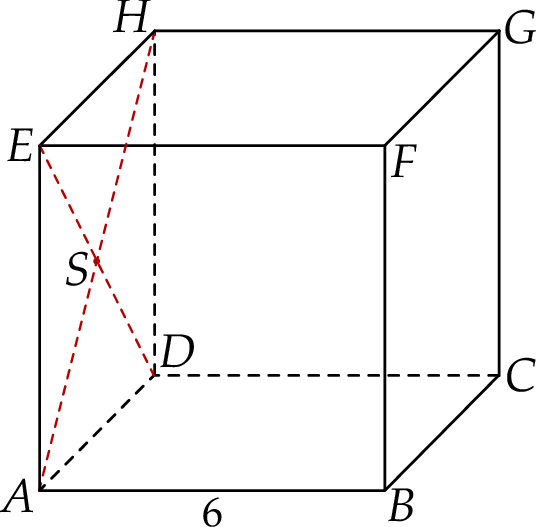
Oblicz wysokość trójkąta 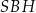 poprowadzoną z punktu
poprowadzoną z punktu 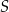 na bok
na bok 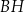 tego trójkąta.
tego trójkąta.
W pewnym ostrosłupie prawidłowym stosunek liczby 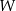 wszystkich wierzchołków do liczby
wszystkich wierzchołków do liczby 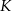 wszystkich krawędzi jest równy
wszystkich krawędzi jest równy 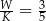 . Podstawą tego ostrosłupa jest
. Podstawą tego ostrosłupa jest
A) kwadrat. B) pięciokąt foremny.
C) sześciokąt foremny. D) siedmiokąt foremny.
Rozwiąż nierówność 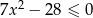 .
.
Średnia arytmetyczna pięciu liczb: 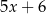 ,
, 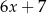 ,
, 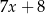 ,
, 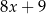 ,
, 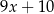 , jest równa 8. Wtedy
, jest równa 8. Wtedy  jest równe
jest równe
A) 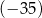 B) 0 C) 0,35 D) 35
B) 0 C) 0,35 D) 35
Każda krawędź graniastosłupa prawidłowego sześciokątnego ma długość równą 6. Pole powierzchni całkowitej tego graniastosłupa jest równe
A) 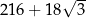 B)
B) 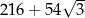 C)
C) 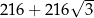 D)
D) 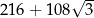
W grupie liczącej 29 uczniów (dziewcząt i chłopców) jest 15 chłopców. Z tej grupy trzeba wylosować jedną osobę. Prawdopodobieństwo zdarzenia polegającego na tym, że zostanie wylosowana dziewczyna, jest równe
A) 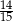 B)
B) 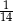 C)
C) 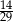 D)
D) 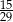
Dany jest stożek o objętości 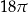 , którego przekrojem osiowym jest trójkąt
, którego przekrojem osiowym jest trójkąt 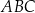 (zobacz rysunek). Kąt
(zobacz rysunek). Kąt 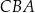 jest kątem nachylenia tworzącej
jest kątem nachylenia tworzącej 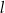 tego stożka do płaszczyzny jego podstawy. Tangens kąta
tego stożka do płaszczyzny jego podstawy. Tangens kąta 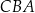 jest równy 2.
jest równy 2.
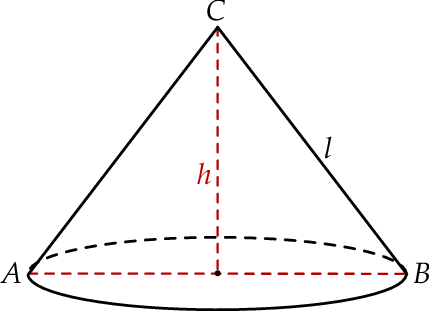
Wynika stąd, że wysokość 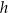 tego stożka jest równa
tego stożka jest równa
A) 12 B) 6 C) 4 D) 2
Prosta 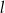 , na której leży punkt
, na której leży punkt 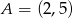 , przecina parabolę o równaniu
, przecina parabolę o równaniu 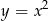 w dwóch różnych punktach
w dwóch różnych punktach 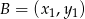 i
i 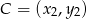 . Oblicz wartość współczynnika kierunkowego prostej
. Oblicz wartość współczynnika kierunkowego prostej 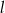 , przy której suma
, przy której suma 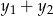 osiągnie wartość najmniejszą.
osiągnie wartość najmniejszą.
