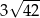Ciąg 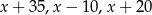 jest geometryczny. Stąd wynika, że
jest geometryczny. Stąd wynika, że
A) 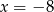 B)
B) 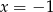 C)
C) 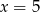 D)
D) 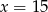
/Szkoła średnia
Dany jest romb o boku długości 4 i kącie rozwartym 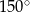 . Pole tego rombu jest równe
. Pole tego rombu jest równe
A) 8 B) 12 C) 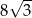 D) 16
D) 16
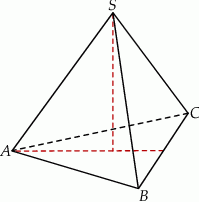
Objętość ostrosłupa prawidłowego trójkątnego  (tak jak na rysunku) jest równa 72, a promień okręgu wpisanego w podstawę
(tak jak na rysunku) jest równa 72, a promień okręgu wpisanego w podstawę  tego ostrosłupa jest równy 2. Oblicz tangens kąta między wysokością tego ostrosłupa i jego ścianą boczną.
tego ostrosłupa jest równy 2. Oblicz tangens kąta między wysokością tego ostrosłupa i jego ścianą boczną.
Dane są punkty 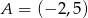 oraz
oraz 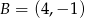 . Promień okręgu opisanego na trójkącie równobocznym
. Promień okręgu opisanego na trójkącie równobocznym 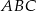 jest równy
jest równy
A) 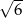 B)
B) 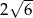 C)
C) 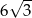 D)
D) 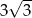
Funkcja liniowa 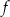 jest określona wzorem
jest określona wzorem 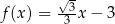 . W kartezjańskim układzie współrzędnych
. W kartezjańskim układzie współrzędnych 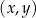 wykres funkcji
wykres funkcji 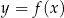 jest prostą nachyloną do osi
jest prostą nachyloną do osi 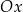 pod kątem ostrym
pod kątem ostrym  . Oblicz
. Oblicz  .
.
Na rysunku przedstawiono fragment wykresu funkcji kwadratowej 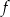 .
.
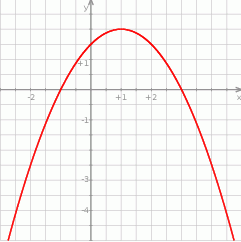
Funkcja 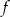 jest określona wzorem
jest określona wzorem
A) 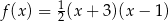 B)
B) 
C) 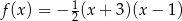 D)
D) 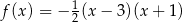
Rozwiąż nierówność 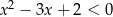 .
.
Dany jest ciąg geometryczny 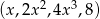 o wyrazach nieujemnych. Wtedy
o wyrazach nieujemnych. Wtedy
A) 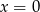 B)
B) 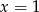 C)
C) 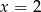 D)
D) 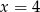
Wyznacz wszystkie wartości parametru 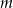 , dla których równanie
, dla których równanie 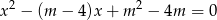 ma dwa różne pierwiastki rzeczywiste, których suma jest mniejsza od
ma dwa różne pierwiastki rzeczywiste, których suma jest mniejsza od 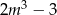 .
.
Dane są ciągi 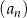 ,
, 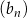 ,
, 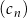 ,
, 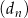 , określone dla każdej liczby naturalnej
, określone dla każdej liczby naturalnej 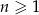 wzorami:
wzorami: 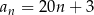 ,
, 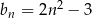 ,
, 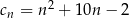 ,
, 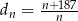 . Liczba 197 jest dziesiątym wyrazem ciągu
. Liczba 197 jest dziesiątym wyrazem ciągu
A) 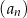 B)
B) 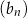 C)
C) 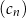 D)
D) 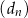
Funkcja 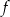 jest określona dla każdej liczby rzeczywistej
jest określona dla każdej liczby rzeczywistej  wzorem
wzorem 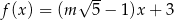 . Ta funkcja jest rosnąca dla każdej liczby
. Ta funkcja jest rosnąca dla każdej liczby 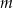 spełniającej warunek
spełniającej warunek
A) 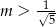 B)
B) 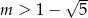 C)
C) 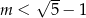 D)
D) 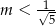
W pojemniku jest siedem kul: pięć kul białych i dwie kule czarne. Z tego pojemnika losujemy jednocześnie dwie kule bez zwracania. Następnie – z kul pozostałych w pojemniku – losujemy jeszcze jedną kulę. Oblicz prawdopodobieństwo wylosowania kuli czarnej w drugim losowaniu.
Liczba 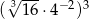 jest równa
jest równa
A) 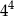 B)
B) 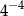 C)
C) 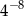 D)
D) 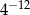
Liczba 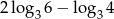 jest równa
jest równa
A) 4 B) 2 C) 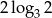 D)
D) 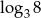
Rozwiąż nierówność 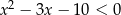 .
.
W pewnej klasie stosunek liczby dziewcząt do liczby chłopców jest równy 4:5. Losujemy jedną osobę z tej klasy. Prawdopodobieństwo tego, że będzie to dziewczyna, jest równe
A) 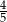 B)
B)  C)
C) 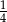 D)
D) 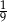
Wykaż, że dla każdej liczby rzeczywistej dodatniej  prawdziwa jest nierówność
prawdziwa jest nierówność
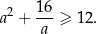
Dla każdej liczby rzeczywistej  wyrażenie
wyrażenie 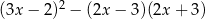 jest po uproszczeniu równe
jest po uproszczeniu równe
A) 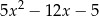 B)
B) 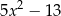 C)
C) 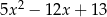 D)
D) 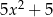
Wykaż, że dla każdej liczby rzeczywistej  i każdej liczby rzeczywistej
i każdej liczby rzeczywistej 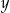 takich, że
takich, że 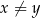 prawdziwa jest nierówność
prawdziwa jest nierówność
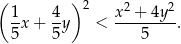
Pole powierzchni całkowitej graniastosłupa prawidłowego czworokątnego, w którym wysokość jest 3 razy dłuższa od krawędzi podstawy, jest równe 140. Zatem krawędź podstawy tego graniastosłupa jest równa
A) 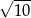 B)
B) 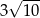 C)
C) 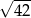 D)
D)