Rozpatrujemy wszystkie walce, których pole powierzchni całkowitej jest równe 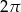 . Oblicz promień podstawy tego walca, który ma największą objętość. Podaj tę największą objętość.
. Oblicz promień podstawy tego walca, który ma największą objętość. Podaj tę największą objętość.
/Szkoła średnia
Trzywyrazowy ciąg 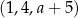 jest arytmetyczny. Liczba
jest arytmetyczny. Liczba  jest równa
jest równa
A) 0 B) 7 C) 2 D) 11
Średnice 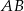 i
i 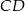 okręgu o środku
okręgu o środku 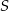 przecinają się pod kątem
przecinają się pod kątem 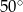 (tak jak na rysunku).
(tak jak na rysunku).
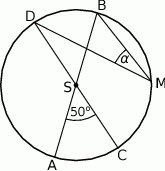
Miara kąta  jest równa
jest równa
A) 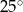 B)
B) 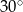 C)
C) 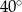 D)
D) 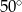
Medianą zestawu danych  jest liczba 4. Wtedy
jest liczba 4. Wtedy  może być równe
może być równe
A) 2 B) 3 C) 4 D) 5
Dla ciągu arytmetycznego 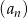 , określonego dla
, określonego dla 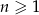 , spełniony jest warunek
, spełniony jest warunek 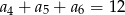 . Wtedy
. Wtedy
A) 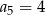 B)
B) 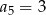 C)
C) 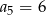 D)
D) 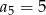
Dany jest trójkąt prostokątny 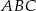 . Na przyprostokątnych
. Na przyprostokątnych 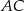 i
i 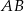 tego trójkąta obrano odpowiednio punkty
tego trójkąta obrano odpowiednio punkty 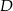 i
i 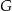 . Na przeciwprostokątnej
. Na przeciwprostokątnej 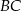 wyznaczono punkty
wyznaczono punkty 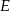 i
i 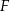 takie, że
takie, że 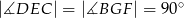 (zobacz rysunek). Wykaż, że trójkąt
(zobacz rysunek). Wykaż, że trójkąt 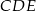 jest podobny do trójkąta
jest podobny do trójkąta 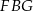 .
.
Funkcja 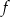 określona jest wzorem
określona jest wzorem 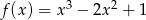 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Wyznacz równania tych stycznych do wykresu funkcji
. Wyznacz równania tych stycznych do wykresu funkcji 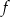 , które są równoległe do prostej o równaniu
, które są równoległe do prostej o równaniu 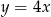 .
.
Dany jest kwadrat 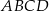 . Przekątne
. Przekątne 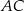 i
i 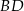 przecinają się w punkcie
przecinają się w punkcie 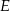 . Punkty
. Punkty 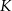 i
i 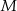 są środkami odcinków – odpowiednio –
są środkami odcinków – odpowiednio – 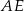 i
i 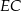 . Punkty
. Punkty 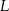 i
i 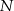 leżą na przekątnej
leżą na przekątnej 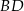 tak, że
tak, że 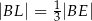 i
i 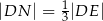 (zobacz rysunek). Wykaż, że stosunek pola czworokąta
(zobacz rysunek). Wykaż, że stosunek pola czworokąta 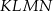 do pola kwadratu
do pola kwadratu 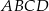 jest równy 1:3.
jest równy 1:3.
Dany jest ciąg 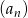 określony wzorem
określony wzorem 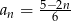 dla
dla 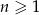 . Ciąg ten jest
. Ciąg ten jest
A) arytmetyczny i jego różnica jest równa 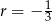 .
.
B) arytmetyczny i jego różnica jest równa 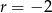 .
.
C) geometryczny i jego iloraz jest równy 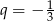 .
.
D) geometryczny i jego iloraz jest równy 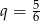 .
.
Ciąg arytmetyczny 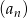 jest określony wzorem
jest określony wzorem 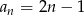 , dla
, dla 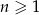 . Suma stu początkowych kolejnych wyrazów tego ciągu jest równa
. Suma stu początkowych kolejnych wyrazów tego ciągu jest równa
A) 9900 B) 9950 C) 10000 D) 10050
Wyznacz wszystkie wartości parametru 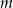 , dla których równanie
, dla których równanie 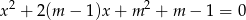 ma dwa różne pierwiastki rzeczywiste
ma dwa różne pierwiastki rzeczywiste 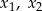 takie, że
takie, że 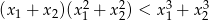 .
.
Wśród 100 osób przeprowadzono ankietę, w której zadano pytanie o liczbę książek przeczytanych w ostatnim roku. Wyniki ankiety zebrano w poniższej tabeli.
| Liczba książek | 0 | 1 | 2 | 3 | 4 | 5 |
| Liczba osób | 23 | 14 | 28 | 17 | 11 | 7 |
Średnia liczba przeczytanych książek przez jedną ankietowaną osobę jest równa
A) 0,5 B) 1 C) 2 D) 2,5
W trójkącie prostokątnym równoramiennym 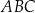 o przeciwprostokątnej
o przeciwprostokątnej 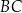 punkt
punkt 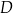 jest środkiem ramienia
jest środkiem ramienia 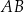 . Odcinek
. Odcinek 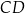 ma długość 5 (zobacz rysunek).
ma długość 5 (zobacz rysunek).
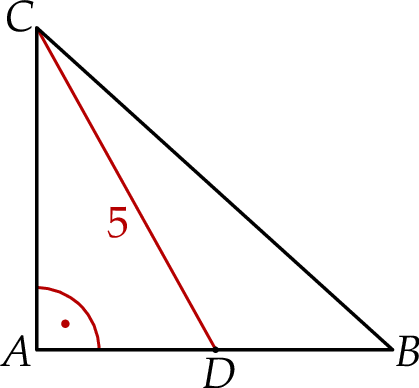
Oblicz obwód trójkąta 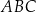 .
.
W skarbcu królewskim było 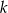 monet. Pierwszego dnia rano skarbnik dorzucił 25 monet, a każdego następnego ranka dorzucał o 2 monety więcej niż dnia poprzedniego. Jednocześnie ze skarbca król zabierał w południe każdego dnia 50 monet. Oblicz najmniejszą liczbę
monet. Pierwszego dnia rano skarbnik dorzucił 25 monet, a każdego następnego ranka dorzucał o 2 monety więcej niż dnia poprzedniego. Jednocześnie ze skarbca król zabierał w południe każdego dnia 50 monet. Oblicz najmniejszą liczbę 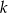 , dla której w każdym dniu w skarbcu była co najmniej jedna moneta, a następnie dla tej wartości
, dla której w każdym dniu w skarbcu była co najmniej jedna moneta, a następnie dla tej wartości 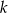 oblicz, w którym dniu w skarbcu była najmniejsza liczba monet.
oblicz, w którym dniu w skarbcu była najmniejsza liczba monet.
Czternasty wyraz ciągu arytmetycznego jest równy 8, a różnica tego ciągu jest równa 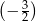 . Siódmy wyraz tego ciągu jest równy
. Siódmy wyraz tego ciągu jest równy
A) 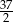 B)
B) 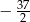 C)
C) 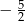 D)
D) 
Rozwiąż nierówność 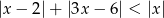 .
.
Liczba 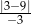 jest równa
jest równa
A) 2 B) 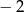 C) 0 D)
C) 0 D) 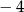
Liczba 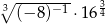 jest równa
jest równa
A) 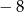 B)
B) 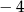 C) 2 D) 4
C) 2 D) 4
Tworząca stożka o promieniu podstawy 3 ma długość 6 (zobacz rysunek).
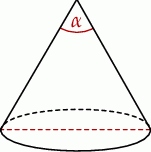
Kąt  rozwarcia tego stożka jest równy
rozwarcia tego stożka jest równy
A) 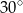 B)
B) 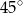 C)
C) 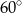 D)
D) 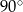
Rozważamy wszystkie kody czterocyfrowe utworzone tylko z cyfr 1, 3, 6, 8, przy czym w każdym kodzie każda z tych cyfr występuje dokładnie jeden raz. Liczba wszystkich takich kodów jest równa
A) 4 B) 10 C) 24 D) 16

