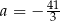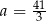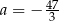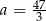Funkcja 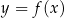 jest określona za pomocą tabeli
jest określona za pomocą tabeli
 | 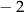 | 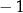 | 0 | 1 | 2 |
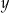 | 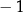 | 0 | 1 | 0 | 3 |
Wskaż zdanie prawdziwe.
A) Funkcja 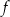 ma dokładnie jedno miejsce zerowe.
ma dokładnie jedno miejsce zerowe.
B) W układzie współrzędnych 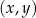 wykres funkcji
wykres funkcji 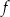 jest symetryczny względem osi
jest symetryczny względem osi 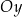 .
.
C) Największa wartość funkcji 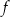 jest równa 3.
jest równa 3.
D) Najmniejsza wartość funkcji 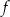 jest równa
jest równa 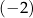 .
.

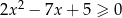 .
.  ciąg
ciąg 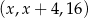 jest geometryczny. Liczba
jest geometryczny. Liczba  jest równa
jest równa 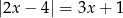 w zbiorze liczb rzeczywistych
w zbiorze liczb rzeczywistych 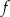 oraz
oraz 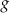 , określone wzorami
, określone wzorami 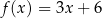 oraz
oraz 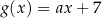 , mają to samo miejsce zerowe. Współczynnik
, mają to samo miejsce zerowe. Współczynnik  we wzorze funkcji
we wzorze funkcji 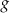 jest równy
jest równy 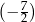
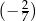


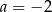 i
i 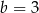 . Wartość wyrażenia
. Wartość wyrażenia 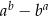 jest równa
jest równa 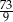
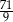
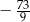
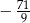
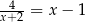 .
. 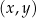 dany jest równoległobok
dany jest równoległobok 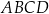 , w którym
, w którym 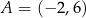 oraz
oraz 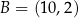 . Przekątne
. Przekątne 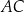 oraz
oraz 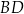 tego równoległoboku przecinają się w punkcie
tego równoległoboku przecinają się w punkcie 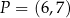 . Oblicz długość boku
. Oblicz długość boku 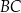 tego równoległoboku.
tego równoległoboku. 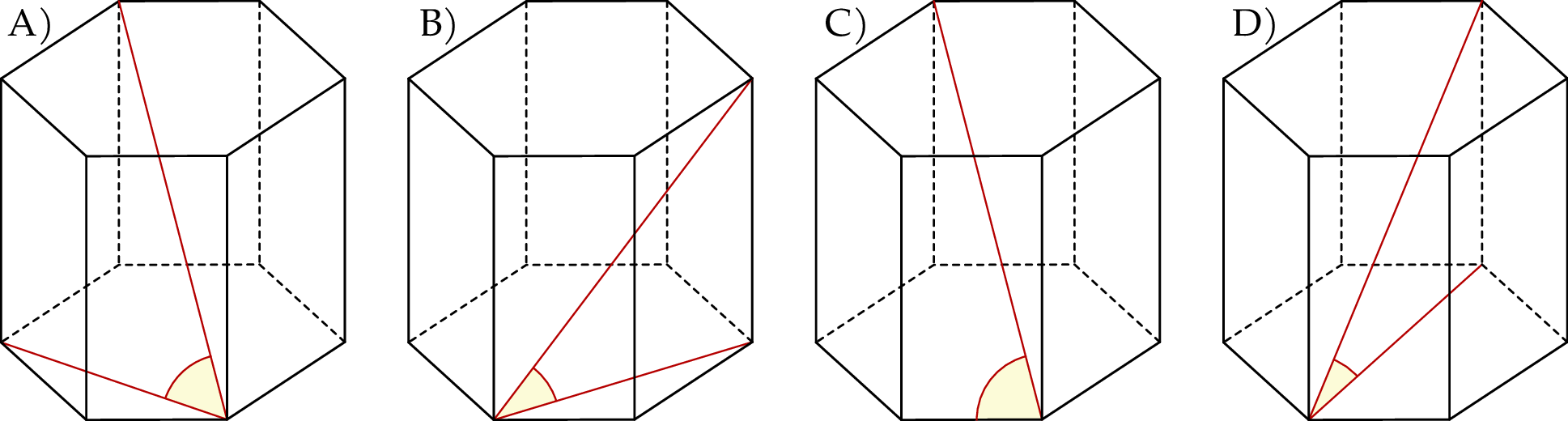
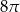
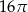
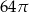
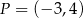 i
i 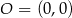 leżą na jednej prostej. Kąt
leżą na jednej prostej. Kąt  jest kątem nachylenia tej prostej do osi
jest kątem nachylenia tej prostej do osi 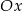 (zobacz rysunek).
(zobacz rysunek). 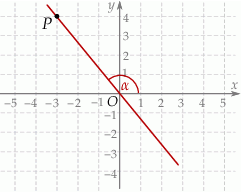
 jest równy
jest równy 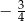
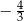
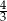
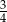
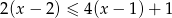 jest
jest 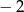
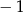
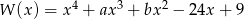 jest kwadratem wielomianu
jest kwadratem wielomianu 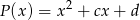 . Oblicz
. Oblicz  oraz
oraz 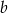 .
. 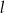 , na której leży punkt
, na której leży punkt 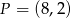 , tworzy z dodatnimi półosiami układu współrzędnych trójkąt prostokątny o polu równym 36. Wyznacz równanie prostej
, tworzy z dodatnimi półosiami układu współrzędnych trójkąt prostokątny o polu równym 36. Wyznacz równanie prostej 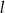 .
. 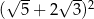 jest równa
jest równa 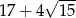
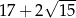
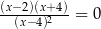 ma dokładnie
ma dokładnie 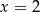
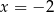
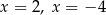
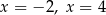
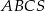 jest trójkąt równoboczny
jest trójkąt równoboczny 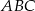 . Wysokość
. Wysokość 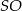 tego ostrosłupa jest równa wysokości jego podstawy. Objętość tego ostrosłupa jest równa 27. Oblicz pole powierzchni bocznej ostrosłupa
tego ostrosłupa jest równa wysokości jego podstawy. Objętość tego ostrosłupa jest równa 27. Oblicz pole powierzchni bocznej ostrosłupa 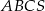 oraz cosinus kąta, jaki tworzą wysokość ściany bocznej i płaszczyzna podstawy ostrosłupa.
oraz cosinus kąta, jaki tworzą wysokość ściany bocznej i płaszczyzna podstawy ostrosłupa. 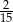
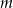 , dla których równanie
, dla których równanie 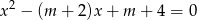 ma dwa różne pierwiastki rzeczywiste
ma dwa różne pierwiastki rzeczywiste 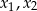 takie, że
takie, że 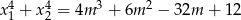 .
. 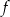 jest określona wzorem
jest określona wzorem 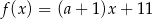 , gdzie
, gdzie  to pewna liczba rzeczywista, ma miejsce zerowe równe
to pewna liczba rzeczywista, ma miejsce zerowe równe 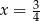 . Stąd wynika, że
. Stąd wynika, że