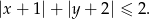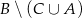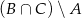Sprawdź, czy liczby 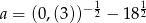 ,
, 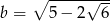 ,
, 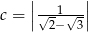 są w podanej kolejności kolejnymi wyrazami ciągu arytmetycznego.
są w podanej kolejności kolejnymi wyrazami ciągu arytmetycznego.
/Szkoła średnia
Rozwiąż równanie 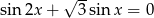 w przedziale
w przedziale 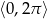 .
.
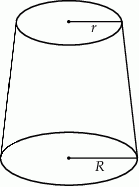
Objętość stożka ściętego (przedstawionego na rysunku) można obliczyć ze wzoru 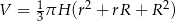 , gdzie
, gdzie  i
i 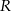 są promieniami podstaw (
są promieniami podstaw (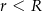 ), a
), a 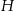 jest wysokością bryły. Dany jest stożek ścięty, którego wysokość jest równa 10, objętość
jest wysokością bryły. Dany jest stożek ścięty, którego wysokość jest równa 10, objętość 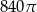 , a
, a 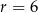 . Oblicz cosinus kąta nachylenia przekątnej przekroju osiowego tej bryły do jednej z jej podstaw.
. Oblicz cosinus kąta nachylenia przekątnej przekroju osiowego tej bryły do jednej z jej podstaw.
Oblicz granicę
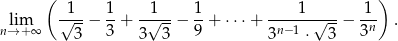
Oblicz granicę
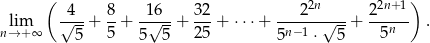
We wnętrzu sześcianu umieszczono czworościan foremny w ten sposób, że wszystkie krawędzie czworościanu są przekątnymi ścian bocznych sześcianu. Wyznacz stosunek objętości czworościanu do objętości sześcianu.
Równanie 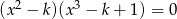 nie ma rozwiązań niewymiernych. Liczba
nie ma rozwiązań niewymiernych. Liczba 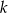 może być równa
może być równa
A) 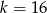 B)
B) 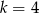 C)
C) 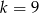 D)
D) 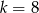
Zbiór rozwiązań nierówności 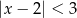 jest taki sam jak zbiór rozwiązań nierówności
jest taki sam jak zbiór rozwiązań nierówności
A) 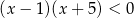 B)
B) 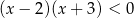
C) 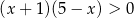 D)
D) 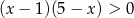
Zbiór rozwiązań nierówności 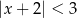 jest taki sam jak zbiór rozwiązań nierówności
jest taki sam jak zbiór rozwiązań nierówności
A) 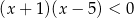 B)
B) 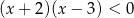
C) 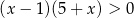 D)
D) 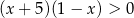
Przedział 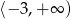 jest zbiorem rozwiązań nierówności
jest zbiorem rozwiązań nierówności
A) 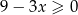 B)
B) 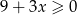 C)
C) 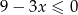 D)
D) 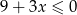
Przedział 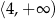 jest zbiorem rozwiązań nierówności
jest zbiorem rozwiązań nierówności
A) 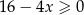 B)
B) 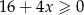 C)
C) 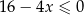 D)
D) 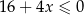
Dana jest funkcja 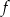 określona wzorem
określona wzorem 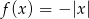 . Ta funkcja przyjmuje wartości ujemne dla
. Ta funkcja przyjmuje wartości ujemne dla
A) 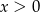 B)
B) 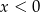 C)
C) 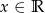 D)
D) 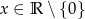
Dana jest funkcja 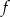 określona wzorem
określona wzorem 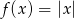 . Ta funkcja przyjmuje wartości dodatnie dla
. Ta funkcja przyjmuje wartości dodatnie dla
A) 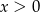 B)
B) 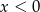 C)
C) 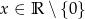 D)
D) 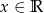
Dana jest funkcja 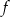 określona wzorem
określona wzorem 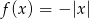 . Ta funkcja przyjmuje wartości niedodatnie dla
. Ta funkcja przyjmuje wartości niedodatnie dla
A) 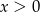 B)
B) 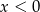 C)
C) 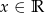 D)
D) 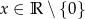
Środek 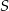 okręgu o równaniu
okręgu o równaniu 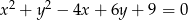 ma współrzędne
ma współrzędne
A) 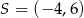 B)
B) 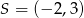 C)
C) 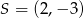 D)
D) 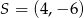
Środek okręgu o równaniu 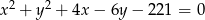 ma współrzędne
ma współrzędne
A) 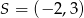 B)
B) 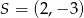 C)
C) 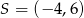 D)
D) 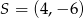
Środek 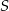 okręgu o równaniu
okręgu o równaniu 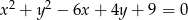 ma współrzędne
ma współrzędne
A) 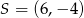 B)
B) 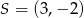 C)
C) 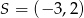 D)
D) 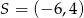
Środek 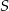 okręgu o równaniu
okręgu o równaniu 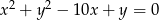 ma współrzędne
ma współrzędne
A) 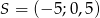 B)
B) 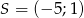 C)
C) 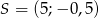 D)
D) 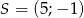
Środek 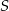 okręgu o równaniu
okręgu o równaniu 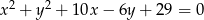 ma współrzędne
ma współrzędne
A) 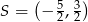 B)
B) 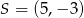 C)
C) 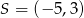 D)
D) 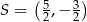
Środek 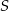 okręgu o równaniu
okręgu o równaniu 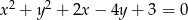 ma współrzędne
ma współrzędne
A) 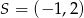 B)
B) 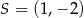 C)
C) 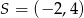 D)
D) 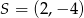
Środkiem okręgu o równaniu 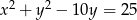 jest punkt
jest punkt
A) 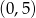 B)
B) 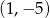 C)
C) 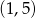 D)
D) 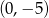
Dane są zbiory: 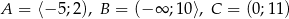 . Zapisz w postaci przedziału lub sumy przedziałów zbiory:
. Zapisz w postaci przedziału lub sumy przedziałów zbiory:
Kąt  jest ostry i
jest ostry i 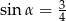 . Wówczas
. Wówczas
A) 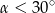 B)
B) 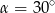 C)
C) 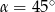 D)
D) 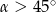
Jeśli  jest kątem ostrym i
jest kątem ostrym i 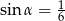 , to
, to
A) 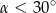 B)
B) 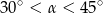 C)
C) 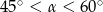 D)
D) 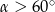
Kąt  jest ostry oraz
jest ostry oraz 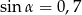 . Zatem
. Zatem
A) 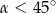 B)
B) 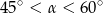 C)
C) 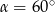 D)
D) 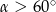
Kąt  jest ostry i
jest ostry i 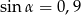 . Wówczas
. Wówczas
A) 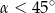 B)
B) 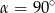 C)
C) 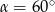 D)
D) 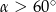
Zbiór 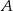 jest zbiorem rozwiązań nierówności
jest zbiorem rozwiązań nierówności 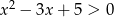 . Zatem
. Zatem
A) 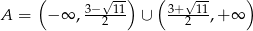 B)
B) 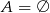 C)
C) 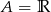 D)
D) 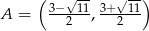
Zbiór 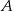 jest zbiorem rozwiązań nierówności
jest zbiorem rozwiązań nierówności 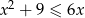 . Zatem
. Zatem
A) 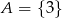 B)
B) 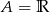 C)
C) 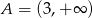 D)
D) 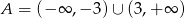
Zbiór 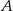 jest zbiorem rozwiązań nierówności
jest zbiorem rozwiązań nierówności 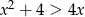 . Zatem
. Zatem
A) 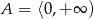 B)
B) 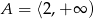 C)
C) 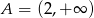 D)
D) 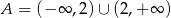
Zbiór 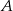 jest zbiorem rozwiązań nierówności
jest zbiorem rozwiązań nierówności 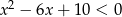 . Zatem
. Zatem
A) 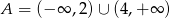 B)
B) 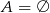 C)
C) 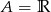 D)
D) 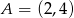
Zbiór 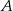 jest zbiorem rozwiązań nierówności
jest zbiorem rozwiązań nierówności 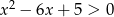 . Zatem
. Zatem
A) 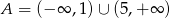 B)
B) 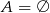 C)
C) 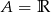 D)
D) 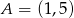
Zbiór 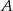 jest zbiorem rozwiązań nierówności
jest zbiorem rozwiązań nierówności 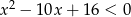 . Zatem
. Zatem
A) 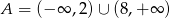 B)
B) 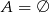 C)
C) 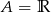 D)
D) 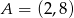
Dana jest funkcja kwadratowa 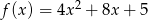 . Zbiorem rozwiązań nierówności
. Zbiorem rozwiązań nierówności 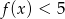 jest
jest
A) 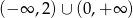 B)
B) 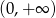 C)
C) 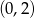 D)
D) 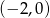
Zbiorem rozwiązań nierówności 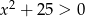 jest
jest
A) 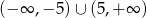 B)
B) 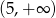 C)
C) 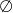 D)
D) 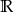
Koło 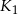 ma promień długości
ma promień długości  . Wewnątrz tego koła rysujemy kolejno koła
. Wewnątrz tego koła rysujemy kolejno koła 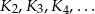 takie, że kolejne koło ma średnicę równą promieniowi poprzedniego koła.
takie, że kolejne koło ma średnicę równą promieniowi poprzedniego koła.
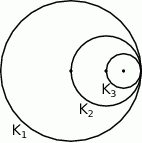
Wyznacz pole koła 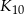 .
.
Rozwiąż równanie 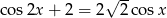 .
.
Rozwiąż równanie 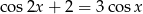 .
.
Rozwiąż równanie 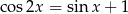 w przedziale
w przedziale 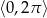 .
.
Rozwiąż równanie 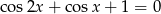 dla
dla 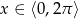 .
.
Rozwiąż równanie 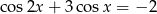 w przedziale
w przedziale 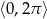 .
.
Do zbioru rozwiązań nierówności 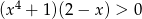 nie należy liczba
nie należy liczba
A) 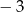 B)
B) 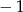 C) 1 D) 3
C) 1 D) 3
Do zbioru rozwiązań nierówności 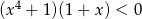 nie należy liczba
nie należy liczba
A) 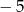 B)
B) 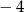 C)
C) 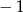 D)
D) 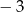
W pewnej loterii fantowej przygotowano dwie urny z losami, przy czym w drugiej urnie było trzy razy więcej losów niż w pierwszej urnie. Prawdopodobieństwo wybrania losu wygrywającego z pierwszej urny jest równe 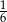 , a prawdopodobieństwo wybrania losu wygrywającego z drugiej urny jest równe
, a prawdopodobieństwo wybrania losu wygrywającego z drugiej urny jest równe 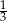 . Przed rozpoczęciem loterii losy z obu urn zmieszano i umieszczono w jednej urnie. Po tej operacji prawdopodobieństwo wybrania losu wygrywającego jest równe
. Przed rozpoczęciem loterii losy z obu urn zmieszano i umieszczono w jednej urnie. Po tej operacji prawdopodobieństwo wybrania losu wygrywającego jest równe
A) 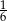 B)
B) 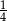 C)
C) 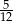 D)
D) 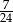
W pewnej loterii fantowej przygotowano dwie urny z losami, przy czym w drugiej urnie było trzy razy więcej losów niż w pierwszej urnie. Prawdopodobieństwo wybrania losu wygrywającego z pierwszej urny jest równe  , a prawdopodobieństwo wybrania losu wygrywającego z drugiej urny jest równe
, a prawdopodobieństwo wybrania losu wygrywającego z drugiej urny jest równe 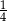 . Przed rozpoczęciem loterii losy z obu urn zmieszano i umieszczono w jednej urnie. Po tej operacji prawdopodobieństwo wybrania losu wygrywającego jest równe
. Przed rozpoczęciem loterii losy z obu urn zmieszano i umieszczono w jednej urnie. Po tej operacji prawdopodobieństwo wybrania losu wygrywającego jest równe
A) 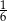 B)
B) 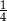 C)
C) 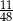 D)
D) 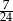
Pole równoległoboku 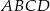 o danych wierzchołkach
o danych wierzchołkach 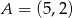 i
i 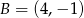 jest równe 26. Wyznacz współrzędne pozostałych wierzchołków równoległoboku, jeżeli jego przekątne przecinają się w punkcie leżącym na prostej
jest równe 26. Wyznacz współrzędne pozostałych wierzchołków równoległoboku, jeżeli jego przekątne przecinają się w punkcie leżącym na prostej 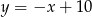 , który ma obie współrzędne będące liczbami całkowitymi.
, który ma obie współrzędne będące liczbami całkowitymi.
Oblicz pole ośmiokąta foremnego wpisanego w okrąg o promieniu 6.
Narysuj w układzie współrzędnych zbiór punktów spełniających nierówność: