W trójkącie prostokątnym przeciwprostokątna ma długość 4. Pole koła opisanego na tym trójkącie wynosi
A) 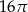 B)
B) 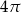 C)
C) 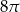 D)
D) 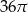
/Szkoła średnia
Pole koła opisanego na trójkącie prostokątnym o bokach długości 10, 24, 26 jest równe
A) 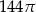 B)
B) 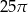 C)
C) 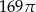 D)
D) 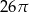
Rysunek przedstawia wykres funkcji 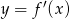 .
.
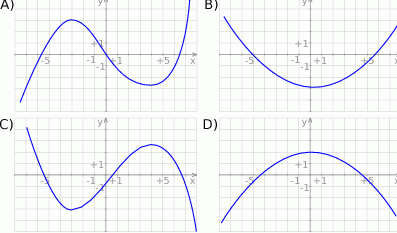
Wskaż wykres funkcji  .
.
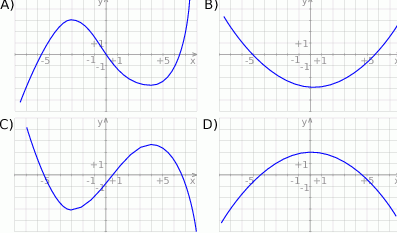
Rysunek przedstawia wykres funkcji 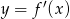 .
.
Wskaż wykres funkcji  .
.
Wszystkich liczb całkowitych dodatnich spełniających nierówność 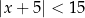 jest
jest
A) 9 B) 10 C) 20 D) 21
Wszystkich liczb całkowitych ujemnych spełniających nierówność 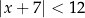 jest
jest
A) 19 B) 23 C) 18 D) 24
Rozwiąż układ równań 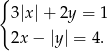
Liczba wszystkich dodatnich liczb pięciocyfrowych, które są podzielne przez 3, i których cyfry należą do zbioru 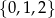 , jest równa
, jest równa
A) 81 B) 54 C) 162 D) 243
Jedno z rozwiązań równania 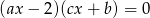 jest równe 6. Ciąg
jest równe 6. Ciąg  jest ciągiem arytmetycznym, w którym pierwszy wyraz jest o 8 większy od trzeciego. Znajdź drugie rozwiązanie tego równania.
jest ciągiem arytmetycznym, w którym pierwszy wyraz jest o 8 większy od trzeciego. Znajdź drugie rozwiązanie tego równania.
Wzór funkcji liniowej, której wykresem jest prosta nachylona do osi 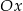 pod kątem o mierze
pod kątem o mierze 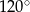 i przechodzi przez punkt
i przechodzi przez punkt 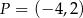 jest postaci
jest postaci
A) 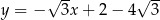 B)
B) 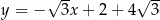
C) 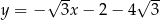 D)
D) 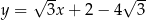
Wykres funkcji liniowej 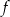 jest nachylony do osi
jest nachylony do osi 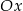 pod kątem
pod kątem 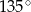 . Wiadomo, że
. Wiadomo, że 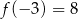 . Funkcja liniowa
. Funkcja liniowa  jest określona wzorem
jest określona wzorem
A) 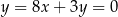 B)
B) 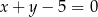
C) 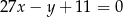 D)
D) 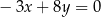
Objętość sześcianu jest równa 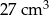 . Jaka jest suma długości wszystkich krawędzi tego sześcianu?
. Jaka jest suma długości wszystkich krawędzi tego sześcianu?
A) 18 cm B) 36 cm C) 24 cm D) 12 cm
Objętość sześcianu jest równa 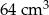 . Jaka jest suma długości wszystkich krawędzi tego sześcianu?
. Jaka jest suma długości wszystkich krawędzi tego sześcianu?
A) 48 cm B) 36 cm C) 24 cm D) 64 cm
Dane są wektory: ![→ u = [2;− 4]](https://img.zadania.info/zad/9899559/HzadT0x.gif) ,
, ![→ v = [− 3;5]](https://img.zadania.info/zad/9899559/HzadT1x.gif) . Oblicz
. Oblicz 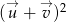 .
.
Dane są wektory: ![→ u = [2;− 4]](https://img.zadania.info/zad/2354795/HzadT0x.gif) ,
, ![→ v = [− 3;5]](https://img.zadania.info/zad/2354795/HzadT1x.gif) . Oblicz
. Oblicz 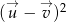 .
.
Dane są wektory: ![→ u = [2;− 4]](https://img.zadania.info/zad/7943696/HzadT0x.gif) ,
, ![→ v = [− 3;5]](https://img.zadania.info/zad/7943696/HzadT1x.gif) . Oblicz
. Oblicz 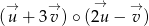 .
.
Dane są dwie funkcje liniowe określone wzorami 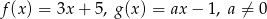 . Funkcje te mają wspólne miejsce zerowe. Wynika stąd, że
. Funkcje te mają wspólne miejsce zerowe. Wynika stąd, że
A) 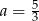 B)
B) 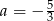 C)
C) 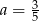 D)
D) 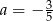
Dane są dwie funkcje liniowe określone wzorami 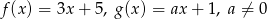 . Funkcje te mają wspólne miejsce zerowe. Wynika stąd, że
. Funkcje te mają wspólne miejsce zerowe. Wynika stąd, że
A) 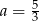 B)
B) 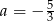 C)
C) 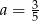 D)
D) 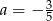
Funkcja liniowa 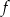 określona wzorem
określona wzorem 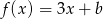 ma takie samo miejsce zerowe, jakie ma funkcja liniowa
ma takie samo miejsce zerowe, jakie ma funkcja liniowa 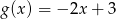 . Stąd wynika, że
. Stąd wynika, że
A) 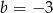 B)
B) 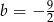 C)
C) 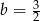 D)
D) 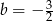
Funkcja liniowa 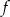 określona wzorem
określona wzorem 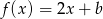 ma takie samo miejsce zerowe, jakie ma funkcja liniowa
ma takie samo miejsce zerowe, jakie ma funkcja liniowa 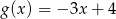 . Stąd wynika, że
. Stąd wynika, że
A) 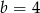 B)
B) 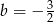 C)
C) 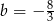 D)
D) 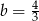
Funkcje liniowe 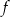 i
i 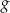 określone wzorami
określone wzorami 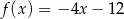 i
i 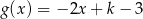 mają wspólne miejsce zerowe. Stąd wynika, że
mają wspólne miejsce zerowe. Stąd wynika, że
A) 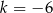 B)
B) 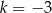 C)
C) 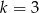 D)
D) 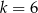
Dane są dwie funkcje liniowe określone wzorami 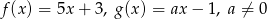 . Funkcje te mają wspólne miejsce zerowe. Wynika stąd, że
. Funkcje te mają wspólne miejsce zerowe. Wynika stąd, że
A) 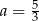 B)
B) 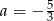 C)
C) 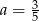 D)
D) 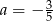
Funkcje liniowe 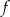 i
i 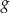 określone wzorami
określone wzorami 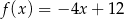 i
i 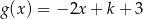 mają wspólne miejsce zerowe. Stąd wynika, że
mają wspólne miejsce zerowe. Stąd wynika, że
A) 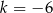 B)
B) 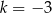 C)
C) 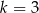 D)
D) 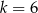
Liczba  jest odwrotnością liczby
jest odwrotnością liczby 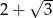 , zaś
, zaś 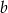 jest liczbą przeciwną do liczby
jest liczbą przeciwną do liczby 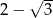 . Różnica
. Różnica 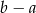 jest wówczas równa:
jest wówczas równa:
A) 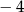 B)
B) 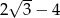 C)
C) 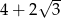 D) 0
D) 0
Średnica 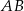 i cięciwa
i cięciwa 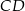 okręgu o środku
okręgu o środku 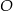 i promieniu
i promieniu  przecinają się w punkcie
przecinają się w punkcie 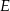 takim, że
takim, że 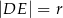 . Wykaż, że
. Wykaż, że 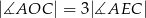 .
.
Dany jest okrąg o środku w punkcie  i promieniu
i promieniu  . Na przedłużeniu cięciwy
. Na przedłużeniu cięciwy  poza punkt
poza punkt 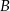 odłożono odcinek
odłożono odcinek 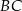 równy promieniowi danego okręgu. Przez punkty
równy promieniowi danego okręgu. Przez punkty 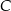 i
i 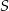 poprowadzono prostą. Prosta
poprowadzono prostą. Prosta 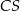 przecina dany okrąg w punktach
przecina dany okrąg w punktach 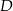 i
i 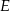 (zobacz rysunek). Wykaż, że jeżeli miara kąta
(zobacz rysunek). Wykaż, że jeżeli miara kąta 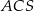 jest równa
jest równa  , to miara kąta
, to miara kąta 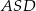 jest równa
jest równa  .
.
Trójkąt 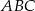 przedstawiony na poniższym rysunku jest równoboczny, a punkty
przedstawiony na poniższym rysunku jest równoboczny, a punkty 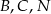 są współliniowe. Na boku
są współliniowe. Na boku 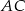 wybrano punkt
wybrano punkt 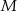 tak, że
tak, że 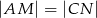 . Wykaż, że
. Wykaż, że 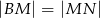 .
.
Wykaż, że wielomian 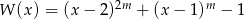 jest podzielny przez wielomian
jest podzielny przez wielomian 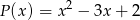 dla każdego
dla każdego 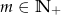 .
.
Liczba punktów wspólnych wykresu funkcji wymiernej 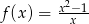 z osią
z osią  jest równa
jest równa
A) 3 B) 2 C) 1 D) 0
Liczba punktów wspólnych wykresu funkcji wymiernej 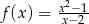 z osią
z osią  jest równa
jest równa
A) 3 B) 2 C) 1 D) 0
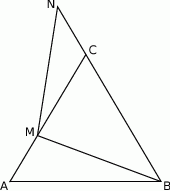
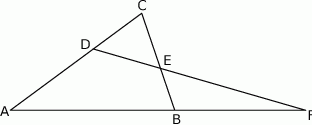
Dany jest trójkąt 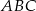 , w którym
, w którym 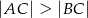 . Na bokach
. Na bokach 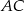 i
i 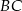 tego trójkąta obrano odpowiednio takie punkty
tego trójkąta obrano odpowiednio takie punkty 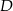 i
i 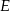 , że
, że 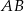 i
i 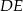 przecinają się w punkcie
przecinają się w punkcie 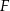 (zobacz rysunek). Wykaż, że jeżeli
(zobacz rysunek). Wykaż, że jeżeli 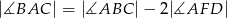 , to
, to 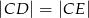 .
.
W pewnej grupie 100 uczniów przeprowadzono sondaż dotyczący dziennego czasu korzystania z komputera. Wyniki sondażu przedstawia poniższy diagram. Na osi poziomej podano – wyrażony w godzinach – dzienny czas korzystania przez ucznia z komputera. Na osi pionowej przedstawiono liczbę uczniów, którzy dziennie korzystają z komputera przez określony czas.
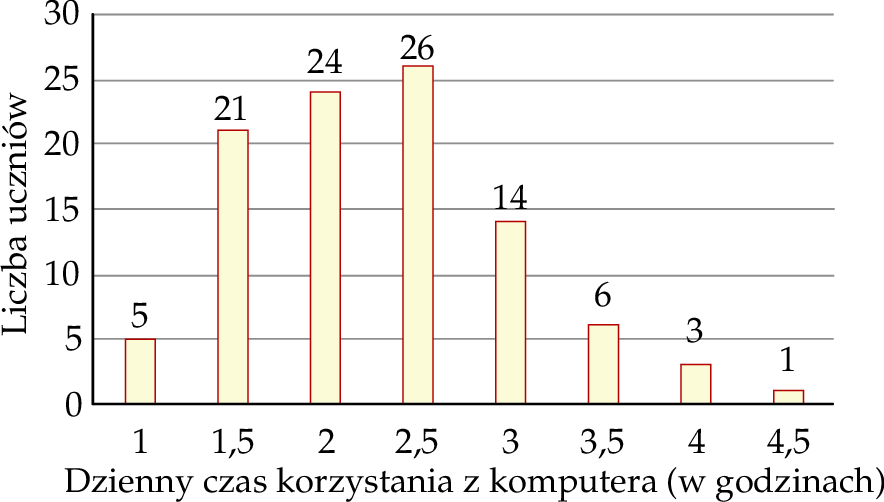
Dominanta dziennego czasu korzystania przez ucznia z komputera jest równa
A) 2,25 godziny B) 2,50 godziny C) 2,75 godziny D) 1,50 godziny
W pewnej grupie 100 uczniów przeprowadzono sondaż dotyczący dziennego czasu korzystania z komputera. Wyniki sondażu przedstawia poniższy diagram. Na osi poziomej podano – wyrażony w godzinach – dzienny czas korzystania przez ucznia z komputera. Na osi pionowej przedstawiono liczbę uczniów, którzy dziennie korzystają z komputera przez określony czas.
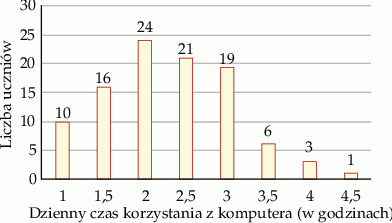
Dominanta dziennego czasu korzystania przez ucznia z komputera jest równa
A) 2,25 godziny B) 2,50 godziny C) 1,5 godziny D) 2 godziny
Jeżeli 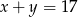 i
i 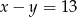 to
to
A) 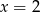 B)
B) 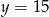 C)
C) 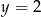 D)
D) 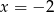
Jeżeli 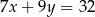 i
i 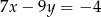 to
to
A) 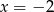 B)
B) 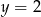 C)
C) 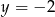 D)
D) 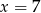
Cena długopisu po 3 podwyżkach o 50% i dwóch obniżkach o 20% wzrosła o 2,32 zł. Nowa cena długopisu jest równa
A) 3,42 zł B) 2 zł C) 4,32 zł D) 2,34 zł
Cena długopisu po 2 podwyżkach o 20% i trzech obniżkach o 50% zmalała o 2,87 zł. Nowa cena długopisu jest równa
A) 1,26 zł B) 0,63 zł C) 3,50 zł D) 6,37 zł
Cena telewizora po 3 podwyżkach o 25% i dwóch obniżkach o 20% wzrosła o 1200 zł. Nowa cena telewizora jest równa
A) 4800 zł B) 5760 zł C) 6000 zł D) 4500 zł
Czwarty wyraz ciągu arytmetycznego jest równy 6. Oblicz sumę siedmiu początkowych wyrazów tego ciągu.

