Trójkąt 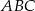 przedstawiony na poniższym rysunku jest równoboczny, a punkty
przedstawiony na poniższym rysunku jest równoboczny, a punkty 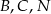 są współliniowe. Na boku
są współliniowe. Na boku 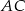 wybrano punkt
wybrano punkt 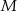 tak, że
tak, że 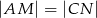 . Wykaż, że
. Wykaż, że 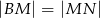 .
.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Trójkąt 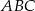 przedstawiony na poniższym rysunku jest równoboczny, a punkty
przedstawiony na poniższym rysunku jest równoboczny, a punkty 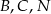 są współliniowe. Na boku
są współliniowe. Na boku 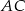 wybrano punkt
wybrano punkt 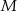 tak, że
tak, że 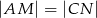 . Wykaż, że
. Wykaż, że 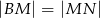 .
.

Wykaż, że wielomian 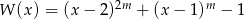 jest podzielny przez wielomian
jest podzielny przez wielomian 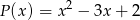 dla każdego
dla każdego 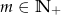 .
.
Liczba punktów wspólnych wykresu funkcji wymiernej 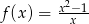 z osią
z osią  jest równa
jest równa
A) 3 B) 2 C) 1 D) 0
Liczba punktów wspólnych wykresu funkcji wymiernej 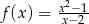 z osią
z osią  jest równa
jest równa
A) 3 B) 2 C) 1 D) 0
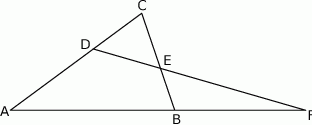
Dany jest trójkąt 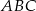 , w którym
, w którym 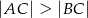 . Na bokach
. Na bokach 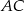 i
i 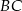 tego trójkąta obrano odpowiednio takie punkty
tego trójkąta obrano odpowiednio takie punkty 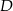 i
i 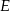 , że
, że 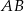 i
i 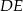 przecinają się w punkcie
przecinają się w punkcie 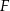 (zobacz rysunek). Wykaż, że jeżeli
(zobacz rysunek). Wykaż, że jeżeli 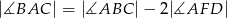 , to
, to 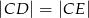 .
.
W pewnej grupie 100 uczniów przeprowadzono sondaż dotyczący dziennego czasu korzystania z komputera. Wyniki sondażu przedstawia poniższy diagram. Na osi poziomej podano – wyrażony w godzinach – dzienny czas korzystania przez ucznia z komputera. Na osi pionowej przedstawiono liczbę uczniów, którzy dziennie korzystają z komputera przez określony czas.
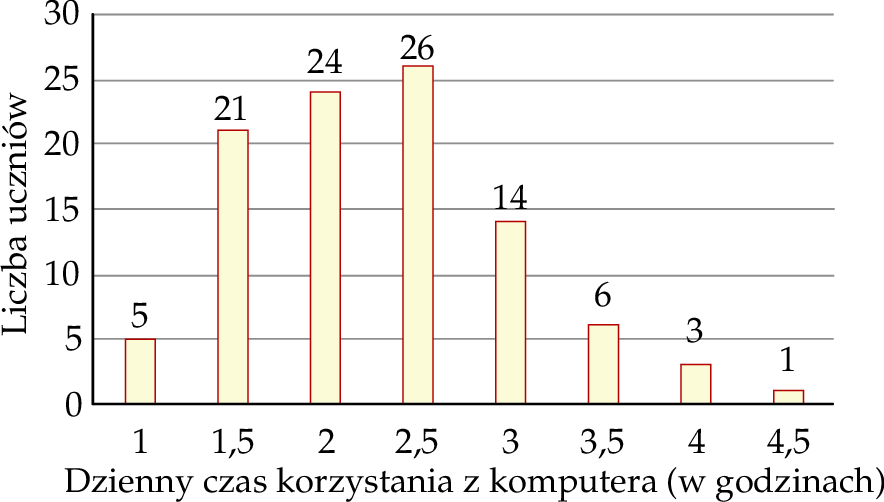
Dominanta dziennego czasu korzystania przez ucznia z komputera jest równa
A) 2,25 godziny B) 2,50 godziny C) 2,75 godziny D) 1,50 godziny
W pewnej grupie 100 uczniów przeprowadzono sondaż dotyczący dziennego czasu korzystania z komputera. Wyniki sondażu przedstawia poniższy diagram. Na osi poziomej podano – wyrażony w godzinach – dzienny czas korzystania przez ucznia z komputera. Na osi pionowej przedstawiono liczbę uczniów, którzy dziennie korzystają z komputera przez określony czas.
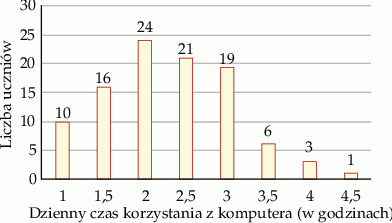
Dominanta dziennego czasu korzystania przez ucznia z komputera jest równa
A) 2,25 godziny B) 2,50 godziny C) 1,5 godziny D) 2 godziny
Jeżeli 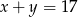 i
i 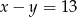 to
to
A) 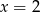 B)
B) 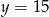 C)
C) 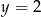 D)
D) 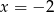
Jeżeli 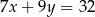 i
i 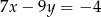 to
to
A) 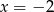 B)
B) 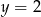 C)
C) 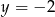 D)
D) 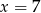
Cena długopisu po 3 podwyżkach o 50% i dwóch obniżkach o 20% wzrosła o 2,32 zł. Nowa cena długopisu jest równa
A) 3,42 zł B) 2 zł C) 4,32 zł D) 2,34 zł
Cena długopisu po 2 podwyżkach o 20% i trzech obniżkach o 50% zmalała o 2,87 zł. Nowa cena długopisu jest równa
A) 1,26 zł B) 0,63 zł C) 3,50 zł D) 6,37 zł
Cena telewizora po 3 podwyżkach o 25% i dwóch obniżkach o 20% wzrosła o 1200 zł. Nowa cena telewizora jest równa
A) 4800 zł B) 5760 zł C) 6000 zł D) 4500 zł
Czwarty wyraz ciągu arytmetycznego jest równy 6. Oblicz sumę siedmiu początkowych wyrazów tego ciągu.
Dany jest nieskończony ciąg geometryczny 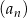 określony dla
określony dla 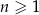 , w którym
, w którym 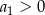 . Suma
. Suma 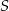 wszystkich wyrazów tego ciągu jest skończona i spełnia nierówność
wszystkich wyrazów tego ciągu jest skończona i spełnia nierówność 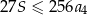 . Wyznacz iloraz tego ciągu.
. Wyznacz iloraz tego ciągu.
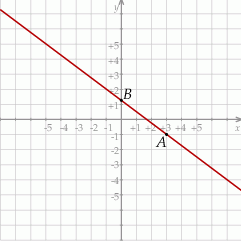
Na rysunku przedstawiony jest fragment wykresu funkcji liniowej 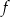 . Na wykresie tej funkcji leżą punkty
. Na wykresie tej funkcji leżą punkty 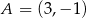 i
i 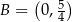 .
.
Obrazem prostej  przy obrocie o kąt
przy obrocie o kąt 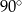 wokół punktu
wokół punktu 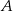 jest wykres funkcji
jest wykres funkcji 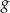 określonej wzorem
określonej wzorem
A) 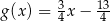 B)
B) 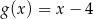 C)
C) 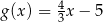 D)
D) 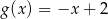
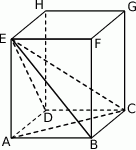
W graniastosłupie prawidłowym czworokątnym  przekątna
przekątna 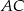 podstawy ma długość 4. Kąt
podstawy ma długość 4. Kąt 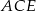 jest równy
jest równy 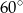 . Oblicz objętość ostrosłupa
. Oblicz objętość ostrosłupa 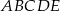 przedstawionego na poniższym rysunku.
przedstawionego na poniższym rysunku.
Jeśli liczbę  powiększymy o 3, to otrzymamy
powiększymy o 3, to otrzymamy  tej liczby. Wynika stąd, że
tej liczby. Wynika stąd, że
A) 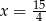 B)
B) 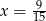 C)
C) 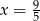 D)
D) 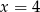
Jeśli liczbę  powiększymy o 5, to otrzymamy
powiększymy o 5, to otrzymamy  tej liczby. Wynika stąd, że
tej liczby. Wynika stąd, że
A) 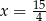 B)
B) 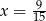 C)
C) 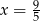 D)
D) 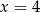
Jeśli liczbę  powiększymy o 4, to otrzymamy
powiększymy o 4, to otrzymamy 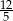 tej liczby. Wynika stąd, że
tej liczby. Wynika stąd, że
A) 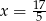 B)
B) 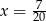 C)
C) 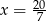 D)
D) 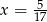
Na rysunku przedstawiono okrąg wpisany w trójkąt.
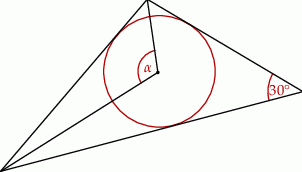
Miara kąta  jest równa
jest równa
A) 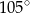 B)
B) 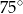 C)
C) 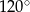 D)
D) 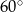
Okrąg o środku w punkcie 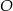 jest wpisany w trójkąt
jest wpisany w trójkąt 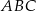 . Wiadomo, że
. Wiadomo, że  i
i  (zobacz rysunek).
(zobacz rysunek).
Miara kąta 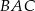 jest równa
jest równa
A) 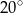 B)
B) 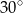 C)
C) 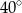 D)
D) 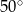
Okrąg o środku w punkcie 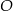 jest wpisany w trójkąt
jest wpisany w trójkąt 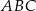 . Wiadomo, że
. Wiadomo, że 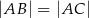 i
i 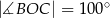 (zobacz rysunek).
(zobacz rysunek).
Miara kąta  jest równa
jest równa
A)  B)
B) 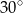 C)
C) 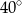 D)
D) 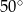
Odległość między środkami okręgów o równaniach 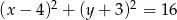 oraz
oraz 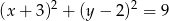 jest równa
jest równa
A) 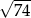 B)
B) 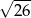 C)
C) 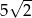 D)
D) 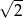
Liczba 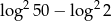 jest równa
jest równa
A) 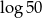 B)
B) 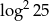 C)
C) 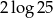 D)
D) 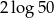
Liczba 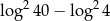 jest równa
jest równa
A) 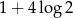 B)
B) 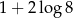 C)
C) 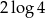 D)
D) 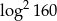
Liczba 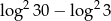 jest równa
jest równa
A) 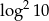 B)
B) 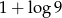 C)
C) 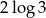 D)
D) 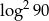
Liczba 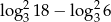 jest równa
jest równa
A) 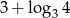 B)
B) 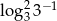 C)
C) 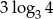 D)
D) 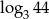
Liczba 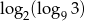 jest równa
jest równa
A) 1 B) 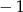 C) 2 D)
C) 2 D) 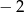
Liczba 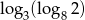 jest równa
jest równa
A) 1 B) 2 C) 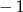 D)
D) 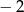
Liczba 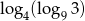 jest równa
jest równa
A) 1 B) 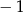 C)
C) 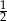 D)
D) 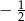
Dany jest okrąg o promieniu 11 oraz punkt 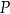 oddalony o 7 od środka okręgu. Przez punkt
oddalony o 7 od środka okręgu. Przez punkt 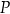 poprowadzono cięciwę o długości 18. W jakim stosunku punkt
poprowadzono cięciwę o długości 18. W jakim stosunku punkt 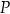 podzielił tę cięciwę na dwa odcinki?
podzielił tę cięciwę na dwa odcinki?
Liczb naturalnych siedmiocyfrowych, w zapisie których występuje dokładnie raz cyfra 7, dokładnie dwa razy cyfra 4, nie występuje cyfra zero, a pozostałe cyfry są między sobą różne jest
A) 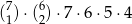 B)
B) 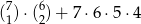 C)
C) 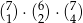 D)
D) 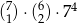
Przyprostokątne trójkąta prostokątnego  mają długości 12 i 6. Oblicz długość promienia okręgu stycznego do obu przyprostokątnych, którego środek
mają długości 12 i 6. Oblicz długość promienia okręgu stycznego do obu przyprostokątnych, którego środek  leży na przeciwprostokątnej, oraz oblicz odległości środka
leży na przeciwprostokątnej, oraz oblicz odległości środka 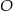 od wierzchołków trójkąta
od wierzchołków trójkąta 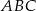 .
.
Ze zbioru 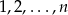 losujemy kolejno bez zwracania 2 liczby
losujemy kolejno bez zwracania 2 liczby 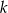 i
i 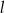 . Dla jakich wartości
. Dla jakich wartości  prawdopodobieństwo tego, że
prawdopodobieństwo tego, że 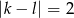 jest większe od
jest większe od 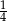 ?
?
