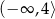Punkty 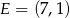 i
i 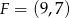 to środki boków, odpowiednio
to środki boków, odpowiednio 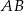 i
i 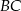 kwadratu
kwadratu 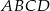 . Przekątna tego kwadratu ma długość
. Przekątna tego kwadratu ma długość
A) 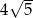 B) 10 C)
B) 10 C) 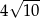 D) 20
D) 20
/Szkoła średnia
Punkty 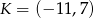 i
i 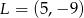 to środki boków, odpowiednio
to środki boków, odpowiednio 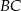 i
i 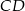 kwadratu
kwadratu 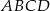 . Przekątna tego kwadratu ma długość
. Przekątna tego kwadratu ma długość
A) 32 B) 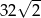 C)
C) 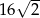 D) 16
D) 16
Oblicz 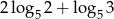 .
.
Oblicz 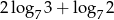 .
.
Dany jest trójkąt równoboczny 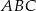 . Okrąg o średnicy
. Okrąg o średnicy 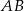 przecina bok
przecina bok 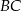 w punkcie
w punkcie 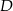 .
.
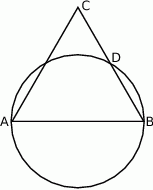
Wykaż, że 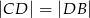 .
.
Dla każdej dodatniej liczby  iloraz
iloraz 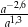 jest równy
jest równy
A) 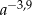 B)
B) 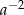 C)
C) 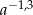 D)
D) 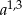
Dla każdej dodatniej liczby  iloraz
iloraz 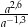 jest równy
jest równy
A) 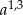 B)
B) 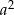 C)
C) 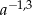 D)
D) 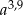
Każde z ramion trójkąta równoramiennego ma długość 20. Kąt zawarty między ramionami tego trójkąta ma miarę 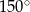 . Pole tego trójkąta jest równe
. Pole tego trójkąta jest równe
A) 100 B) 200 C) 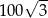 D)
D) 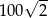
Każde z ramion trójkąta równoramiennego ma długość 20. Kąt zawarty między ramionami tego trójkąta ma miarę 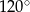 . Pole tego trójkąta jest równe
. Pole tego trójkąta jest równe
A) 100 B) 200 C) 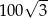 D)
D) 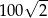
Pole powierzchni trójkąta równoramiennego o ramionach długości 6 cm i kącie między nimi 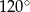 jest równe
jest równe
A) 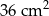 B)
B) 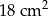 C)
C) 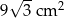 D)
D) 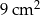
Ramię trójkąta równoramiennego  ma długość 8, a jeden z kątów tego trójkąta ma miarę
ma długość 8, a jeden z kątów tego trójkąta ma miarę 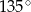 . Pole tego trójkąta jest równe
. Pole tego trójkąta jest równe
A) 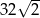 B)
B) 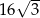 C) 32 D)
C) 32 D) 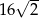
Wierzchołki trójkąta 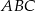 mają współrzędne
mają współrzędne 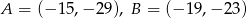 i
i 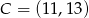 . Bok
. Bok 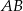 trójkąta
trójkąta 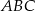 ma długość
ma długość
A) 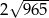 B)
B) 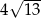 C)
C) 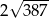 D)
D) 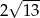
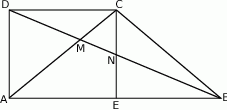
Punkt 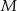 jest punktem wspólnym przekątnych trapezu prostokątnego
jest punktem wspólnym przekątnych trapezu prostokątnego 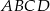 . Punkt
. Punkt 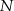 jest punktem wspólnym przekątnej
jest punktem wspólnym przekątnej 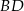 i wysokości
i wysokości 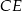 opuszczonej na dłuższą podstawę
opuszczonej na dłuższą podstawę 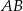 . Wykaż, że
. Wykaż, że 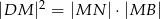 .
.
Funkcja
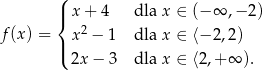
A) nie ma miejsc zerowych B) ma trzy miejsca zerowe
C) ma jedno miejsce zerowe D) ma dwa miejsca zerowe
Rozwiąż równanie 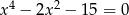 .
.
Funkcja 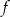 określona jest wzorem
określona jest wzorem
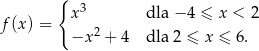
Prawdziwa jest nierówność
A) 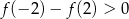 B)
B) 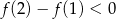
C) 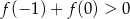 D)
D) 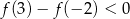
Funkcja 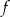 określona jest wzorem
określona jest wzorem
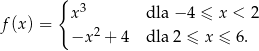
Prawdziwa jest nierówność
A) 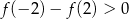 B)
B) 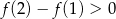
C) 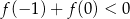 D)
D) 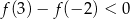
Funkcja 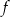 określona jest wzorem
określona jest wzorem
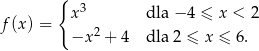
Prawdziwa jest nierówność
A) 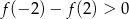 B)
B) 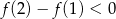
C) 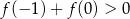 D)
D) 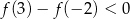
Udowodnij, że trzy środkowe rozcinają trójkąt na sześć części o równych polach.
Odcinki 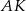 i
i 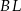 są wysokościami trójkąta ostrokątnego
są wysokościami trójkąta ostrokątnego 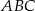 , a punkt
, a punkt 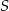 punktem ich przecięcia. Wykaż, że podobne są trójkąty:
punktem ich przecięcia. Wykaż, że podobne są trójkąty:
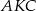 i
i 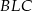 ;
; 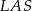 i
i 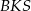 ;
; 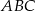 i
i 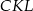 .
.
W prostokątnym układzie współrzędnych zaznacz zbiór tych wszystkich punktów płaszczyzny o współrzędnych 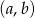 , dla których funkcja
, dla których funkcja 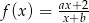 jest funkcją homograficzną, malejącą w każdym z przedziałów:
jest funkcją homograficzną, malejącą w każdym z przedziałów: 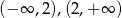 .
.
Dany jest ciąg arytmetyczny, w którym 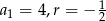 . Wtedy
. Wtedy
A) 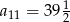 B)
B) 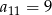 C)
C) 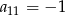 D)
D) 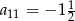
Odcinki 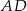 i
i 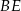 są wysokościami trójkąta ostrokątnego
są wysokościami trójkąta ostrokątnego 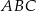 , a punkt
, a punkt 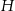 jest punktem ich przecięcia. Uzasadnij, że punkty
jest punktem ich przecięcia. Uzasadnij, że punkty 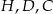 i
i 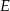 leżą na jednym okręgu.
leżą na jednym okręgu.
Dany jest zbiór wszystkich graniastosłupów prawidłowych sześciokątnych, których suma długości wszystkich krawędzi jest równa 216. Oblicz długość krawędzi podstawy i wysokość tego z danych graniastosłupów, który ma największe pole powierzchni bocznej.
Liczba 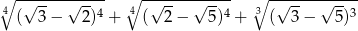 jest równa
jest równa
A) 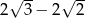 B)
B) 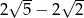 C)
C) 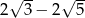 D)
D) 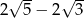
Liczba 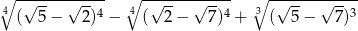 jest równa
jest równa
A) 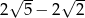 B)
B) 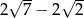 C)
C) 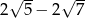 D)
D) 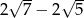
W ciągu arytmetycznym 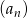 określonym dla
określonym dla 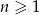 dane są
dane są 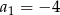 i
i 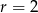 . Którym wyrazem tego ciągu jest liczba 156?
. Którym wyrazem tego ciągu jest liczba 156?
A) 81 B) 80 C) 76 D) 77
Na rysunku poniżej przedstawiono fragment wykresu funkcji kwadratowej 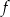 określonej wzorem
określonej wzorem 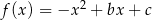 . Wierzchołek paraboli będącej wykresem tej funkcji ma współrzędne
. Wierzchołek paraboli będącej wykresem tej funkcji ma współrzędne 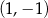 .
.
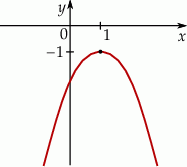
Stąd wynika, że:
A) 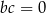 B)
B) 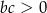 C)
C) 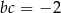 D)
D) 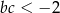
Zbiorem wartości funkcji kwadratowej 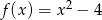 jest
jest
A) 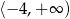 B)
B) 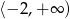 C)
C) 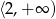 D)
D) 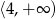
Zbiorem wartości funkcji kwadratowej 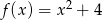 jest
jest
A) 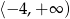 B)
B) 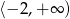 C)
C) 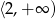 D)
D) 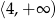
Funkcja 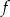 jest określona wzorem
jest określona wzorem 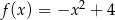 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Zbiorem wartości funkcji
. Zbiorem wartości funkcji 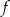 jest przedział
jest przedział
A) 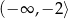 B)
B) 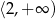 C)
C) 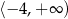 D)
D)