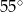Wartość wyrażenia 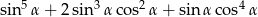 jest równa
jest równa
A) 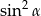 B)
B) 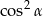 C)
C) 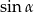 D)
D) 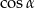
/Szkoła średnia
Wyrażenie 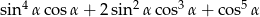 jest równe
jest równe
A) 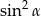 B)
B) 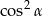 C)
C) 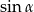 D)
D) 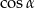
Wysokość rombu o boku długości 6 i kącie ostrym 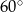 jest równa
jest równa
A) 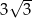 B) 3 C)
B) 3 C) 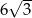 D) 6
D) 6
Wysokość rombu o boku długości 8 i kącie ostrym 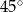 jest równa
jest równa
A) 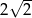 B) 4 C)
B) 4 C) 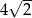 D) 8
D) 8
Rozwiąż nierówność
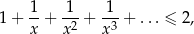
gdzie lewa strona jest sumą zbieżnego szeregu geometrycznego.
Dana jest funkcja 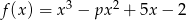 .
.
- Znajdź taką wartość
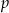 , dla której funkcja
, dla której funkcja 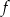 osiąga minimum w punkcie
osiąga minimum w punkcie 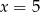 .
. - Dla wyznaczonego
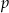 podaj przedziały monotoniczności funkcji
podaj przedziały monotoniczności funkcji 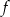 .
.
Do wykresu funkcji 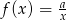 , dla
, dla 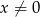 należy punkt
należy punkt 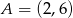 . Wtedy
. Wtedy
A) 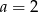 B)
B) 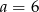 C)
C) 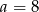 D)
D) 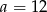
Do wykresu funkcji 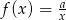 , dla
, dla 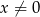 należy punkt
należy punkt 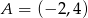 . Wtedy
. Wtedy
A) 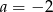 B)
B) 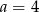 C)
C) 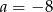 D)
D) 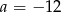
Funkcja 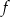 jest funkcją okresową o okresie podstawowym równym
jest funkcją okresową o okresie podstawowym równym 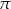 . W przedziale
. W przedziale 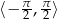 funkcja określona jest wzorem
funkcja określona jest wzorem
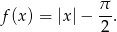
- Wyznacz miejsca zerowe funkcji
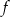 .
. - Podaj zbiór wartości funkcji
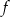 .
. - Oblicz
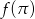 oraz
oraz 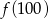 , przyjmując
, przyjmując 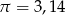 .
. - Naszkicuj wykres funkcji
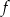 w przedziale
w przedziale 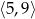 .
.
Prosta 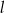 przecina okrąg o środku
przecina okrąg o środku 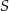 w punktach
w punktach 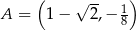 i
i 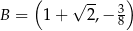 . Punkt
. Punkt 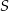 leży na prostej
leży na prostej 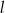 . Oblicz pole koła ograniczonego tym okręgiem.
. Oblicz pole koła ograniczonego tym okręgiem.
Suma cyfr liczby trzycyfrowej podzielnej przez 5 jest równa 17. Jeśli zapiszemy cyfry tej liczby w przeciwnej kolejności, to otrzymamy liczbę o 99 większą od początkowej. Wyznacz liczbę początkową.
Suma cyfr liczby trzycyfrowej podzielnej przez 5 jest równa 14. Jeśli zapiszemy cyfry tej liczby w przeciwnej kolejności, to otrzymamy liczbę o 198 większą od początkowej. Wyznacz liczbę początkową.
Suma cyfr liczby trzycyfrowej podzielnej przez 5 jest równa 15. Jeśli zapiszemy cyfry tej liczby w odwrotnej kolejności, to otrzymamy liczbę o 198 większą od początkowej. Wyznacz liczbę początkową.
Liczba 2 jest miejscem zerowym wielomianu 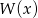 . Wyznacz resztę z dzielenia tego wielomianu przez wielomian
. Wyznacz resztę z dzielenia tego wielomianu przez wielomian 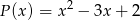 jeśli wiadomo, że w wyniku dzielenia wielomianu
jeśli wiadomo, że w wyniku dzielenia wielomianu 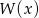 przez dwumian
przez dwumian 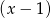 otrzymujemy resztę 5.
otrzymujemy resztę 5.
Udowodnij, że jeżeli 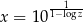 i
i 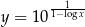 , to
, to 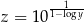 .
.
Wyznacz wszystkie całkowite wartości 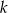 , dla których funkcja
, dla których funkcja 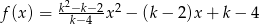 osiąga minimum i ma dwa różne miejsca zerowe.
osiąga minimum i ma dwa różne miejsca zerowe.
Dany jest równoległobok 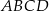 , w którym
, w którym 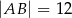 ,
, 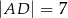 oraz
oraz
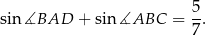
Oblicz pole równoległoboku 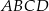 .
.
Liczba 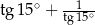 jest równa
jest równa
A) 4 B) 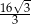 C) 1 D)
C) 1 D) 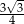
Liczba 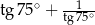 jest równa
jest równa
A) 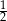 B)
B) 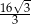 C) 4 D)
C) 4 D) 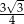
Liczby naturalne 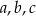 są większe od 1 oraz są kolejnymi wyrazami ciągu geometrycznego. Liczba
są większe od 1 oraz są kolejnymi wyrazami ciągu geometrycznego. Liczba  spełnia warunek
spełnia warunek
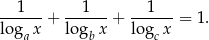
Wykaż, że  jest sześcianem liczby naturalnej.
jest sześcianem liczby naturalnej.
Samochód jadący autostradą pali 5,6 litra paliwa na 100km. Napisz wzór funkcji  określającej przebytą drogę (w kilometrach) w zależnosci od zużytego paliwa
określającej przebytą drogę (w kilometrach) w zależnosci od zużytego paliwa 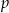 (w litrach).
(w litrach).
Liczba 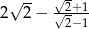 jest liczbą
jest liczbą
A) wymierną B) niewymierną C) większą niż 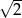 D) naturalną
D) naturalną
Liczba 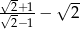 jest liczbą
jest liczbą
A) wymierną B) niewymierną C) mniejszą niż 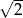 D) naturalną
D) naturalną
Udowodnij, że jeśli
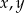 są liczbami rzeczywistymi, to
są liczbami rzeczywistymi, to 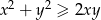 .
. 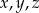 są liczbami rzeczywistymi takimi, że
są liczbami rzeczywistymi takimi, że 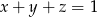 , to
, to 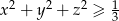 .
.
Dany jest sześciokąt foremny 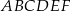 o polu równym
o polu równym 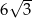 (zobacz rysunek).
(zobacz rysunek).
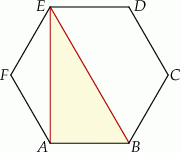
Pole trójkąta 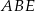 jest równe
jest równe
A) 6 B) 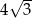 C)
C) 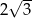 D) 4
D) 4
Dane są graniastosłup i ostrosłup o takich samych podstawach. Liczba wszystkich wierzchołków tego graniastosłupa jest o 9 większa od liczby wszystkich wierzchołków tego ostrosłupa. Podstawą każdej z tych brył jest
A) dziewięciokąt. B) ośmiokąt. C) osiemnastokąt. D) dziesięciokąt.
Dane są graniastosłup i ostrosłup o takich samych podstawach. Liczba wszystkich wierzchołków tego graniastosłupa jest o 10 większa od liczby wszystkich wierzchołków tego ostrosłupa. Podstawą każdej z tych brył jest
A) dziewięciokąt. B) ośmiokąt. C) jedenastokąt. D) dziesięciokąt.
Na trójkącie 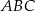 opisano okrąg i poprowadzono styczną do okręgu w punkcie
opisano okrąg i poprowadzono styczną do okręgu w punkcie 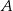 (zobacz rysunek obok).
(zobacz rysunek obok).
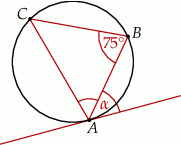
Jeżeli 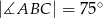 i kąt dopisany
i kąt dopisany  jest równy
jest równy 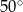 , to kąt
, to kąt 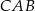 ma miarę:
ma miarę:
A) 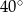 B)
B) 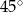 C)
C) 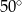 D)
D)