Wyznacz wszystkie liczby całkowite 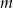 , dla których równanie
, dla których równanie
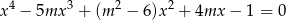
nie ma rozwiązań wymiernych.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Wyznacz wszystkie liczby całkowite 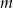 , dla których równanie
, dla których równanie
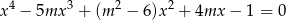
nie ma rozwiązań wymiernych.
Rozwiąż równanie 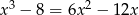 .
.
Rozwiąż równanie 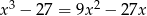 .
.
Rozwiąż równanie 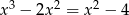 .
.
Dany jest wielomian 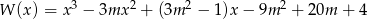 . Wykres tego wielomianu, po przesunięciu o wektor
. Wykres tego wielomianu, po przesunięciu o wektor ![→ u = [− 3,0]](https://img.zadania.info/zad/8700545/HzadT1x.gif) , przechodzi przez początek układu współrzędnych. Wyznacz wszystkie pierwiastki wielomianu
, przechodzi przez początek układu współrzędnych. Wyznacz wszystkie pierwiastki wielomianu  .
.
Dane są liczby 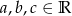 takie, że równanie
takie, że równanie 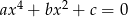 ma cztery rozwiązania rzeczywiste
ma cztery rozwiązania rzeczywiste 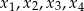 . Oblicz wartość wyrażenia
. Oblicz wartość wyrażenia 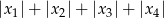 .
.
Wyznacz wielomian czwartego stopnia 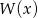 wiedząc, że liczba 3 jest jego czterokrotnym pierwiastkiem oraz
wiedząc, że liczba 3 jest jego czterokrotnym pierwiastkiem oraz 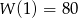 .
.
Rozwiąż równanie 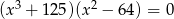 .
.
Rozwiąż równanie 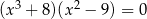 .
.
Rozwiąż równanie 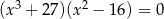 .
.
Rozwiąż równanie 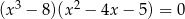 .
.
Rozwiąż równanie 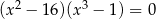 .
.
Rozwiąż równanie 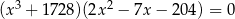 .
.
Rozwiąż równanie 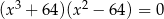 .
.
Zbadaj, dla jakich wartości parametru 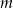 równanie
równanie 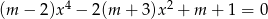 ma cztery różne pierwiastki rzeczywiste.
ma cztery różne pierwiastki rzeczywiste.
Dana jest funkcja 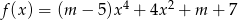 , gdzie
, gdzie 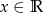 . Wyznacz wszystkie wartości parametru
. Wyznacz wszystkie wartości parametru 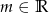 , dla których funkcja ma 4 różne miejsca zerowe.
, dla których funkcja ma 4 różne miejsca zerowe.
Suma wszystkich czterech współczynników wielomianu 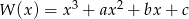 jest równa 0. Trzy pierwiastki tego wielomianu tworzą ciąg arytmetyczny o różnicy równej 3. Oblicz współczynniki
jest równa 0. Trzy pierwiastki tego wielomianu tworzą ciąg arytmetyczny o różnicy równej 3. Oblicz współczynniki 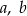 i
i  . Rozważ wszystkie możliwe przypadki.
. Rozważ wszystkie możliwe przypadki.
Współczynniki wielomianu 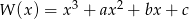 spełniają warunek:
spełniają warunek: 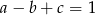 . Trzy pierwiastki tego wielomianu tworzą ciąg arytmetyczny o różnicy równej 3. Oblicz współczynniki
. Trzy pierwiastki tego wielomianu tworzą ciąg arytmetyczny o różnicy równej 3. Oblicz współczynniki 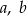 i
i  . Rozważ wszystkie możliwe przypadki.
. Rozważ wszystkie możliwe przypadki.
Wielomian 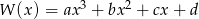 , gdzie
, gdzie 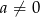 , ma dwa różne miejsca zerowe:
, ma dwa różne miejsca zerowe: 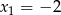 oraz
oraz 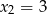 , przy czym pierwiastek
, przy czym pierwiastek 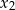 jest dwukrotny. Dla argumentu 1 wartość wielomianu jest równa
jest dwukrotny. Dla argumentu 1 wartość wielomianu jest równa 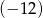 .
.
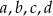 .
. 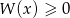 .
.Dany jest wielomian 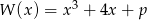 , gdzie
, gdzie 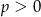 jest liczbą pierwszą. Znajdź
jest liczbą pierwszą. Znajdź 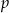 wiedząc, że
wiedząc, że 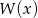 ma pierwiastek całkowity.
ma pierwiastek całkowity.
Pierwiastkami wielomianu 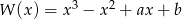 są tylko dwie liczby: 2 oraz (-3).
są tylko dwie liczby: 2 oraz (-3).
 i
i 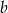 .
. Liczby 2 i 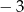 są pierwiastkami wielomianu
są pierwiastkami wielomianu 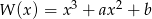 . Wyznacz liczby
. Wyznacz liczby  i
i 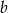 oraz trzeci pierwiastek wielomianu.
oraz trzeci pierwiastek wielomianu.
Liczby 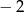 i 3 są pierwiastkami wielomianu
i 3 są pierwiastkami wielomianu 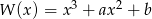 . Wyznacz liczby
. Wyznacz liczby  i
i 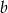 oraz trzeci pierwiastek wielomianu.
oraz trzeci pierwiastek wielomianu.
Wielomian 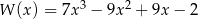 ma dokładnie jeden pierwiastek rzeczywisty. Oblicz ten pierwiastek.
ma dokładnie jeden pierwiastek rzeczywisty. Oblicz ten pierwiastek.
Wiedząc, że liczba 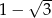 jest pierwiastkiem wielomianu
jest pierwiastkiem wielomianu 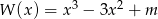 , wyznacz wartość parametru
, wyznacz wartość parametru 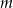 .
.
Wykaż, że dla dowolnej wartości parametru  równanie
równanie
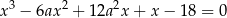
ma dokładnie jedno rozwiązanie rzeczywiste.
Rozwiąż równanie 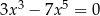 .
.
Rozwiąż równanie 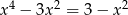 .
.
Rozwiąż równanie 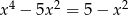 .
.
Rozwiąż równanie 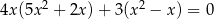 .
.
Miejscem zerowym wielomianu 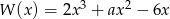 jest liczba
jest liczba 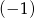 .
.
 .
. 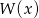 .
.Dla jakich wartości parametru 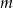 równanie
równanie ![3 2 2 (x + 3x − 4)[(m − 5 )x + (m − 2)x − 1 ] = 0](https://img.zadania.info/zad/9801521/HzadT1x.gif) ma cztery różne pierwiastki?
ma cztery różne pierwiastki?
Oblicz sumę kwadratów pierwiastków równania 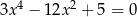 .
.
