Jednym z pierwiastków wielomianu 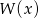 stopnia trzeciego jest liczba 1, a suma pozostałych dwóch pierwiastków jest równa 0. Do wykresu tego wielomianu należy punkt
stopnia trzeciego jest liczba 1, a suma pozostałych dwóch pierwiastków jest równa 0. Do wykresu tego wielomianu należy punkt 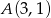 . Wiedząc, że reszta z dzielenia wielomianu
. Wiedząc, że reszta z dzielenia wielomianu 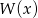 przez dwumian
przez dwumian 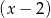 jest równa
jest równa 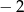 , wyznacz wzór tego wielomianu.
, wyznacz wzór tego wielomianu.
/Szkoła średnia/Równania/Wielomianowe
Rozwiąż równanie 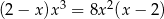 .
.
Rozwiąż równanie 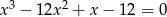 .
.
Rozwiąż równanie 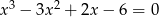 .
.
Rozwiąż równanie 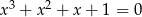 .
.
Rozwiąż równanie 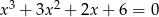 .
.
Rozwiąż równanie 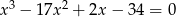 .
.
Rozwiąż równanie 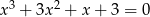 .
.
Rozwiąż równanie 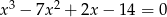 .
.
Rozwiąż równanie 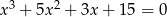 .
.
Rozwiąż równanie 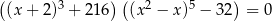 .
.
Pierwiastki równania 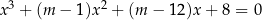 z niewiadomą
z niewiadomą  tworzą trzywyrazowy ciąg geometryczny. Oblicz
tworzą trzywyrazowy ciąg geometryczny. Oblicz 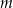 oraz sumę kwadratów tych pierwiastków.
oraz sumę kwadratów tych pierwiastków.
Dane są liczby wymierne 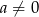 i
i 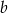 takie, że równanie
takie, że równanie 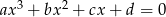 ma dwa pierwiastki wymierne. Wykaż, że
ma dwa pierwiastki wymierne. Wykaż, że  i
i 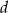 są liczbami wymiernymi.
są liczbami wymiernymi.
Dany jest wielomian 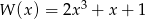
- Uzasadnij, że wielomian
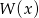 nie ma dodatnich pierwiastków.
nie ma dodatnich pierwiastków. - Uzasadnij, że wielomian
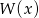 nie ma pierwiastków wymiernych.
nie ma pierwiastków wymiernych. - Uzasadnij, że wielomian
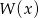 ma co najmniej jeden pierwiastek.
ma co najmniej jeden pierwiastek.
Wiedząc, że wielomian 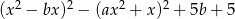 jest wielomianem stopnia 3 oraz 1 jest jego pierwiastkiem wyznacz
jest wielomianem stopnia 3 oraz 1 jest jego pierwiastkiem wyznacz  i
i 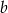 .
.
Wykaż, że równanie 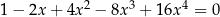 nie ma rozwiązań rzeczywistych.
nie ma rozwiązań rzeczywistych.
Znajdź wszystkie wartości parametru 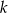 , dla których równanie
, dla których równanie 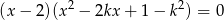 ma więcej niż jeden pierwiastek.
ma więcej niż jeden pierwiastek.
Wielomian 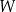 jest określony wzorem
jest określony wzorem 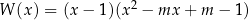 dla każdego
dla każdego 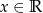 . Wyznacz wszystkie wartości parametru
. Wyznacz wszystkie wartości parametru 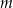 , dla których wielomian
, dla których wielomian 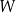 ma dokładnie jeden pierwiastek rzeczywisty.
ma dokładnie jeden pierwiastek rzeczywisty.
Rozwiąż równanie 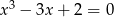 .
.
Rozwiąż równanie 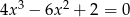 .
.
Rozwiąż równanie 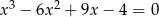 .
.
Wyznacz wszystkie wartości parametru 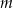 , dla których równanie
, dla których równanie
![2 2 (x − 4 )[x + (m − 3)x + m − m − 6] = 0](https://img.zadania.info/zad/7940380/HzadT1x.gif)
ma trzy różne rozwiązania rzeczywiste 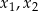 oraz
oraz 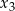 , spełniające warunek
, spełniające warunek
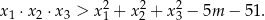
Dane jest równanie
![2 (x − 2 )⋅[(m − 7)x + 2(m + 3 )x− (2m + 3)] = 0](https://img.zadania.info/zad/8155916/HzadT0x.gif)
z niewiadomą  i parametrem
i parametrem 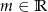 . Wyznacz wszystkie wartości parametru
. Wyznacz wszystkie wartości parametru 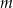 , dla których to równanie ma trzy różne rozwiązania rzeczywiste tego samego znaku.
, dla których to równanie ma trzy różne rozwiązania rzeczywiste tego samego znaku.
Wyznacz wszystkie wartości parametru 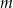 , dla których równanie
, dla których równanie
![2 2 (x − 3)[x + (m − 9)x + m − m + 16] = 0](https://img.zadania.info/zad/6498821/HzadT1x.gif)
ma trzy różne rozwiązania rzeczywiste 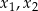 oraz
oraz 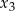 , spełniające warunek
, spełniające warunek
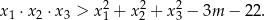
Dane jest równanie
![2 (x − 6) ⋅[(m − 2)x − 4(m + 3)x + m + 1] = 0](https://img.zadania.info/zad/4031216/HzadT0x.gif)
z niewiadomą  i parametrem
i parametrem 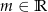 . Wyznacz wszystkie wartości parametru
. Wyznacz wszystkie wartości parametru 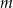 , dla których to równanie ma trzy różne rozwiązania rzeczywiste tego samego znaku.
, dla których to równanie ma trzy różne rozwiązania rzeczywiste tego samego znaku.
Liczby 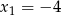 i
i 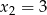 są pierwiastkami wielomianu
są pierwiastkami wielomianu 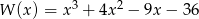 . Oblicz trzeci pierwiastek tego wielomianu.
. Oblicz trzeci pierwiastek tego wielomianu.
Uzasadnij, że wielomian 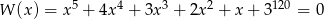 nie ma pierwiastków wymiernych.
nie ma pierwiastków wymiernych.
Dla jakich wartości parametru 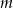 zbiór rozwiązań równania
zbiór rozwiązań równania 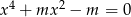 jest dwuelementowy?
jest dwuelementowy?
Wyznacz wartość parametru 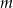 , dla którego równanie
, dla którego równanie
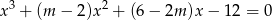
ma trzy pierwiastki 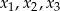 spełniające warunki
spełniające warunki 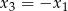 oraz
oraz 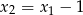 .
.
Wykaż, że jeżeli pierwiastkiem wielomianu
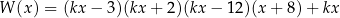
jest liczba całkowita podzielna przez 5, to 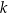 nie jest liczbą całkowitą.
nie jest liczbą całkowitą.
Rozwiąż równanie 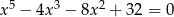 .
.
Rozwiąż równanie 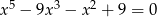 .
.
Wykaż, że równanie 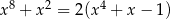 ma tylko jedno rozwiązanie rzeczywiste
ma tylko jedno rozwiązanie rzeczywiste 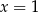 .
.
Wykaż, że równanie 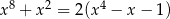 ma tylko jedno rozwiązanie rzeczywiste
ma tylko jedno rozwiązanie rzeczywiste 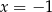 .
.
Rozwiąż równanie 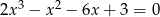 .
.
Rozwiąż równanie 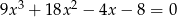 .
.
Wyznacz pierwiastki wielomianu 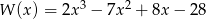 .
.
Rozwiąż równanie 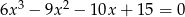 .
.
Rozwiąż równanie 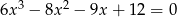 .
.
Rozwiąż równanie 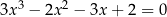 .
.
Rozwiąż równanie 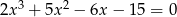 .
.
Rozwiąż równanie 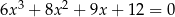 .
.
Rozwiąż równanie 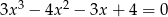 .
.
Rozwiąż równanie
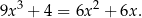
Rozwiąż równanie
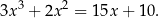
Rozwiąż równanie
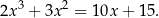
Rozwiąż równanie 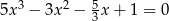 .
.
Rozwiąż równanie 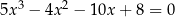 .
.
Rozwiąż równanie 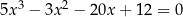 .
.
Rozwiąż równanie 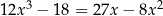 .
.
Rozwiąż równanie 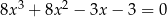 .
.
Rozwiąż równanie 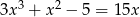 .
.
Rozwiąż równanie 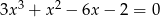 .
.
Rozwiąż równanie 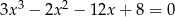 .
.
Rozwiąż równanie 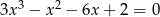 .
.
Rozwiąż równanie 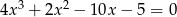 .
.
Rozwiąż równanie 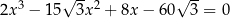 .
.

