Dany jest wielomian 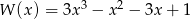 .
.
- Rozłóż wielomian na czynniki liniowe.
- Rozwiąż nierówność
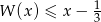 .
.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Dany jest wielomian 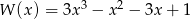 .
.
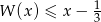 .
.Dany jest wielomian 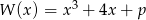 , gdzie
, gdzie 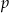 jest liczbą pierwszą. Wyznacz
jest liczbą pierwszą. Wyznacz 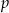 wiedząc, że
wiedząc, że 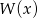 ma pierwiastek całkowity.
ma pierwiastek całkowity.
Wyznacz wszystkie całkowite wartości parametru 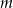 , dla których równanie
, dla których równanie
![3 2 [ 2 2 ] (x + 2x + 2x + 1 ) x − (2m + 1)x + m + m = 0](https://img.zadania.info/zad/5455135/HzadT1x.gif)
ma trzy, parami różne, pierwiastki rzeczywiste, takie że jeden z nich jest średnią arytmetyczną dwóch pozostałych.
Wyznacz wszystkie wartości parametru 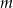 , dla których równanie
, dla których równanie
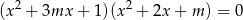
ma cztery różne pierwiastki, których suma sześcianów jest równa 4.
Rozwiąż równanie 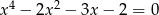 .
.
Wykaż, że jeżeli wielomian 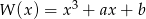 ma pierwiastek dwukrotny, to
ma pierwiastek dwukrotny, to 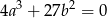 .
.
Wyznacz te wartości parametru 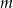 , dla których równanie
, dla których równanie 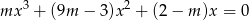 ma co najmniej jedno rozwiązanie dodatnie.
ma co najmniej jedno rozwiązanie dodatnie.
Dobierz wartości 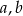 i
i  tak, aby liczby
tak, aby liczby 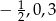 były pierwiastkami wielomianu
były pierwiastkami wielomianu 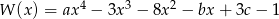 .
.
Znajdź te wartości parametru 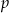 , dla których równanie
, dla których równanie 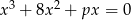 ma trzy różne rozwiązania.
ma trzy różne rozwiązania.
Pierwiastki wielomianu 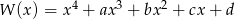 tworzą czterowyrazowy ciąg arytmetyczny o sumie wyrazów równej zero. Wiadomo ponadto, że
tworzą czterowyrazowy ciąg arytmetyczny o sumie wyrazów równej zero. Wiadomo ponadto, że 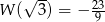 . Oblicz współczynniki
. Oblicz współczynniki 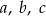 i
i 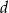 . Rozważ wszystkie możliwe przypadki.
. Rozważ wszystkie możliwe przypadki.
Dane jest równanie ![2 2 (x + 3)[x + (p + 4)x + (p + 1 ) ] = 0](https://img.zadania.info/zad/6258301/HzadT0x.gif) z niewiadomą
z niewiadomą  .
.
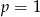 .
. 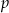 , dla których równanie to ma tylko jedno rozwiązanie.
, dla których równanie to ma tylko jedno rozwiązanie.Wyznacz te wartości parametru 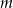 , dla których równanie
, dla których równanie
![2 2 (x− 3)[x − 2(2m + 1 )x+ (m + 2) ] = 0](https://img.zadania.info/zad/8529863/HzadT1x.gif)
ma trzy różne rozwiązania.
Wyznacz wszystkie wartości parametru 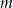 , dla których równanie
, dla których równanie
![2 2 (x+ 2)[x − (m + 1)x − 6m + 3m )] = 0](https://img.zadania.info/zad/2956182/HzadT1x.gif)
ma dokładnie dwa rozwiązania.
Wyznacz wszystkie wartości parametru 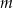 , dla których równanie
, dla których równanie
![2 2 (x− 3)[x + (m − 1)x − 6m + 2m )] = 0](https://img.zadania.info/zad/1637258/HzadT1x.gif)
ma dokładnie dwa rozwiązania.
Rozwiąż równanie 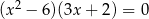 .
.
Rozwiąż równanie 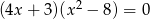 .
.
Wykaż, że równanie 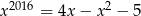 nie ma rozwiązań rzeczywistych.
nie ma rozwiązań rzeczywistych.
Określ liczbę pierwiastków równania 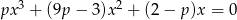 w zależności od wartości parametru
w zależności od wartości parametru 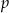 . Naszkicuj wykres funkcji, która każdej wartości parametru
. Naszkicuj wykres funkcji, która każdej wartości parametru 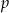 przyporządkowuje liczbę pierwiastków tego równania.
przyporządkowuje liczbę pierwiastków tego równania.
Wyznacz wartości parametrów  i
i 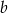 dla których jedynymi rozwiązaniami równania
dla których jedynymi rozwiązaniami równania
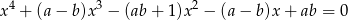
są liczby 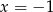 i
i 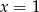 .
.
Liczba  jest pierwiastkiem wielomianu
jest pierwiastkiem wielomianu 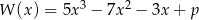 . Wyznacz pozostałe pierwiastki tego wielomianu i rozwiąż nierówność
. Wyznacz pozostałe pierwiastki tego wielomianu i rozwiąż nierówność 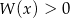 .
.
Wielomian 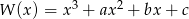 ma trzy pierwiastki rzeczywiste, które tworzą ciąg arytmetyczny o różnicy
ma trzy pierwiastki rzeczywiste, które tworzą ciąg arytmetyczny o różnicy 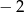 . Oblicz współczynniki
. Oblicz współczynniki 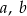 i
i  wiedząc, że
wiedząc, że 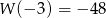 .
.
Rozwiąż równanie 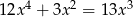 .
.
Wyznacz wszystkie wartości parametru 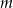 , dla których równanie
, dla których równanie 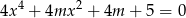 ma cztery różne pierwiastki rzeczywiste spełniające warunek
ma cztery różne pierwiastki rzeczywiste spełniające warunek
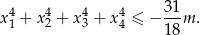
Rozwiąż równanie 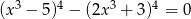 .
.
