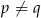Jeśli 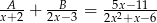 , to suma
, to suma 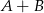 jest równa
jest równa
A) 0 B) 2 C) 1 D) 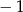
/Szkoła średnia/Zadania testowe/Liczby/Wyrażenia algebraiczne/Wymierne
Suma liczby odwrotnej do 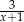 i przeciwnej do
i przeciwnej do 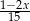 jest równa
jest równa
A) 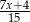 B)
B) 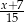 C)
C) 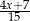 D)
D) 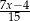
Wyrażenie wymierne 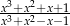 po uproszczeniu ma postać:
po uproszczeniu ma postać:
A) 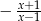 B)
B) 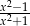 C)
C) 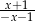 D)
D) 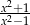
Wyrażenie wymierne 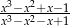 po uproszczeniu ma postać:
po uproszczeniu ma postać:
A) 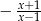 B)
B) 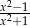 C)
C) 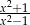 D)
D) 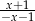
Po wykonaniu działań w wyrażeniu 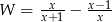 otrzymujemy
otrzymujemy
A) 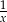 B)
B) 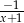 C)
C) 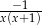 D)
D) 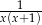
Wyrażenie 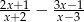 jest równe
jest równe
A) 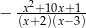 B)
B) 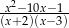 C)
C) 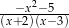 D)
D) 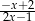
Wyrażenie 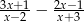 jest równe
jest równe
A) 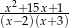 B)
B) 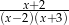 C)
C) 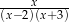 D)
D) 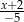
Po wykonaniu działania 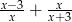 otrzymujemy
otrzymujemy
A) 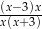 B)
B) 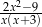 C)
C) 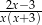 D)
D) 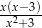
Wyrażenie 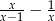 , określone dla
, określone dla 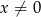 i
i 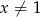 , jest równe
, jest równe
A) 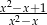 B)
B) 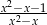 C)
C) 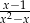 D)
D) 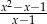
Po wykonaniu działań w wyrażeniu 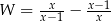 otrzymujemy
otrzymujemy
A) 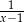 B)
B) 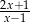 C)
C) 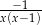 D)
D) 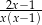
Wyrażenie 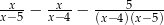 można zapisać w postaci
można zapisać w postaci
A) 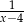 B)
B) 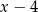 C)
C) 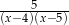 D)
D) 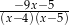
Potęga 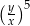 (gdzie
(gdzie  i
i 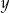 są różne od zera) jest równa
są różne od zera) jest równa
A) 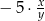 B)
B) 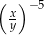 C)
C) 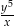 D)
D) 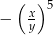
Po skróceniu wyrażenia 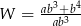 otrzymamy
otrzymamy
A) 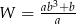 B)
B) 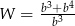 C)
C) 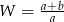 D)
D) 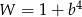
Po skróceniu wyrażenia 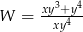 otrzymamy
otrzymamy
A) 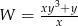 B)
B) 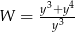 C)
C) 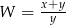 D)
D) 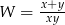
Po skróceniu wyrażenia 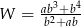 otrzymamy
otrzymamy
A) 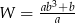 B)
B) 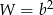 C)
C) 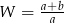 D)
D) 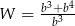
Wiadomo, że 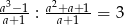 . Zatem
. Zatem 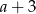 jest równe
jest równe
A) 7 B) 1 C) -1 D) 5
Wiadomo, że 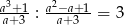 . Zatem
. Zatem 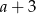 jest równe
jest równe
A) 7 B) 1 C) -1 D) 5
Wiadomo, że 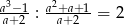 . Zatem
. Zatem 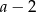 jest równe
jest równe
A) 7 B) 1 C) -1 D) 5
Liczba rzeczywista  spełnia warunek:
spełnia warunek: 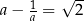 . Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Wartość wyrażenia 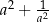 jest liczbą całkowitą. jest liczbą całkowitą. | P | F |
Liczba  jest liczbą wymierną. jest liczbą wymierną. | P | F |
Wyrażenie 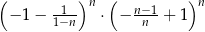 jest równe wyrażeniu
jest równe wyrażeniu
A) 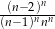 B)
B) 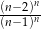 C)
C) 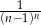 D)
D) 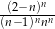
Dla każdej liczby rzeczywistej  różnej od
różnej od 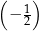 ,
,  , 0 i
, 0 i 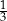 wartość wyrażenia
wartość wyrażenia
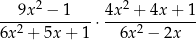
jest równa wartości wyrażenia
A) 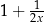 B)
B) 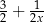 C)
C) 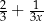 D)
D) 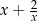
Dla każdej liczby rzeczywistej  , wyrażenie
, wyrażenie 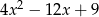 jest równe
jest równe
A) 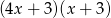 B)
B) 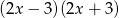 C)
C) 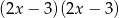 D)
D) 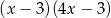
Dla każdej liczby rzeczywistej  , wyrażenie
, wyrażenie 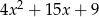 jest równe
jest równe
A) 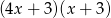 B)
B) 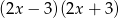 C)
C) 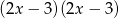 D)
D) 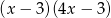
Jeśli 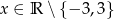 , to wyrażenie
, to wyrażenie 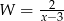 jest równoważne wyrażeniu
jest równoważne wyrażeniu
A) 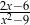 B)
B) 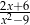 C)
C) 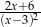 D)
D) 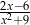
Jeśli 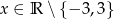 , to wyrażenie
, to wyrażenie 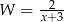 jest równoważne wyrażeniu
jest równoważne wyrażeniu
A) 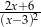 B)
B) 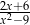 C)
C) 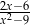 D)
D) 
Jeśli 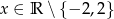 , to wyrażenie
, to wyrażenie 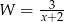 jest równoważne wyrażeniu
jest równoważne wyrażeniu
A) 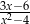 B)
B) 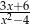 C)
C) 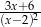 D)
D) 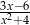
Dla każdej liczby rzeczywistej  różnej od 0 i 2 wyrażenie
różnej od 0 i 2 wyrażenie 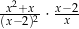 jest równe
jest równe
A) 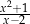 B)
B) 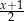 C)
C) 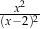 D)
D) 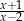
Dla każdej liczby rzeczywistej  różnej od 0 i
różnej od 0 i 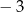 wyrażenie
wyrażenie 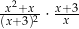 jest równe
jest równe
A) 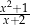 B)
B) 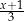 C)
C) 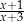 D)
D) 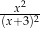
Dla każdej liczby rzeczywistej  różnej od
różnej od 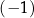 , 0 i 1, wartość wyrażenia
, 0 i 1, wartość wyrażenia 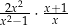 jest równa wartości wyrażenia
jest równa wartości wyrażenia
A) 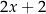 B)
B) 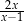 C)
C) 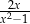 D)
D) 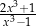
Po skróceniu wyrażenie 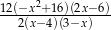 ma postać
ma postać
A) 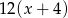 B)
B) 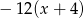 C)
C) 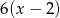 D) 6
D) 6
Dla każdej liczby rzeczywistej  różnej od
różnej od 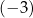 i
i 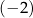 wartość wyrażenia
wartość wyrażenia
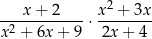
jest równa wartości wyrażenia
A) 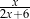 B)
B) 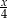 C)
C) 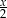 D)
D) 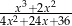
Wyrażenie 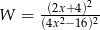 po skróceniu ma postać
po skróceniu ma postać
A) 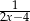 B)
B) 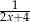 C)
C) 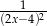 D)
D) 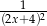
Dla każdej liczby rzeczywistej  różnej od
różnej od 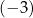 i
i 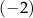 wartość wyrażenia
wartość wyrażenia
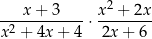
jest równa wartości wyrażenia
A) 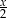 B)
B) 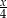 C)
C) 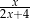 D)
D) 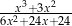
Dany jest wzór opisujący pole trapezu: 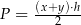 , gdzie
, gdzie  i
i 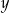 oznaczają długości podstaw trapezu, a
oznaczają długości podstaw trapezu, a 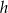 oznacza wysokość trapezu. Którym równaniem opisano
oznacza wysokość trapezu. Którym równaniem opisano  wyznaczone poprawnie z tego wzoru?
wyznaczone poprawnie z tego wzoru?
A) 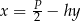 B)
B) 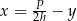 C)
C) 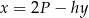 D)
D) 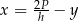
Jeżeli 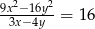 , to
, to
A) 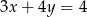 B)
B) 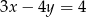 C)
C) 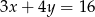 D)
D) 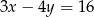
Jeżeli 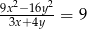 , to
, to
A) 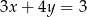 B)
B) 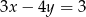 C)
C) 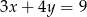 D)
D) 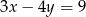
Jeżeli 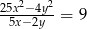 , to
, to
A) 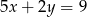 B)
B) 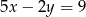 C)
C) 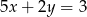 D)
D) 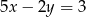
Jeśli 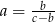 , to
, to
A) 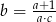 B)
B) 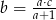 C)
C) 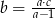 D)
D) 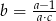
Jeśli 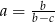 , to
, to
A) 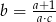 B)
B) 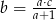 C)
C) 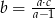 D)
D) 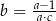
Dla każdej liczby rzeczywistej  , wyrażenie
, wyrażenie 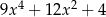 jest równe
jest równe
A) 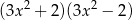 B)
B) 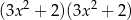
C) 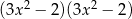 D)
D) 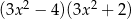
Jeżeli 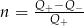 i
i 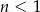 to
to
A) 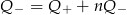 B)
B) 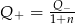 C)
C) 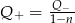 D)
D) 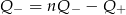
Jeżeli 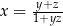 i
i 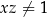 , to
, to
A) 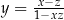 B)
B) 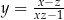 C)
C) 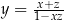 D)
D) 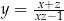
Jeżeli 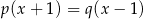 to
to
A) 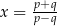 , gdy
, gdy 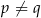 B)
B) 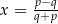 , gdy
, gdy 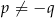
C) 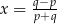 , gdy
, gdy 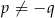 D)
D) 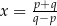 , gdy
, gdy 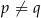
Jeżeli 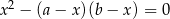 to
to
A) 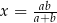 , gdy
, gdy 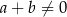 B)
B) 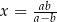 , gdy
, gdy 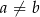
C) 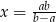 , gdy
, gdy 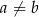 D)
D) 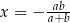 , gdy
, gdy