Uzasadnij, że dla każdej liczby 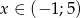 wyrażenie
wyrażenie 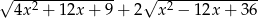 ma stałą wartość.
ma stałą wartość.
/Szkoła średnia/Liczby/Wyrażenia algebraiczne/Udowodnij.../1 literka
Wykaż, że jeżeli  jest parzystą liczbą całkowitą dodatnią, to liczba
jest parzystą liczbą całkowitą dodatnią, to liczba 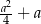 nie jest kwadratem liczby całkowitej.
nie jest kwadratem liczby całkowitej.
Wykaż, że dla 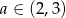 zachodzi równość
zachodzi równość 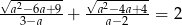 .
.
Udowodnij, że jeżeli liczba 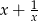 jest liczbą całkowitą, to liczba
jest liczbą całkowitą, to liczba 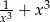 jest też liczbą całkowitą.
jest też liczbą całkowitą.
Wykaż, że liczba  jest dla dowolnej liczby naturalnej
jest dla dowolnej liczby naturalnej  kwadratem liczby całkowitej.
kwadratem liczby całkowitej.
Wiadomo, że 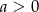 i
i 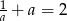 . Wykaż, że
. Wykaż, że 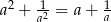 .
.
Ukryj
Podobne zadania
Uzasadnij, że jeżeli  jest liczbą rzeczywistą różną od zera i
jest liczbą rzeczywistą różną od zera i 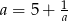 , to
, to 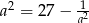 .
.
Uzasadnij, że jeżeli  jest liczbą rzeczywistą różną od zera i
jest liczbą rzeczywistą różną od zera i 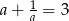 , to
, to 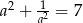 .
.
Uzasadnij, że dla dowolnej liczby naturalnej 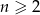 spełniona jest równość
spełniona jest równość
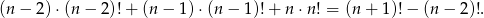
Udowodnij, że 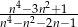 , dla
, dla 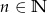 i
i 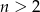 jest ułamkiem właściwym.
jest ułamkiem właściwym.
Wiadomo, że 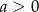 i
i 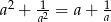 . Wykaż, że
. Wykaż, że 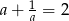 .
.

