Poniżej zamieszczono fragment tabeli wartości funkcji liniowej
 | 1 | 2 | 4 |
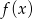 | 4 | 1 |
W pustym miejscu w tabeli powinna znajdować się liczba:
A) 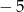 B) 5 C)
B) 5 C) 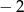 D) 2
D) 2
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Poniżej zamieszczono fragment tabeli wartości funkcji liniowej
 | 1 | 2 | 4 |
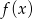 | 4 | 1 |
W pustym miejscu w tabeli powinna znajdować się liczba:
A) 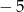 B) 5 C)
B) 5 C) 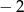 D) 2
D) 2
Funkcja liniowa 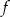 jest określona wzorem
jest określona wzorem 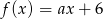 , gdzie
, gdzie 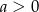 . Wówczas spełniony jest warunek
. Wówczas spełniony jest warunek
A) 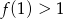 B)
B) 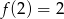 C)
C) 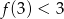 D)
D) 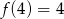
Funkcja liniowa 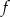 jest określona wzorem
jest określona wzorem 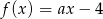 , gdzie
, gdzie 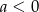 . Wówczas spełniony jest warunek
. Wówczas spełniony jest warunek
A) 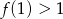 B)
B) 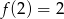 C)
C) 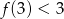 D)
D) 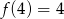
Funkcja liniowa 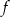 jest określona wzorem
jest określona wzorem 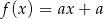 , gdzie
, gdzie 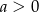 . Wówczas spełniony jest warunek
. Wówczas spełniony jest warunek
A) 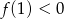 B)
B) 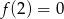 C)
C) 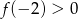 D)
D) 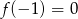
Funkcja liniowa 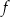 jest określona wzorem
jest określona wzorem 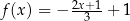 . Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Punkt przecięcia wykresu funkcji 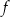 z prostą z prostą 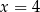 ma współrzędne ma współrzędne 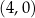 . . | P | F |
Punkt przecięcia wykresu funkcji 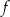 z prostą z prostą 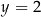 ma współrzędne ma współrzędne 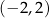 . . | P | F |
Funkcja 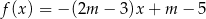 przyjmuje wartość
przyjmuje wartość 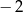 dla argumentu równego
dla argumentu równego 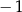 .
.
A) 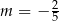 B)
B) 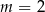 C)
C) 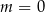 D)
D) 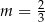
Argument funkcji 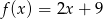 wzrasta o 5. Wówczas wartość funkcji wzrasta o
wzrasta o 5. Wówczas wartość funkcji wzrasta o
A) 4 B) 24 C) 10 D) 14
Jeżeli argument funkcji 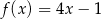 wzrośnie o 5, to wartość funkcji wzrośnie o
wzrośnie o 5, to wartość funkcji wzrośnie o
A) 18 B) 19 C) 20 D) 21
Argument funkcji 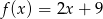 wzrasta o 7. Wówczas wartość funkcji wzrasta o
wzrasta o 7. Wówczas wartość funkcji wzrasta o
A) 7 B) 23 C) 9 D) 14
Argument funkcji 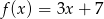 wzrasta o 2. Wówczas wartość funkcji wzrasta o
wzrasta o 2. Wówczas wartość funkcji wzrasta o
A) 4 B) 6 C) 10 D) 5
Funkcja liniowa 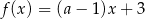 osiąga wartość najmniejszą równą 3. Wtedy
osiąga wartość najmniejszą równą 3. Wtedy
A) 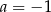 B)
B) 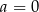 C)
C) 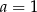 D)
D) 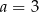
Funkcja liniowa 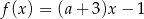 osiąga wartość największą równą
osiąga wartość największą równą 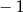 . Wtedy
. Wtedy
A) 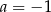 B)
B) 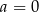 C)
C) 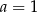 D)
D) 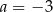
Funkcja liniowa 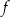 jest określona wzorem
jest określona wzorem 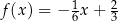 . Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Miejscem zerowym funkcji 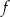 jest liczba 4. jest liczba 4. | P | F |
Punkt przecięcia wykresu funkcji 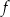 z osią z osią 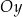 ma współrzędne ma współrzędne 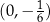 . . | P | F |
Funkcja liniowa 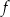 jest określona wzorem
jest określona wzorem 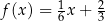 . Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Miejscem zerowym funkcji 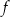 jest liczba jest liczba 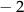 . . | P | F |
Punkt przecięcia wykresu funkcji 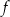 z osią z osią 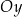 ma współrzędne ma współrzędne 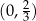 . . | P | F |
Funkcja 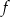 jest określona wzorem
jest określona wzorem 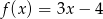 dla każdej liczby z przedziału
dla każdej liczby z przedziału 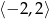 . Zbiorem wartości tej funkcji jest przedział
. Zbiorem wartości tej funkcji jest przedział
A) 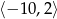 B)
B) 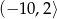 C)
C) 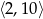 D)
D) 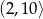
Funkcja 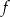 jest określona wzorem
jest określona wzorem 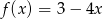 dla każdej liczby z przedziału
dla każdej liczby z przedziału 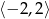 . Zbiorem wartości tej funkcji jest przedział
. Zbiorem wartości tej funkcji jest przedział
A) 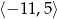 B)
B) 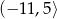 C)
C) 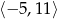 D)
D) 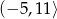
O funkcji liniowej 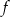 wiadomo, że
wiadomo, że 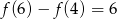 i
i 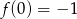 . Zatem
. Zatem
A) 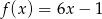 B)
B) 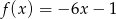 C)
C) 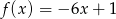 D)
D) 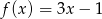
O funkcji liniowej 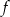 wiadomo, że
wiadomo, że 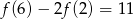 i
i 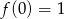 . Zatem
. Zatem
A) 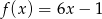 B)
B) 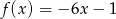 C)
C) 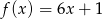 D)
D) 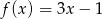
O funkcji liniowej 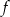 wiadomo, że
wiadomo, że 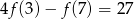 i
i 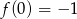 . Zatem
. Zatem
A) 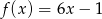 B)
B) 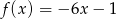 C)
C) 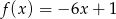 D)
D) 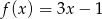
Funkcja liniowa 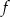 jest opisana wzorem
jest opisana wzorem 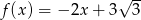 . Zatem liczba
. Zatem liczba 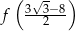 jest
jest
A) złożona B) pierwsza C) ujemna D) niewymierna
Funkcja liniowa 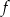 jest opisana wzorem
jest opisana wzorem 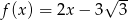 . Zatem liczba
. Zatem liczba 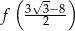 jest
jest
A) dodatnia B) pierwsza C) ujemna D) niewymierna
Funkcja liniowa 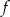 jest opisana wzorem
jest opisana wzorem 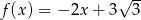 . Zatem liczba
. Zatem liczba 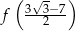 jest
jest
A) złożona B) pierwsza C) ujemna D) niewymierna
