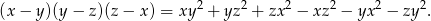Wykaż, że istnieje liczba dodatnia  , dla której
, dla której 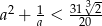 .
.
/Szkoła średnia/Nierówności/Udowodnij...
Udowodnij, że jeżeli 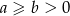 to
to 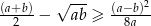 .
.
Wykaż, że dla dowolnych dodatnich liczb 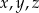 spełniona jest nierówność
spełniona jest nierówność
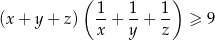
Uzasadnij, że jeżeli 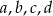 są liczbami dodatnimi to
są liczbami dodatnimi to
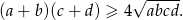
Udowodnij, że dla każdej liczby rzeczywistej  i każdej liczby rzeczywistej
i każdej liczby rzeczywistej 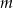 prawdziwa jest nierówność
prawdziwa jest nierówność 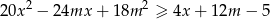 .
.
Wykaż, że dla każdej liczby rzeczywistej  i dla każdej liczby rzeczywistej
i dla każdej liczby rzeczywistej 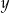 prawdziwa jest nierówność
prawdziwa jest nierówność 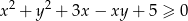 .
.
Udowodnij, że dla każdej liczby rzeczywistej  i każdej liczby rzeczywistej
i każdej liczby rzeczywistej 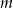 prawdziwa jest nierówność
prawdziwa jest nierówność 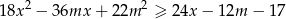 .
.
Udowodnij, że dla każdej liczby rzeczywistej  i każdej liczby rzeczywistej
i każdej liczby rzeczywistej 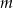 prawdziwa jest nierówność
prawdziwa jest nierówność 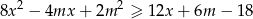 .
.
Wykaż, że dla dowolnych liczb rzeczywistych  i
i 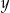 takich, że
takich, że 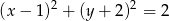 , prawdziwa jest nierówność
, prawdziwa jest nierówność 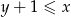 .
.
Wykaż, że dla dowolnej liczby rzeczywistej 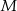 nierówność
nierówność
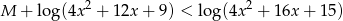
ma przynajmniej jedno rozwiązanie w przedziale 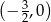 .
.
Wykaż, że dla dowolnych liczb rzeczywistych 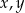 prawdziwa jest nierówność
prawdziwa jest nierówność
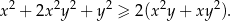
Wykaż, że dla dowolnych liczb rzeczywistych 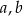 prawdziwa jest nierówność
prawdziwa jest nierówność
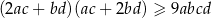
Udowodnij, że jeżeli 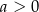 to dla wszystkich
to dla wszystkich 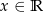 spełniona jest nierówność
spełniona jest nierówność 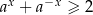 .
.
Wykaż, że dla wszystkich dodatnich liczb rzeczywistych 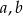 prawdziwa jest nierówność
prawdziwa jest nierówność 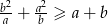 .
.
Wykaż, że dla dowolnych różnych liczb rzeczywistych 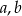 prawdziwa jest nierówność
prawdziwa jest nierówność
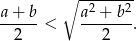
Wykaż, że jeśli 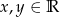 to
to 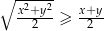 .
.
Uzasadnij, że jeżeli 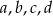 są liczbami dodatnimi to
są liczbami dodatnimi to
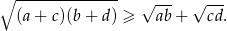
Wykaż, że dla 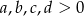 prawdziwa jest nierówność
prawdziwa jest nierówność 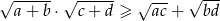 .
.
Wykaż, że dla każdej liczby rzeczywistej  oraz dla każdej liczby rzeczywistej
oraz dla każdej liczby rzeczywistej 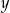 , spełniających warunek
, spełniających warunek 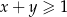 , prawdziwa jest nierówność
, prawdziwa jest nierówność
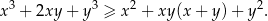
Wykaż, że dla każdej liczby rzeczywistej  oraz dla każdej liczby rzeczywistej
oraz dla każdej liczby rzeczywistej 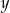 , spełniających warunek
, spełniających warunek 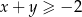 , prawdziwa jest nierówność
, prawdziwa jest nierówność
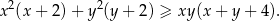
Wykaż, że dla każdej liczby rzeczywistej  i dla każdej liczby rzeczywistej
i dla każdej liczby rzeczywistej 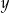 takich, że
takich, że 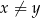 , spełniona jest nierówność
, spełniona jest nierówność
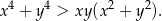
Udowodnij, że dla dowolnych liczb nieujemnych  i
i 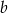 prawdziwa jest nierówność
prawdziwa jest nierówność
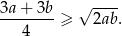
Wykaż, że dla dowolnej liczby dodatniej  prawdziwa jest nierówność
prawdziwa jest nierówność
Udowodnij, że dla każdych dwóch liczb rzeczywistych 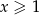 i
i 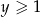 prawdziwa jest nierówność
prawdziwa jest nierówność
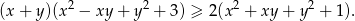
Udowodnij, że dla każdych dwóch liczb rzeczywistych 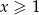 i
i 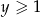 prawdziwa jest nierówność
prawdziwa jest nierówność
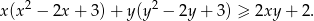
Wykaż, że dla każdej liczby rzeczywistej dodatniej  i dla każdej liczby rzeczywistej dodatniej
i dla każdej liczby rzeczywistej dodatniej 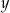 takiej, że
takiej, że 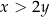 , prawdziwa jest nierówność
, prawdziwa jest nierówność
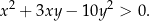
Wykaż, że dla wszystkich liczb rzeczywistych 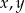 prawdziwa jest nierówność
prawdziwa jest nierówność 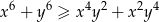 .
.
Udowodnij, że dla dowolnych liczb rzeczywistych 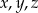 takich, że
takich, że 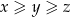 , prawdziwa jest nierówność
, prawdziwa jest nierówność
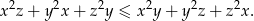
Możesz skorzystać z tożsamości