Wykaż, że dla każdych liczb rzeczywistych  oraz
oraz  prawdziwa jest nierówność
prawdziwa jest nierówność
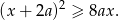
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Wykaż, że dla każdych liczb rzeczywistych  oraz
oraz  prawdziwa jest nierówność
prawdziwa jest nierówność
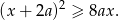
Wykaż, że dla każdej liczby rzeczywistej  i dla każdej liczby rzeczywistej
i dla każdej liczby rzeczywistej 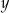 takich, że
takich, że 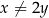 , prawdziwa jest nierówność
, prawdziwa jest nierówność
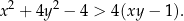
Wykaż, że dla każdej liczby rzeczywistej  i każdej liczby rzeczywistej
i każdej liczby rzeczywistej 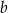 spełniona jest nierówność
spełniona jest nierówność
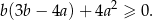
Wykaż, że dla każdej liczby rzeczywistej  i każdej liczby rzeczywistej
i każdej liczby rzeczywistej 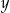 takich, że
takich, że 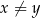 prawdziwa jest nierówność
prawdziwa jest nierówność
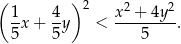
Wykaż, że dla dowolnych różnych liczb rzeczywistych  i
i 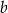 prawdziwa jest nierówność
prawdziwa jest nierówność
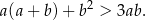
Wykaż, że dla każdej liczby rzeczywistej  i dla każdej liczby rzeczywistej
i dla każdej liczby rzeczywistej 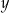 takich, że
takich, że 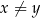 , prawdziwa jest nierówność
, prawdziwa jest nierówność
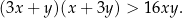
Wykaż, że dla dowolnych liczb rzeczywistych  i
i 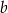 prawdziwa jest nierówność
prawdziwa jest nierówność
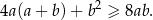
Wykaż, że dla każdej liczby rzeczywistej  i każdej liczby rzeczywistej
i każdej liczby rzeczywistej 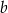 spełniona jest nierówność
spełniona jest nierówność
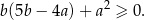
Wykaż, że dla dowolnej liczby całkowitej 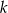 prawdziwa jest nierówność
prawdziwa jest nierówność 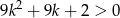 .
.
Wykaż, że dla dowolnej liczby całkowitej 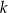 prawdziwa jest nierówność
prawdziwa jest nierówność 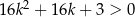 .
.
Udowodnij, że dla dowolnych różnych liczb rzeczywistych 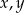 prawdziwa jest nierówność
prawdziwa jest nierówność
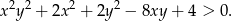
Udowodnij, że dla dowolnych różnych liczb rzeczywistych 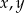 prawdziwa jest nierówność
prawdziwa jest nierówność
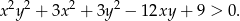
Udowodnij, że dla dowolnych różnych liczb rzeczywistych 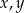 prawdziwa jest nierówność
prawdziwa jest nierówność
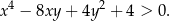
Wykaż, że dla dowolnych liczb rzeczywistych 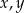 prawdziwa jest nierówność
prawdziwa jest nierówność
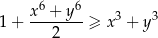
Wykaż, że dla wszystkich liczb rzeczywistych 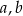 i
i  takich, że
takich, że 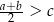 i
i 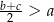 , prawdziwa jest nierówność
, prawdziwa jest nierówność
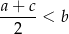
Wykaż, że dla wszystkich liczb rzeczywistych 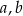 i
i  takich, że
takich, że 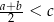 i
i 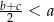 , prawdziwa jest nierówność
, prawdziwa jest nierówność
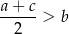
Wykaż, że dla każdej liczby rzeczywistej  i każdej liczby rzeczywistej
i każdej liczby rzeczywistej 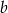 prawdziwa jest nierówność
prawdziwa jest nierówność
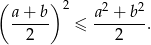
Wykaż, że dla każdej liczby rzeczywistej  i każdej liczby rzeczywistej
i każdej liczby rzeczywistej 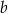 takich, że
takich, że 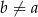 , spełniona jest nierówność
, spełniona jest nierówność
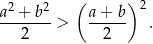
Wykaż, że dla każdych czterech liczb dodatnich 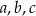 i
i 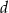 takich, że
takich, że 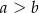 i
i 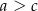 spełniona jest nierówność
spełniona jest nierówność
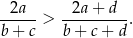
Wykaż, że jeżeli 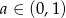 i
i 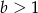 to prawdziwa jest nierówność
to prawdziwa jest nierówność
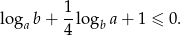
Wykaż, że jeżeli 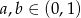 to prawdziwa jest nierówność
to prawdziwa jest nierówność
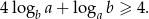
Uzasadnij, że dla dowolnych liczb dodatnich  i
i 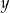 prawdziwa jest nierówność
prawdziwa jest nierówność
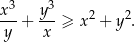
Uzasadnij, że dla dowolnych liczb dodatnich  i
i 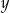 prawdziwa jest nierówność
prawdziwa jest nierówność
Wykaż, ze dla dowolnych liczb rzeczywistych 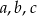 prawdziwa jest nierówność
prawdziwa jest nierówność
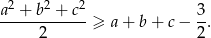
Niech 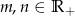 , udowodnij, że jeżeli
, udowodnij, że jeżeli 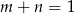 to prawdziwa jest nierówność
to prawdziwa jest nierówność 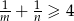 .
.
Wykaż, że dla wszystkich liczb rzeczywistych 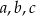 i
i 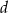 takich, że
takich, że 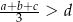 ,
, 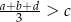 i
i 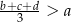 , prawdziwa jest nierówność
, prawdziwa jest nierówność
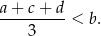
Udowodnij nierówność Bernoulliego: jeżeli 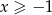 i
i 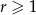 , to
, to 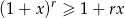 .
.
Udowodnij nierówność Bernoulliego: jeżeli 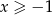 i
i 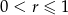 , to
, to 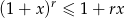 .
.
Wykaż, że dla 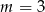 nierówność
nierówność 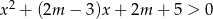 jest spełniona przez wszystkie liczby rzeczywiste
jest spełniona przez wszystkie liczby rzeczywiste  .
.
Dany jest wielomian 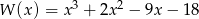 .
.
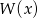 i
i 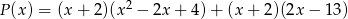 są równe.
są równe. 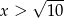 , to
, to 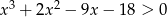 .
.Wykaż, że dla każdych trzech dodatnich liczb 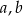 i
i  takich, że
takich, że 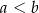 , spełniona jest nierówność
, spełniona jest nierówność
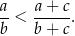
Wykaż, że dla każdych trzech liczb 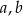 i
i  takich, że
takich, że 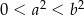 i
i 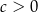 spełniona jest nierówność
spełniona jest nierówność
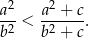
Wykaż, że rozwiązaniem nierówności 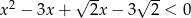 jest przedział
jest przedział 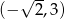 .
.
Uzasadnij, że jeśli liczby rzeczywiste 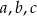 spełniają nierówności:
spełniają nierówności: 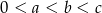 , to
, to
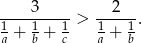
Wykaż, że dla każdej liczby rzeczywistej  prawdziwa jest nierówność:
prawdziwa jest nierówność:
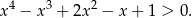
Udowodnij, że dla każdej liczby rzeczywistej  prawdziwa jest nierówność
prawdziwa jest nierówność
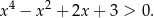
Udowodnij, że dla każdej liczby rzeczywistej  prawdziwa jest nierówność
prawdziwa jest nierówność
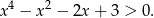
Udowodnij, że dla każdej liczby rzeczywistej  prawdziwa jest nierówność
prawdziwa jest nierówność
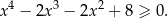
Wykaż, że dla każdej liczby rzeczywistej  prawdziwa jest nierówność:
prawdziwa jest nierówność:
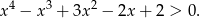
Udowodnij, że dla dowolnego kąta ostrego  prawdziwa jest nierówność
prawdziwa jest nierówność 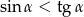 .
.
