Wykaż, że dla dowolnych liczb rzeczywistych 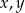 prawdziwa jest nierówność
prawdziwa jest nierówność
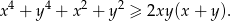
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Wykaż, że dla dowolnych liczb rzeczywistych 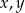 prawdziwa jest nierówność
prawdziwa jest nierówność
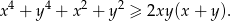
Uzasadnij, że liczba 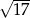 spełnia nierówność
spełnia nierówność 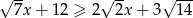 .
.
Udowodnij, że dla dowolnych liczb dodatnich  i
i 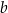 prawdziwa jest nierówność
prawdziwa jest nierówność
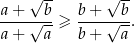
Udowodnij, że jeżeli 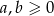 , to prawdziwa jest nierówność
, to prawdziwa jest nierówność 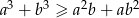 .
.
Wykaż, że dla wszystkich nieujemnych liczb rzeczywistych 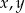 prawdziwa jest nierówność
prawdziwa jest nierówność 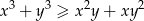 .
.
Funkcja 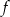 określona jest wzorem
określona jest wzorem 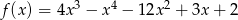 dla
dla 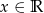 . Wykaż, że
. Wykaż, że
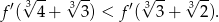
Wykaż, że dla dowolnych liczb rzeczywistych 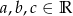 zachodzi nierówność
zachodzi nierówność
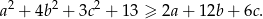
Wykaż, że jeżeli 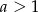 to prawdziwa jest nierówność
to prawdziwa jest nierówność
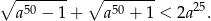
Wykaż, że dla każdej liczby dodatniej  i każdej liczby dodatniej
i każdej liczby dodatniej 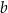 takich, że
takich, że 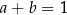 , prawdziwa jest nierówność
, prawdziwa jest nierówność
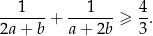
Wykaż, że dla dowolnych liczb rzeczywistych 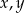 prawdziwa jest nierówność
prawdziwa jest nierówność
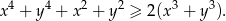
Wykaż, że dla dowolnych liczb rzeczywistych 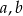 prawdziwa jest nierówność
prawdziwa jest nierówność
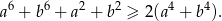
Udowodnij, że dla dowolnych liczb dodatnich 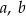 prawdziwa jest nierówność
prawdziwa jest nierówność
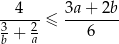
Udowodnij, że dla dowolnych liczb rzeczywistych 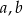 prawdziwa jest nierówność
prawdziwa jest nierówność
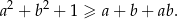
Wykaż, że dla każdej liczby 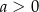 i dla każdej liczby
i dla każdej liczby 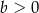 prawdziwa jest nierówność
prawdziwa jest nierówność
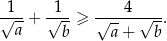
Udowodnij, że dla każdych dwóch liczb rzeczywistych dodatnich 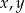 prawdziwa jest nierówność
prawdziwa jest nierówność 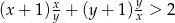 .
.
Wykaż, że dla dowolnej liczby rzeczywistej  spełniona jest nierówność
spełniona jest nierówność
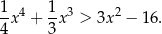
Wykaż, że dla dowolnych liczb rzeczywistych 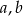 spełniona jest nierówność
spełniona jest nierówność
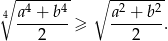
Wykaż, że jeżeli 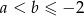 , to
, to 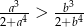 .
.
Uzasadnij, że funkcja 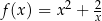 przyjmuje dla dodatnich argumentów wartości nie mniejsze niż 3.
przyjmuje dla dodatnich argumentów wartości nie mniejsze niż 3.
Wykaż, że dla każdej liczby rzeczywistej dodatniej  prawdziwa jest nierówność
prawdziwa jest nierówność
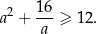
Wykaż, że dla każdej liczby rzeczywistej dodatniej  prawdziwa jest nierówność
prawdziwa jest nierówność
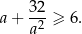
Uzasadnij, że dla każdej liczby dodatniej  prawdziwa jest nierówność
prawdziwa jest nierówność 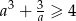 .
.
Dana jest funkcja 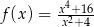 określona dla
określona dla 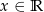 . Udowodnij, że dla każdej liczby rzeczywistej
. Udowodnij, że dla każdej liczby rzeczywistej  , spełniona jest nierówność
, spełniona jest nierówność 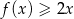 .
.
Wykaż, że jeżeli 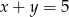 , to
, to 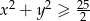 .
.
Wykaż, że jeżeli 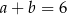 , to
, to 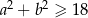 .
.
Wykaż, że jeżeli 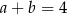 , to
, to 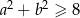 .
.
Wykaż, że dla każdej liczby 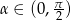 zachodzi nierówność
zachodzi nierówność 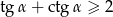 .
.
