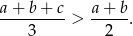Udowodnij, że jeżeli 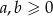 , to prawdziwa jest nierówność
, to prawdziwa jest nierówność 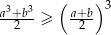 .
.
/Szkoła średnia/Nierówności/Udowodnij...
Wykaż, że dla każdej liczby rzeczywistej  większej od 2 i dla każdej liczby rzeczywistej
większej od 2 i dla każdej liczby rzeczywistej 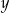 prawdziwa jest nierówność
prawdziwa jest nierówność 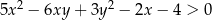 .
.
Wykaż, że dla każdej liczby rzeczywistej  i dla każdej liczby rzeczywistej
i dla każdej liczby rzeczywistej 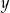 większej od 1 prawdziwa jest nierówność
większej od 1 prawdziwa jest nierówność 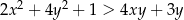 .
.
Wykaż, że dla każdej liczby rzeczywistej  mniejszej od
mniejszej od 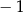 i dla każdej liczby rzeczywistej
i dla każdej liczby rzeczywistej 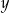 prawdziwa jest nierówność
prawdziwa jest nierówność 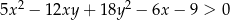 .
.
Udowodnij, że dla dowolnych liczb rzeczywistych 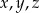 takich, że
takich, że 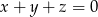 , prawdziwa jest nierówność
, prawdziwa jest nierówność 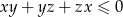 .
.
Możesz skorzystać z tożsamości 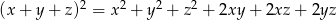 .
.
Wykaż, że dla dowolnych dodatnich liczb rzeczywistych  i
i 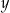 prawdziwa jest nierówność
prawdziwa jest nierówność
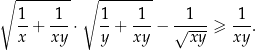
Wykaż, że dla dowolnych dodatnich liczb rzeczywistych 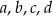 prawdziwa jest nierówność
prawdziwa jest nierówność
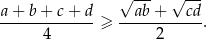
Udowodnij, że dla dowolnego kąta 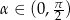 prawdziwa jest nierówność
prawdziwa jest nierówność
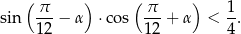
Udowodnij, że dla dowolnego kąta 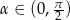 prawdziwa jest nierówność
prawdziwa jest nierówność
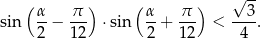
Wykaż, że jeżeli 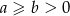 to
to
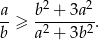
Wykaż, że prawdziwa jest nierówność 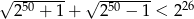 .
.
Udowodnij, że dla każdej liczby rzeczywistej  i dla każdej liczby rzeczywistej
i dla każdej liczby rzeczywistej 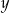 prawdziwa jest nierówność
prawdziwa jest nierówność
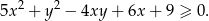
Wykaż, że dla dowolnych liczb rzeczywistych  i
i 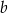 prawdziwa jest nierówność
prawdziwa jest nierówność
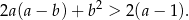
Wykaż, że dla każdej liczby rzeczywistej  i dla każdej liczby rzeczywistej
i dla każdej liczby rzeczywistej 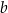 takiej, że
takiej, że 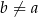 , prawdziwa jest nierówność
, prawdziwa jest nierówność
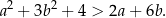
Wykaż, ze dla dowolnych liczb rzeczywistych 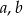 prawdziwa jest nierówność
prawdziwa jest nierówność 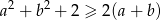 .
.
Wykaż, ze dla dowolnych liczb rzeczywistych 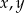 prawdziwa jest nierówność
prawdziwa jest nierówność 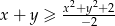 .
.
Wykaż, ze dla dowolnych liczb rzeczywistych 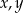 prawdziwa jest nierówność
prawdziwa jest nierówność 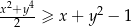 .
.
Wykaż, ze dla dowolnych liczb rzeczywistych 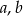 prawdziwa jest nierówność
prawdziwa jest nierówność 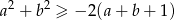 .
.
Wykaż, że dla każdej liczby rzeczywistej 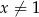 i dla każdej liczby rzeczywistej
i dla każdej liczby rzeczywistej 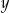 prawdziwa jest nierówność
prawdziwa jest nierówność
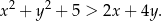
Wykaż, ze dla dowolnych liczb rzeczywistych 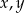 prawdziwa jest nierówność
prawdziwa jest nierówność 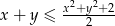 .
.
Wykaż, ze dla dowolnych liczb rzeczywistych 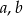 prawdziwa jest nierówność
prawdziwa jest nierówność 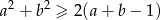 .
.
Wykaż, że dla dowolnych liczb rzeczywistych  i
i 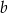 prawdziwa jest nierówność
prawdziwa jest nierówność
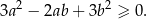
Wykaż, ze dla dowolnych liczb rzeczywistych 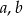 prawdziwa jest nierówność
prawdziwa jest nierówność 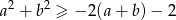 .
.
Wykaż, że dla dowolnych liczb rzeczywistych  i
i 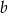 prawdziwa jest nierówność
prawdziwa jest nierówność
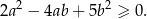
Wykaż, że dla każdej liczby rzeczywistej 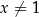 i dla każdej liczby rzeczywistej
i dla każdej liczby rzeczywistej 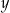 prawdziwa jest nierówność
prawdziwa jest nierówność
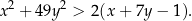
Wykaż, że dla każdej liczby rzeczywistej  i dla każdej liczby rzeczywistej
i dla każdej liczby rzeczywistej 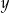 takich, że
takich, że 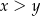 , spełniona jest nierówność
, spełniona jest nierówność
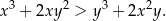
Wykaż, że jeżeli 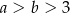 , to
, to 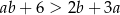 .
.
Korzystając z tego, że 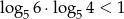 wykaż, że
wykaż, że
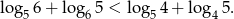
Wykaż, że jeżeli  jest kątem ostrym spełniającym warunek
jest kątem ostrym spełniającym warunek 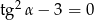 to
to 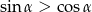 .
.
Wykaż, że dla dowolnych dodatnich liczb rzeczywistych  i
i 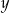 takich, że
takich, że 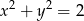 , prawdziwa jest nierówność
, prawdziwa jest nierówność 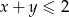 .
.
Wykaż, że dla każdej liczby rzeczywistej  i dla każdej liczby rzeczywistej
i dla każdej liczby rzeczywistej 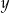 prawdziwa jest nierówność
prawdziwa jest nierówność 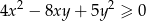 .
.
Udowodnij, że dla dowolnych liczb rzeczywistych 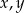 prawdziwa jest nierówność
prawdziwa jest nierówność 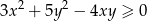 .
.
Wykaż, że dla każdej liczby rzeczywistej  i dla każdej liczby rzeczywistej
i dla każdej liczby rzeczywistej 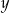 prawdziwa jest nierówność
prawdziwa jest nierówność 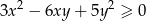 .
.
Wykaż, że dla każdej liczby rzeczywistej  i dla każdej liczby rzeczywistej
i dla każdej liczby rzeczywistej 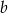 prawdziwa jest nierówność
prawdziwa jest nierówność 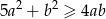 .
.
Wykaż, że dla każdej liczby rzeczywistej  i dla każdej liczby rzeczywistej
i dla każdej liczby rzeczywistej 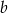 prawdziwa jest nierówność
prawdziwa jest nierówność 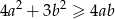 .
.
Udowodnij, że dla dowolnych dodatnich liczb rzeczywistych  i
i 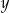 , takich że
, takich że 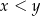 , i dowolnej dodatniej liczby rzeczywistej
, i dowolnej dodatniej liczby rzeczywistej  , prawdziwa jest nierówność
, prawdziwa jest nierówność 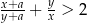 .
.
Udowodnij, że dla dowolnych dodatnich liczb rzeczywistych  i
i 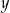 , takich że
, takich że 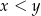 , i dowolnej dodatniej liczby rzeczywistej
, i dowolnej dodatniej liczby rzeczywistej 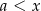 , prawdziwa jest nierówność
, prawdziwa jest nierówność 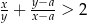 .
.
Wykaż, że dla dowolnych liczb ujemnych 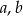 spełniona jest nierówność
spełniona jest nierówność
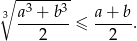
Wykaż, że
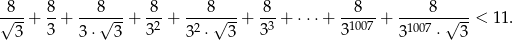
Uzasadnij, że jeśli liczby rzeczywiste 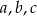 spełniają nierówności
spełniają nierówności 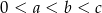 , to
, to