Wykaż, że jeżeli 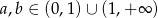 , to
, to
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Wykaż, że jeżeli 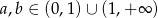 , to
, to
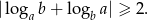
Wykaż, że jeżeli 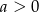 i
i 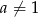 ,
, 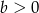 i
i 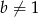 , to
, to 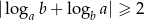 .
.
Wykaż, że dla dowolnych dodatnich liczb rzeczywistych 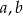 prawdziwa jest nierówność
prawdziwa jest nierówność
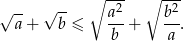
Wykaż, że dla dowolnej liczby 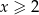 prawdziwa jest nierówność
prawdziwa jest nierówność 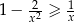 .
.
Wykaż, że jeżeli 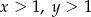 i
i 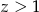 , to
, to 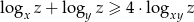 .
.
Wykaż, że jeżeli 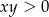 to
to 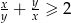 .
.
Udowodnij, że jeżeli 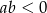 to
to 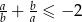 .
.
Wykaż, że jeśli 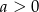 , to
, to 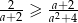 .
.
Wykaż, że jeżeli 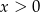 i
i 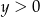 to
to 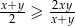 .
.
Udowodnij, że dla dowolnych liczb ujemnych 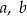 prawdziwa jest nierówność
prawdziwa jest nierówność
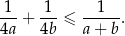
Wykaż, że jeżeli  i
i 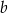 są liczbami rzeczywistymi dodatnimi, to
są liczbami rzeczywistymi dodatnimi, to 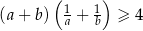 .
.
Wykaż, że dla każdej liczby 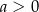 i dla każdej liczby
i dla każdej liczby 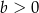 prawdziwa jest nierówność
prawdziwa jest nierówność
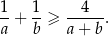
Wykaż, że jeśli 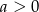 , to
, to 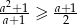 .
.
Udowodnij, że dla dowolnych liczb dodatnich 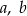 prawdziwa jest nierówność
prawdziwa jest nierówność
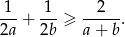
Wykaż, że dla dowolnych dodatnich liczb rzeczywistych 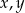 prawdziwa jest nierówność
prawdziwa jest nierówność 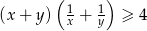 .
.
Wykaż, że dla każdej liczby rzeczywistej  prawdziwa jest nierówność
prawdziwa jest nierówność 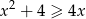 .
.
Wykaż, że dla każdej liczby rzeczywistej  prawdziwa jest nierówność
prawdziwa jest nierówność 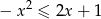 .
.
Wykaż, że dla każdej liczby rzeczywistej  prawdziwa jest nierówność
prawdziwa jest nierówność 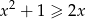 .
.
Uzasadnij, że jeśli liczby rzeczywiste 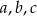 spełniają nierówności
spełniają nierówności 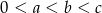 , to
, to
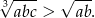
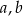 prawdziwa jest nierówność
prawdziwa jest nierówność 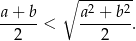
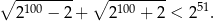
Wykaż, że dla dowolnych liczb rzeczywistych 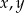 prawdziwa jest nierówność
prawdziwa jest nierówność
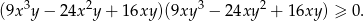
Uzasadnij, że jeżeli liczby rzeczywiste 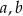 spełniają warunek
spełniają warunek 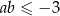 , to
, to 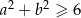 .
.
Funkcja 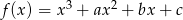 ma trzy różne miejsca zerowe:
ma trzy różne miejsca zerowe: 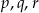 . Wykaż, że
. Wykaż, że
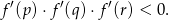
Wykaż, że jeżeli 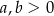 to
to 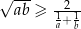 .
.
Wykaż, że jeżeli 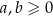 to
to 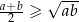 .
.
Liczby rzeczywiste  oraz
oraz 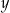 spełniają jednocześnie równanie
spełniają jednocześnie równanie 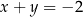 i nierówność
i nierówność
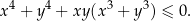
Wykaż, że 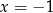 oraz
oraz 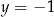 .
.
Liczby rzeczywiste  oraz
oraz 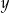 spełniają jednocześnie równanie
spełniają jednocześnie równanie 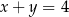 i nierówność
i nierówność
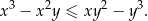
Wykaż, że 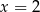 oraz
oraz 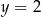 .
.
Liczby rzeczywiste  oraz
oraz 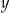 spełniają jednocześnie równanie
spełniają jednocześnie równanie 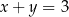 i nierówność
i nierówność
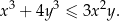
Wykaż, że 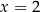 oraz
oraz 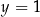 .
.
Dana jest nierówność kwadratowa z parametrem 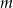 :
:
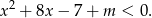
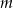 , dla których przedział
, dla których przedział 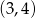 zawiera się w zbiorze rozwiązań tej nierówności.
zawiera się w zbiorze rozwiązań tej nierówności. 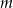 nierówność ta ma rozwiązanie w przedziale
nierówność ta ma rozwiązanie w przedziale 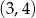 , to ma ona w tym przedziale nieskończenie wiele rozwiązań.
, to ma ona w tym przedziale nieskończenie wiele rozwiązań.Uzasadnij, że nierówność 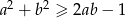 jest prawdziwa dla dowolnych liczb rzeczywistych
jest prawdziwa dla dowolnych liczb rzeczywistych  i
i 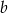 .
.
Wykaż, że dla każdych dwóch liczb rzeczywistych  i
i 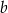 prawdziwa jest nierówność
prawdziwa jest nierówność
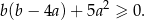
Wykaż, że dla każdych dwóch różnych liczb rzeczywistych  i
i 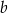 prawdziwa jest nierówność
prawdziwa jest nierówność
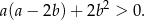
Wykaż, że dla każdej liczby rzeczywistej  różnej od 0 i każdej liczby rzeczywistej
różnej od 0 i każdej liczby rzeczywistej 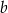 różnej od 0 spełniona jest nierówność
różnej od 0 spełniona jest nierówność
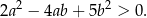
Wykaż, że jeżeli 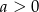 , to
, to 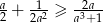 .
.
Wykaż, że jeżeli 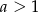 , to
, to 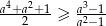 .
.
Udowodnij, że jeżeli 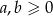 , to prawdziwa jest nierówność
, to prawdziwa jest nierówność 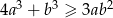 .
.
Uzasadnij, że jeżeli 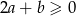 , to
, to 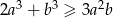 .
.
Wykaż, że dla dowolnych nieujemnych liczb rzeczywistych  ,
, 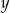 spełniona jest nierówność:
spełniona jest nierówność: 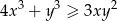 .
.
Udowodnij, że jeśli 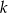 i
i  są liczbami naturalnymi oraz
są liczbami naturalnymi oraz 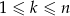 , to
, to 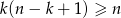 .
.
Wykaż, że jeżeli 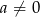 i
i 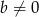 , to
, to 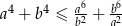 .
.
