Pole powierzchni całkowitej walca jest równe 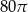 , a pole jego powierzchni bocznej jest 3 razy większe niż pole podstawy. Wysokość tego walca jest równa
, a pole jego powierzchni bocznej jest 3 razy większe niż pole podstawy. Wysokość tego walca jest równa
A) 3 B) 6 C) 9 D) 18
/Szkoła podstawowa/Zadania testowe
Na rysunku przedstawiono kwadraty 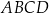 ,
, 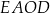 i
i 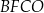 . Punkt
. Punkt 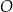 jest punktem przecięcia przekątnych kwadratu
jest punktem przecięcia przekątnych kwadratu 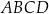 .
.

Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Pole kwadratu 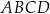 jest równe sumie pól kwadratów jest równe sumie pól kwadratów 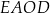 i i 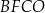 . . | P | F |
Obwód kwadratu 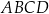 jest równy sumie długości wszystkich przekątnych kwadratów jest równy sumie długości wszystkich przekątnych kwadratów 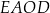 i i 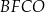 . . | P | F |
Cztery jednakowe drewniane elementy, każdy w kształcie prostopadłościanu o wymiarach 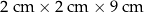 , przyklejono do metalowej płytki w sposób pokazany na rysunku I.
, przyklejono do metalowej płytki w sposób pokazany na rysunku I.

W ten sposób przygotowano formę, którą wypełniono masą gipsową, i tak otrzymano gipsowy odlew w kształcie prostopadłościanu, pokazany na rysunku II.
Objętość drewna, z którego zbudowano formę, jest równa A/B.
A) 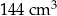 B)
B) 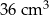
Objętość gipsowego odlewu jest równa C/D.
C) 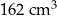 D)
D) 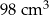
Cztery jednakowe drewniane elementy, każdy w kształcie prostopadłościanu o wymiarach 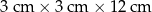 , przyklejono do metalowej płytki w sposób pokazany na rysunku I.
, przyklejono do metalowej płytki w sposób pokazany na rysunku I.
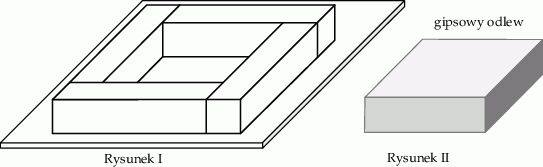
W ten sposób przygotowano formę, którą wypełniono masą gipsową, i tak otrzymano gipsowy odlew w kształcie prostopadłościanu, pokazany na rysunku II.
Objętość gipsowego odlewu jest równa C/D.
A) 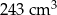 B)
B) 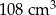
Objętość drewna, z którego zbudowano formę, jest równa A/B.
C) 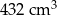 D)
D) 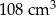
Jeżeli punkty 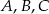 leżące na okręgu o środku
leżące na okręgu o środku  są wierzchołkami trójkąta równobocznego, to miara kąta środkowego
są wierzchołkami trójkąta równobocznego, to miara kąta środkowego 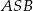 jest równa
jest równa
A) 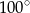 B)
B) 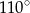 C)
C) 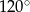 D)
D) 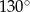
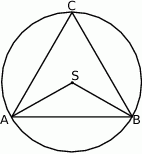
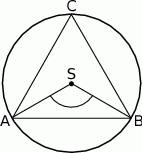
Punkty 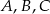 leżące na okręgu o środku
leżące na okręgu o środku  są wierzchołkami trójkąta równobocznego. Miara zaznaczonego na rysunku kąta środkowego
są wierzchołkami trójkąta równobocznego. Miara zaznaczonego na rysunku kąta środkowego  jest równa
jest równa
A) 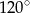 B)
B) 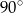 C)
C) 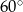 D)
D) 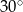
Pole podstawy stożka jest równe 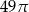 , a pole jego powierzchni bocznej jest 3 razy większe niż pole podstawy. Tworząca tego stożka ma długość
, a pole jego powierzchni bocznej jest 3 razy większe niż pole podstawy. Tworząca tego stożka ma długość
A) 7 B) 10,5 C) 21 D) 14
Turysta 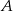 szedł ze schroniska w kierunku szczytu, natomiast turysta
szedł ze schroniska w kierunku szczytu, natomiast turysta  schodził ze szczytu w kierunku schroniska. Obaj szli tym samym szlakiem i tego samego dnia. Wykresy przedstawiają, na jakiej wysokości względem poziomu morza znajdowali się turyści w określonym czasie.
schodził ze szczytu w kierunku schroniska. Obaj szli tym samym szlakiem i tego samego dnia. Wykresy przedstawiają, na jakiej wysokości względem poziomu morza znajdowali się turyści w określonym czasie.
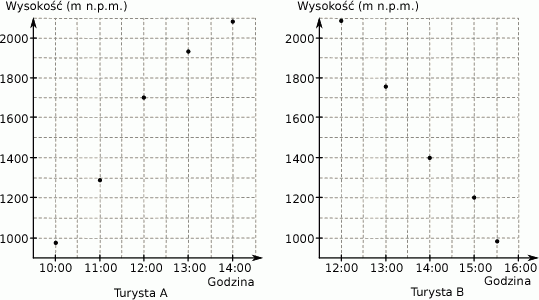
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Turyści spotkali się na szlaku między godziną 13:00 a 14:00. | P | F |
| Turyści spotkali się w miejscu położonym między 1700 a 2000 m n.p.m. | P | F |
Adam i Tomek tego samego dnia odbyli górską wycieczkę na Tarnicę. Obaj szli tym samym szlakiem, ale zanim Tomek zdobył szczyt, Adam zaczął już schodzić na dół. Wykresy przedstawiają na jakiej wysokości względem poziomu morza znajdowali się chłopcy – Tomek podczas wejścia na szczyt i Adam podczas zejścia na dół.
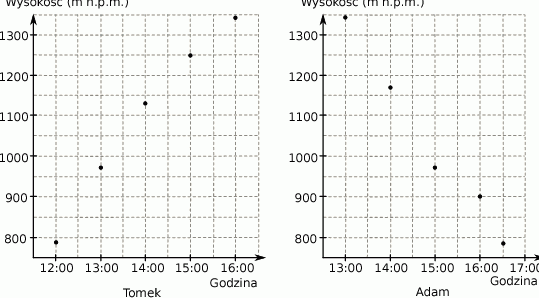
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Chłopcy spotkali się w miejscu położonym między 1000 a 1100 m n.p.m. | P | F |
| Chłopcy spotkali się na szlaku między godziną 14:00 a 15:00. | P | F |
Połowa uczestników wycieczki urodziła się w Polsce, co trzeci urodził się w Niemczech, a pięciu pozostałych we Francji. W wycieczce brało udział
A) 26 osób. B) 30 osób. C) 46 osób. D) 60 osób.
Co trzeci uczeń biorący udział w zawodach był uczniem klasy trzeciej, co czwarty był uczniem klasy piątej, a pozostałych 15 uczniów było uczniami klasy czwartej. W zawodach brało udział
A) 28 uczniów. B) 32 uczniów. C) 36 uczniów. D) 48 uczniów.
Emil kolekcjonuje modele samochodów. Co trzeci z jego modeli to model samochodu terenowego, co czwarty to model ciężarówki, a pozostałe 20 modeli to modele samochodów osobowych. Emil ma w swojej kolekcji
A) 64 modele. B) 48 modeli. C) 36 modeli. D) 32 modele.
Liczbę ogniw  łańcucha rowerowego można dobrać korzystając ze wzoru
łańcucha rowerowego można dobrać korzystając ze wzoru
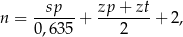
gdzie 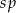 jest odległością w centymetrach od osi suportu do osi tylnej piasty,
jest odległością w centymetrach od osi suportu do osi tylnej piasty, 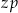 jest liczbą zębów największej zębatki z przodu, a
jest liczbą zębów największej zębatki z przodu, a 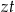 liczbą zębów największej zębatki z tyłu.
liczbą zębów największej zębatki z tyłu.
W tabeli podano niektóre parametry roweru.
| Liczba ogniw łańcucha | 114 |
| Liczba zębów największej zębatki z tyłu | 30 |
| Liczba zębów największej zębatki z przodu | 34 |
Jaka jest odległość osi suportu od osi tylnej piasty w tym rowerze?
A) 50,8 cm B) 48,26 cm C) 46,99 cm D) 45,72 cm
Liczbę ogniw  łańcucha rowerowego można dobrać korzystając ze wzoru
łańcucha rowerowego można dobrać korzystając ze wzoru
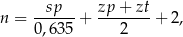
gdzie 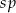 jest odległością w centymetrach od osi suportu do osi tylnej piasty,
jest odległością w centymetrach od osi suportu do osi tylnej piasty, 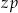 jest liczbą zębów największej zębatki z przodu, a
jest liczbą zębów największej zębatki z przodu, a 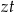 liczbą zębów największej zębatki z tyłu.
liczbą zębów największej zębatki z tyłu.
Jacek w swoim rowerze wymienił przednie zębatki tak, że zmniejszył liczbę zębów największej zębatki z 46 do 42 zębów. Jacek po wymianie zębatek powinien skrócić łańcuch o A/B.
A) 1 ogniwo B) 2 ogniwa
Karol w swoim rowerze wymienił zarówno przednie jak i tylne zębatki w ten sposób, że liczba zębów w każdej z zębatek zwiększyła się o 2. Karol po wymianie zębatek powinien wydłużyć łańcuch o C/D.
C) 1 ogniwo D) 2 ogniwa
Liczbę ogniw  łańcucha rowerowego można dobrać korzystając ze wzoru
łańcucha rowerowego można dobrać korzystając ze wzoru
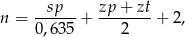
gdzie 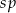 jest odległością w centymetrach od osi suportu do osi tylnej piasty,
jest odległością w centymetrach od osi suportu do osi tylnej piasty, 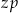 jest liczbą zębów największej zębatki z przodu, a
jest liczbą zębów największej zębatki z przodu, a 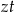 liczbą zębów największej zębatki z tyłu.
liczbą zębów największej zębatki z tyłu.
Jacek w swoim rowerze wymienił przednie zębatki tak, że zmniejszył liczbę zębów największej zębatki z 46 do 42 zębów.
Jacek po wymianie zębatek powinien skrócić łańcuch o
A) 1 ogniwo B) 2 ogniwa C) 3 ogniwa D) 4 ogniwa
Punkty 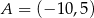 ,
, 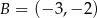 i
i 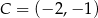 są kolejnymi wierzchołkami prostokąta
są kolejnymi wierzchołkami prostokąta 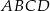 . Wierzchołek
. Wierzchołek 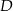 tego prostokąta ma współrzędne
tego prostokąta ma współrzędne
A) 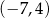 B)
B) 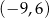 C)
C) 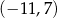 D)
D) 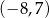
W układzie współrzędnych zaznaczono trzy kolejne wierzchołki prostokąta 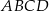 :
: 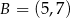 ,
, 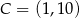 ,
, 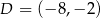 . Jakie współrzędne ma punkt A?
. Jakie współrzędne ma punkt A?
A) 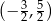 B)
B) 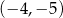 C)
C) 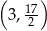 D)
D) 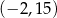
Wykonano następującą konstrukcję.
1. Narysowano trójkąt 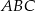 .
.
2. Wykreślono proste przechodzące przez wierzchołki trójkąta i równoległe do boków leżących naprzeciw tych wierzchołków.
3. Punkty przecięcia otrzymanych prostych oznaczono literami 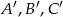 .
.
Wybierz P jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Pole trójkąta  jest dwa razy większe od pola trójkąta jest dwa razy większe od pola trójkąta 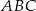 | P | F |
Obwód trójkąta 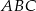 jest dwa ray mniejszy od obwodu trójkąta jest dwa ray mniejszy od obwodu trójkąta 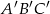 | P | F |
Dane są: kula o promieniu  , walec o promieniu podstawy
, walec o promieniu podstawy  i wysokości
i wysokości  , oraz stożek o promieniu podstawy
, oraz stożek o promieniu podstawy  i tworzącej długości
i tworzącej długości  .
.
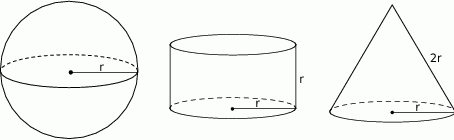
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Pole powierzchni całkowitej stożka jest równe polu powierzchni kuli. | P | F |
| Pole powierzchni całkowitej walca jest równe polu powierzchni kuli. | P | F |
Średnia arytmetyczna zestawu liczb 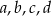 jest równa 20. Wtedy średnia arytmetyczna zestawu liczb
jest równa 20. Wtedy średnia arytmetyczna zestawu liczb 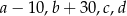 jest równa
jest równa
A) 10 B) 20 C) 25 D) 30
Średnia arytmetyczna trzech liczb: 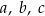 , jest równa 9. Średnia arytmetyczna sześciu liczb:
, jest równa 9. Średnia arytmetyczna sześciu liczb: 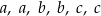 , jest równa
, jest równa
A) 9 B) 6 C) 4,5 D) 18
Średnia arytmetyczna liczb 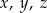 jest równa 4. Średnia arytmetyczna czterech liczb:
jest równa 4. Średnia arytmetyczna czterech liczb:
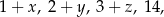
jest równa
A) 6 B) 9 C) 8 D) 13
Na osi liczbowej liczba 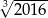 znajduje się między
znajduje się między
A) 40 i 50 B) 11 i 12 C) 12 i 13 D) 30 i 40
Na rysunku przedstawiono dwie figury. Figura I powstała przez usunięcie dwóch kwadratów jednostkowych z kwadratu o boku długości 6, a figura II powstała przez usunięcie dwóch kwadratów jednostkowych z prostokąta o bokach długości 4 i 8.
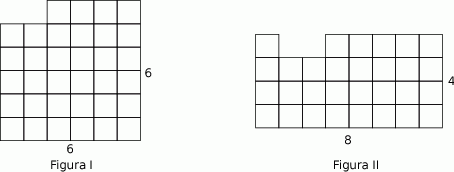
Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe.
| Obwód figury I jest równy obwodowi kwadratu o boku 6. | P | F |
| Obwód figury II jest większy od obwodu figury I. | P | F |
Na rysunku przedstawiono dwie figury. Figura I powstała przez usunięcie trzech kwadratów jednostkowych z kwadratu o boku długości 5, a figura II powstała przez usunięcie czterech kwadratów jednostkowych z prostokąta o bokach długości 3 i 7.
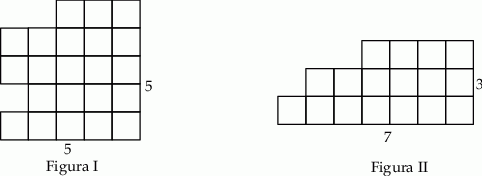
Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe.
| Obwód figury I jest równy obwodowi figury II. | P | F |
| Obwód figury II jest równy obwodowi kwadratu o boku 5. | P | F |
Różnica 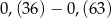 jest równa
jest równa
A) 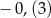 B)
B) 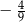 C)
C) 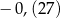 D)
D) 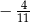
Liczbę  powiększono o 7, a następnie otrzymany wynik zwiększono 4–krotnie. Liczbę
powiększono o 7, a następnie otrzymany wynik zwiększono 4–krotnie. Liczbę 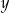 zwiększono 5–krotnie, a otrzymany wynik powiększono o 3. Która para wyrażeń algebraicznych poprawnie opisuje wykonane działania?
zwiększono 5–krotnie, a otrzymany wynik powiększono o 3. Która para wyrażeń algebraicznych poprawnie opisuje wykonane działania?
A) 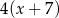 oraz
oraz 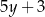 B)
B) 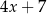 oraz
oraz 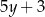
C) 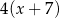 oraz
oraz 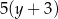 D)
D) 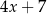 oraz
oraz 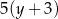
Liczbę  powiększono o 3, a następnie otrzymany wynik zwiększono 7–krotnie. Liczbę
powiększono o 3, a następnie otrzymany wynik zwiększono 7–krotnie. Liczbę 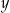 zwiększono 3–krotnie, a otrzymany wynik powiększono o 4. Która para wyrażeń algebraicznych poprawnie opisuje wykonane działania?
zwiększono 3–krotnie, a otrzymany wynik powiększono o 4. Która para wyrażeń algebraicznych poprawnie opisuje wykonane działania?
A) 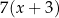 oraz
oraz 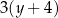 B)
B) 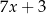 oraz
oraz 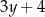
C) 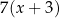 oraz
oraz 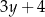 D)
D) 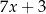 oraz
oraz 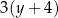
Grupie dwustu osób zadano pytanie: „Jaka jest twoja ulubiona dyscyplina sportu?”. Wyniki tej ankiety przedstawiono na wykresie.
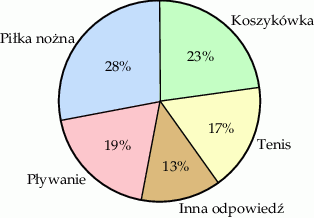
Z informacji podanych na diagramie wynika, że:
A) 28 osób jako ulubioną dyscyplinę podało piłkę nożną.
B) Łączna liczba odpowiedzi: „piłka nożna” i „tenis” jest równa liczbie wszystkich pozostałych odpowiedzi.
C) Liczba odpowiedzi „pływanie” była o 4 większa od liczby odpowiedzi „tenis”.
D) Liczba odpowiedzi „tenis” była o 6 mniejsza od liczby odpowiedzi „koszykówka”.
Miara kąta  zaznaczonego na rysunku jest równa
zaznaczonego na rysunku jest równa
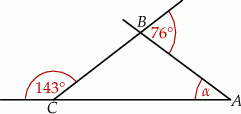
A) 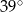 B)
B) 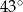 C)
C) 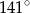 D)
D) 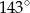
Średnia arytmetyczna wszystkich liczb pierwszych należących do przedziału 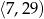 jest równa
jest równa
A) 15 B) 16,6 C) 17 D) 18,6
Średnia arytmetyczna wszystkich liczb pierwszych należących do przedziału 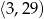 jest równa
jest równa
A) 14,1 B) 11,5 C) 12,25 D) 12,4
Średnia arytmetyczna wszystkich liczb pierwszych należących do przedziału 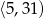 jest równa
jest równa
A) 17,2 B) 15,5 C) 16,3 D) 15,9
Dany jest przedział liczbowy 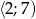 . Średnia arytmetyczna liczb pierwszych należących do tego przedziału jest równa
. Średnia arytmetyczna liczb pierwszych należących do tego przedziału jest równa
A) 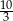 B)
B) 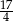 C) 4 D) 5
C) 4 D) 5
W pewnym banku oprocentowanie kredytu konsumpcyjnego przez cały marzec było równe 17%. Na początku kwietnia podwyższono oprocentowanie tego kredytu o 3 punkty procentowe, a na początku maja obniżono o 4 punkty procentowe. Oznacza to, że oprocentowanie tego kredytu konsumpcyjnego między kwietniem a majem zmalało o
A) 5% B) 3% C) 25% D) 20%

