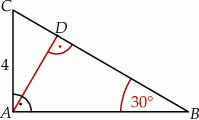
Odcinek 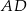 jest wysokością trójkąta prostokątnego
jest wysokością trójkąta prostokątnego 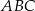 , w którym przyprostokątna
, w którym przyprostokątna 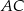 ma długość 4 cm i kąt ostry
ma długość 4 cm i kąt ostry 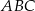 ma miarę
ma miarę 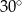 (zobacz rysunek).
(zobacz rysunek).
Kąt 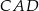 ma miarę A/B.
ma miarę A/B.
A) 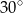 B)
B) 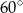
Odcinek 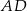 ma długość C/D.
ma długość C/D.
C) 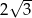 D)
D) 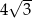
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Odcinek 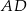 jest wysokością trójkąta prostokątnego
jest wysokością trójkąta prostokątnego 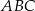 , w którym przyprostokątna
, w którym przyprostokątna 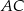 ma długość 4 cm i kąt ostry
ma długość 4 cm i kąt ostry 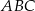 ma miarę
ma miarę 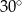 (zobacz rysunek).
(zobacz rysunek).

Kąt 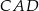 ma miarę A/B.
ma miarę A/B.
A) 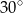 B)
B) 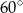
Odcinek 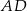 ma długość C/D.
ma długość C/D.
C) 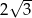 D)
D) 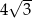
Odcinek 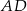 jest wysokością trójkąta prostokątnego
jest wysokością trójkąta prostokątnego 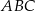 , w którym przeciwprostokątna
, w którym przeciwprostokątna 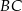 ma długość 4 cm i kąt ostry
ma długość 4 cm i kąt ostry 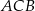 ma miarę
ma miarę 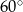 (zobacz rysunek).
(zobacz rysunek).
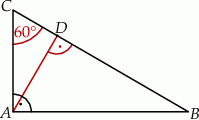
Kąt 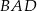 ma miarę A/B.
ma miarę A/B.
A) 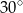 B)
B) 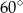
Odcinek 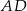 ma długość C/D.
ma długość C/D.
C) 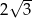 D)
D) 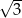
Z cyfr 2, 3 i 5 Ania utworzyła wszystkie możliwe liczby trzycyfrowe o różnych cyfrach. Które z poniższych zdań jest prawdziwe?
A) Wszystkie liczby utworzone przez Anię są nieparzyste.
B) Wszystkie liczby utworzone przez Anię są mniejsze od 530.
C) Dwie liczby utworzone przez Anię są podzielne przez 5.
D) Wśród liczb utworzonych przez Anię są liczby podzielne przez 3.
Z cyfr 3, 4 i 5 Kasia utworzyła wszystkie możliwe liczby trzycyfrowe o różnych cyfrach. Które z poniższych zdań jest prawdziwe?
A) Wszystkie liczby utworzone przez Kasię są nieparzyste.
B) Wszystkie liczby utworzone przez Kasię są podzielne przez 3.
C) Trzy liczby utworzone przez Kasię są podzielne przez 5.
D) Wśród liczb utworzonych przez Kasię są liczby podzielne przez 4.
Jeśli 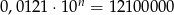 , to
, to  jest równe
jest równe
A) 12 B) 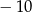 C) 9 D)
C) 9 D) 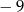
Jeśli 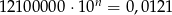 , to
, to  jest równe
jest równe
A) 12 B) 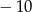 C) 9 D)
C) 9 D) 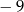
Jeśli 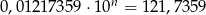 , to
, to  jest równe
jest równe
A) 4 B) -8 C) 5 D) -9
Jeśli 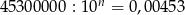 , to
, to  jest równe
jest równe
A) 9 B) 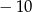 C) 10 D)
C) 10 D) 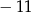
Liczba 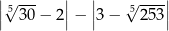 jest równa
jest równa
A) 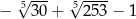 B)
B) 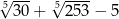
C) 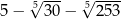 D)
D) 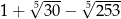
Dla zestawu liczb: 1, 3, 2, 4, 3
A) mediana jest równa 2 i średnia arytmetyczna jest równa 2,6.
B) mediana jest równa 3 i średnia arytmetyczna jest równa 3.
C) mediana jest równa 2 i średnia arytmetyczna jest równa 3.
D) mediana jest równa 3 i średnia arytmetyczna jest równa 2,6.
Wierzchołek 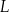 prostokąta przedstawionego na rysunku ma współrzędne
prostokąta przedstawionego na rysunku ma współrzędne

A) 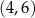 B)
B) 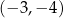 C)
C) 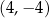 D)
D) 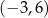
W układzie współrzędnych 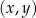 narysowano trapez
narysowano trapez 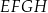 . Wszystkie współrzędne wierzchołków
. Wszystkie współrzędne wierzchołków 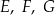 i
i 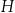 są liczbami całkowitymi.
są liczbami całkowitymi.
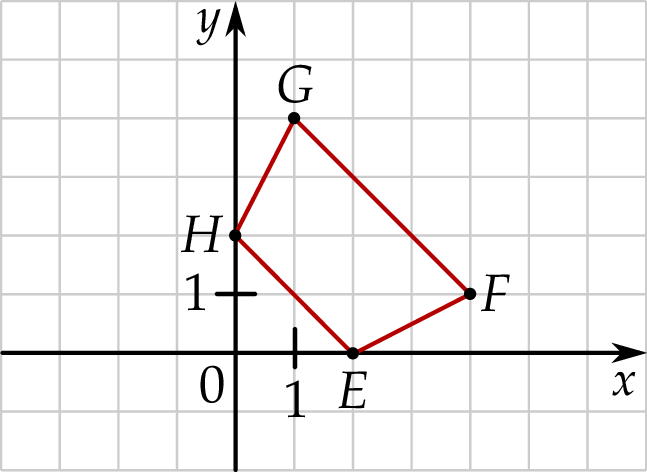
Punkty o współrzędnych 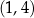 i
i 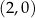 to wierzchołki
to wierzchołki
A) 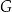 i
i 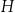 B)
B) 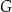 i
i 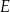 C)
C) 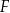 i
i 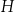 D)
D) 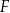 i
i 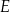
Wojtek narysował cztery figury (I–IV) składające się z kwadratów i trójkątów równobocznych (zobacz rysunek). Zamierza on dorysować do każdej figury jeden kwadrat albo jeden trójkąt, aby otrzymać z nich siatki graniastosłupa.
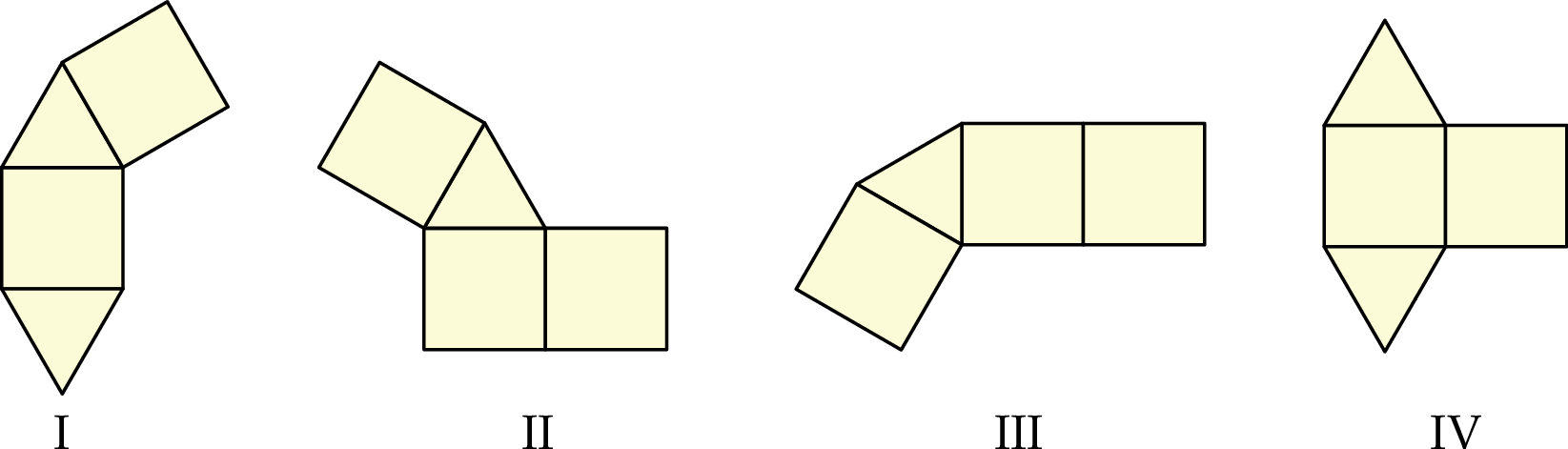
Z której figury nie da się w sposób zaplanowany przez Wojtka otrzymać siatki graniastosłupa?
A) I B) II C) III D) IV
Ile jest liczb dwucyfrowych parzystych, które przy dzieleniu przez 9 dają resztę 2 i jednocześnie są podzielne przez 7?
A) 1 B) 2 C) 3 D) 4
Dany jest trójkąt prostokątny 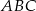 o przyprostokątnych długości 15 cm i 20 cm. Przeciwprostokątna trójkąta
o przyprostokątnych długości 15 cm i 20 cm. Przeciwprostokątna trójkąta 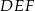 podobnego do trójkąta
podobnego do trójkąta 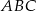 w skali 2:1 ma długość
w skali 2:1 ma długość
A) 25 cm B) 30 cm C) 40 cm D) 50 cm
Dany jest trójkąt prostokątny 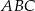 o przyprostokątnych długości 30 cm i 40 cm. Przeciwprostokątna trójkąta
o przyprostokątnych długości 30 cm i 40 cm. Przeciwprostokątna trójkąta 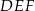 podobnego do trójkąta
podobnego do trójkąta 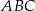 w skali 1:2 ma długość
w skali 1:2 ma długość
A) 15 cm B) 20 cm C) 25 cm D) 50 cm
Dany jest trójkąt równoramienny 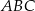 o podstawie długości 10 cm i polu
o podstawie długości 10 cm i polu 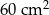 . Ramię trójkąta
. Ramię trójkąta 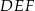 podobnego do trójkąta
podobnego do trójkąta 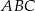 w skali 4:1 ma długość
w skali 4:1 ma długość
A) 52 cm B) 26 cm C) 13 cm D) 48 cm
Pomidory o masie 0,56 kg podczas suszenia straciły 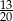 swojej masy. Po ususzeniu pomidory ważą:
swojej masy. Po ususzeniu pomidory ważą:
A) 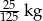 B)
B) 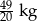 C)
C) 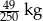 D)
D) 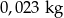
Jabłko o masie 0,16 kg podczas suszenia straciło 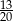 swojej masy. Po ususzeniu jabłko to waży:
swojej masy. Po ususzeniu jabłko to waży:
A) 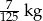 B)
B) 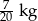 C)
C) 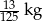 D)
D) 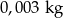
Brzoskwinia o masie 0,37 kg podczas suszenia straciła 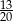 swojej masy. Po ususzeniu brzoskwinia ta waży:
swojej masy. Po ususzeniu brzoskwinia ta waży:
A) 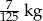 B)
B) 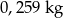 C)
C) 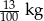 D)
D) 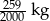
Liczba 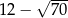 jest A/B.
jest A/B.
A) większa od 3 i mniejsza od 4. B) większa od 4 i mniejsza od 5.
Liczba 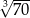 jest C/D.
jest C/D.
C) większa od 3 i mniejsza od 4. D) większa od 4 i mniejsza od 5.
Średnia arytmetyczna czterech liczb: 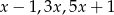 i
i 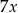 jest równa 72. Wynika stąd, że
jest równa 72. Wynika stąd, że
A) 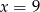 B)
B) 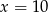 C)
C) 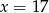 D)
D) 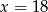
Średnia arytmetyczna czterech liczb dodatnich: 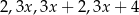 jest równa
jest równa 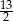 . Wynika stąd, że
. Wynika stąd, że
A) 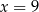 B)
B) 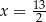 C)
C) 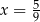 D)
D) 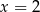
Średnia arytmetyczna czterech liczb: 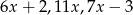 i
i 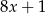 jest równa 88. Wynika stąd, że
jest równa 88. Wynika stąd, że
A) 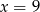 B)
B) 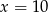 C)
C) 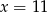 D)
D) 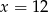
Średnia arytmetyczna pięciu liczb: 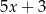 ,
, 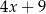 ,
, 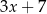 ,
, 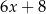 ,
, 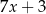 , jest równa 11. Wtedy
, jest równa 11. Wtedy  jest równe
jest równe
A) 1 B) 5 C) 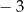 D)
D) 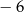
Średnia arytmetyczna czterech liczb dodatnich: 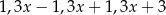 jest równa
jest równa 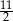 . Wynika stąd, że
. Wynika stąd, że
A) 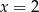 B)
B) 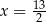 C)
C) 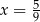 D)
D) 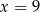
Średnia arytmetyczna pięciu liczb: 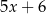 ,
, 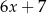 ,
, 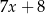 ,
, 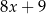 ,
, 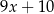 , jest równa 8. Wtedy
, jest równa 8. Wtedy  jest równe
jest równe
A) 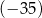 B) 0 C) 0,35 D) 35
B) 0 C) 0,35 D) 35
Wykres przedstawia zależność ilości paliwa pozostałego w baku samochodu (w litrach) od liczby przejechanych kilometrów.
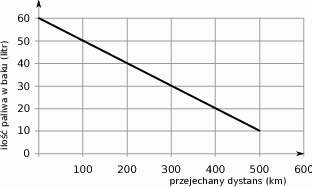
Ile paliwa pozostało w baku po przejechaniu 300 km?
A) 50 litrów B) 40 litrów C) 30 litrów D) 20 litrów
Wykres przedstawia zależność ilości paliwa pozostałego w baku samochodu (w litrach) od liczby przejechanych kilometrów.
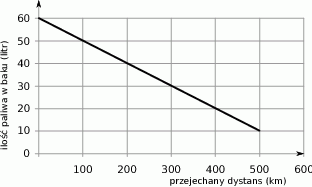
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Samochód spalił połowę początkowej ilości paliwa po przejechaniu 250 km. | P | F |
| Gdyby początkowo w baku było 40 litrów paliwa, to samochód mógłby przejechać 500 km. | P | F |
Wykres przedstawia zależność ilości paliwa pozostałego w baku samochodu (w litrach) od liczby przejechanych kilometrów.
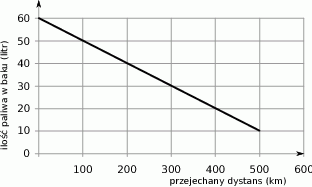
Ile paliwa potrzebuje ten samochód, aby przejechać 15 km?
A) 2 litry B) 1,5 litra C) 3 litry D) 2,5 litra
W tabeli zapisano trzy wyrażenia.
| I | 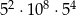 |
| II | 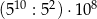 |
| III | 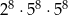 |
Które z tych wyrażeń są równe 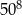 ?
?
A) Tylko I i II. B) Tylko II i III. C) Tylko II. D) Tylko III.
W tabeli zapisano trzy wyrażenia.
| I | 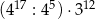 |
| II | 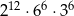 |
| III | 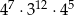 |
Które z tych wyrażeń są równe 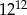 ?
?
A) Tylko I i III. B) Tylko II i III. C) Tylko I. D) Tylko III.
Samochód na pokonanie pierwszego odcinka trasy zużył 27 litrów benzyny. Na drugim odcinku trasy, mającym długość 150 km, zużył on dwa razy mniej benzyny niż na pierwszym odcinku. Średnie zużycie benzyny na kilometr było na każdym odcinku trasy takie samo. Średnie zużycie benzyny przez ten samochód na każde 100 km tej trasy było równe
A) 4,5 litra. B) 9 litrów. C) 13,5 litra. D) 18 litrów.
Samochód na pokonanie pierwszego odcinka trasy zużył 6,3 litra benzyny. Na drugim odcinku trasy, mającym długość 180 km, zużył on dwa razy więcej benzyny niż na pierwszym odcinku. Średnie zużycie benzyny na kilometr było na każdym odcinku trasy takie samo. Średnie zużycie benzyny przez ten samochód na każde 100 km tej trasy było równe
A) 7 litrów. B) 3,5 litra. C) 14 litrów. D) 4,2 litra.
Na wykresie przedstawiono, jak zmienia się masa porcji lodów z wafelkiem w zależności od liczby gałek lodów.
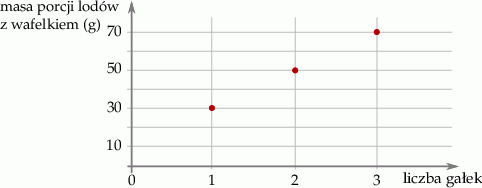
Jaką masę ma jedna gałka tych lodów bez wafelka?
A) 10 g B) 20 g C) 30 g D) 40 g
Na wykresie przedstawiono, jak zmienia się masa porcji lodów z wafelkiem w zależności od liczby gałek lodów.
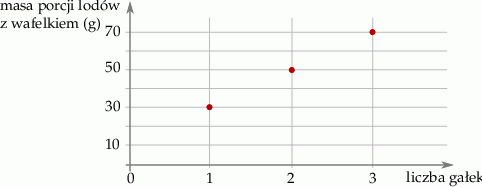
Jaką masę ma wafelek?
A) 10 g B) 20 g C) 30 g D) 40 g
Prostokąt o wymiarach 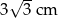 i
i 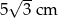 podzielono na 15 jednakowych kwadratów. Pole jednego kwadratu jest równe
podzielono na 15 jednakowych kwadratów. Pole jednego kwadratu jest równe
A) 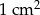 B)
B) 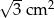 C)
C) 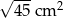 D)
D) 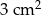
Prostokąt o wymiarach 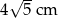 i
i 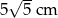 podzielono na 20 jednakowych kwadratów. Pole jednego kwadratu jest równe
podzielono na 20 jednakowych kwadratów. Pole jednego kwadratu jest równe
A) 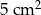 B)
B) 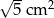 C)
C) 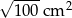 D)
D) 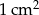
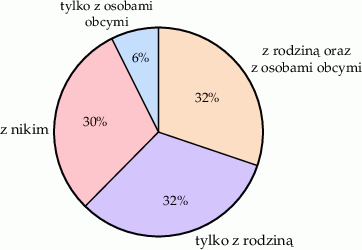
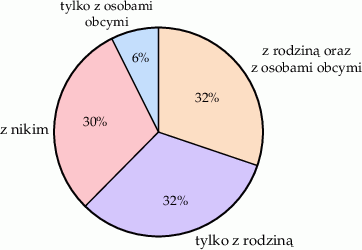
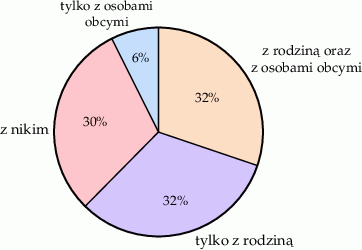
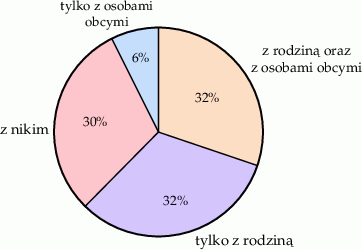
Podczas przeprowadzania ankiety na grupie 1100 osób zadano pytanie Z kim rozmawiałeś dziś przez telefon?. Wyniki ankiety przedstawiono na diagramie.
Podczas przeprowadzania ankiety na grupie 1100 osób zadano pytanie Z kim rozmawiałeś dziś przez telefon?. Wyniki ankiety przedstawiono na diagramie.
Podczas przeprowadzania ankiety na grupie 1100 osób zadano pytanie Z kim rozmawiałeś dziś przez telefon?. Wyniki ankiety przedstawiono na diagramie.
Podczas przeprowadzania ankiety na grupie 1100 osób zadano pytanie Z kim rozmawiałeś dziś przez telefon?. Wyniki ankiety przedstawiono na diagramie.
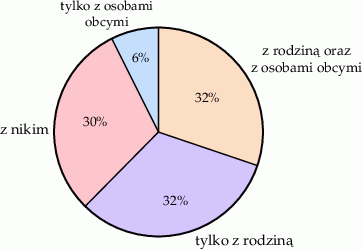
| Mniej niż połowa osób, które odbyły rozmowę telefoniczną rozmawiała tylko z rodziną. | P | F |
| Ponad 400 z ankietowanych osób rozmawiało tylko z rodziną. | P | F |
| Odsetek osób, które rozmawiały z rodziną był większy od odsetka osób, które nie rozmawiały z nikim o 2 punkty procentowe. | P | F |
| Odsetek osób, które rozmawiały tylko z obcymi jest mniejszy od odsetka osób, które rozmawiały tylko z rodziną o 26 punktów procentowych. | P | F |
Podczas przeprowadzania ankiety na grupie 1100 osób zadano pytanie Z kim rozmawiałeś dziś przez telefon?. Wyniki ankiety przedstawiono na diagramie.
Iloczyn 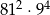 jest równy
jest równy
A) 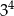 B)
B) 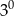 C)
C) 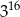 D)
D) 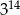
Liczba 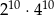 jest równa.
jest równa.
A) 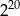 B)
B) 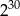 C)
C) 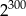 D)
D) 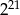
Liczba 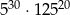 jest równa
jest równa
A) 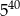 B)
B) 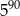 C)
C) 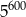 D)
D) 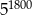
Iloczyn liczb 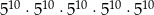 można przedstawić w postaci
można przedstawić w postaci
A) 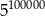 B)
B) 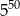 C)
C) 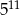 D)
D) 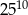
Liczba 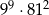 jest równa
jest równa
A) 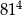 B)
B) 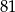 C)
C) 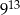 D)
D) 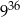
Liczba 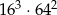 jest równa
jest równa
A) 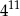 B)
B) 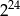 C)
C) 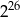 D)
D) 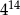
Czy iloczyn dowolnych pięciu kolejnych liczb całkowitych jest podzielny przez 10? Wybierz odpowiedź T (tak) albo N (nie) i jej uzasadnienie spośród oznaczonych literami A–C.
| Tak | Nie |
| ponieważ wśród dowolnych pięciu kolejnych liczb całkowitych | |
| A) | nie musi znajdować się liczba podzielna przez 10. |
| B) | jest co najmniej jedna liczba nieparzysta i co najmniej jedna liczba parzysta. |
| C) | jest co najmniej jedna liczba podzielna przez 5 i co najmniej jedna liczba parzysta. |
Czy suma dowolnych trzech kolejnych liczb całkowitych jest podzielna przez 3? Wybierz odpowiedź T (tak) albo N (nie) i jej uzasadnienie spośród oznaczonych literami A–C.
| Tak | Nie |
| ponieważ wśród dowolnych trzech kolejnych liczb całkowitych | |
| A) | musi znajdować się liczba podzielna przez 3. |
| B) | znajdują się liczby, które dają reszty: 0, 1 i 2 przy dzieleniu przez 3. |
| C) | znajduje się liczba, która nie jest podzielna przez 3. |
Czy iloczyn dowolnych czterech kolejnych liczb całkowitych dwucyfrowych jest podzielny przez 10? Wybierz odpowiedź T (tak) albo N (nie) i jej uzasadnienie spośród oznaczonych literami A–C.
| Tak | Nie |
| ponieważ wśród dowolnych czterech kolejnych liczb całkowitych | |
| A) | nie musi znajdować się liczba podzielna przez 5. |
| B) | jest co najmniej jedna liczba nieparzysta i co najmniej jedna liczba parzysta. |
| C) | jest co najmniej jedna liczba podzielna przez 5 i co najmniej jedna liczba parzysta. |
