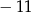W prostokątnym układzie współrzędnych umieszczono figurę przedstawioną na rysunku.
Przedstawiona figura
A) posiada jedną oś symetrii B) posiada dwie osie symetrii
C) posiada jeden środek symetrii D) posiada dwa środki symetrii
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
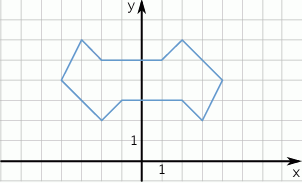
W prostokątnym układzie współrzędnych umieszczono figurę przedstawioną na rysunku.

Przedstawiona figura
A) posiada jedną oś symetrii B) posiada dwie osie symetrii
C) posiada jeden środek symetrii D) posiada dwa środki symetrii
W prostokątnym układzie współrzędnych umieszczono figurę przedstawioną na rysunku.
Przedstawiona figura
A) posiada jedną oś symetrii B) posiada dwie osie symetrii
C) posiada środek symetrii D) nie posiada osi symetrii
Liczbę 404 można zapisać w postaci 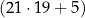 .
.
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Resztą z dzielenia liczby 404 przez 19 jest 5. | P | F |
| Jeśli liczbę 404 zmniejszymy o 5, to otrzymamy liczbę podzielną przez 21. | P | F |
Liczbę 400 można zapisać w postaci 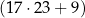 .
.
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Resztą z dzielenia liczby 400 przez 23 jest 17. | P | F |
| Jeśli liczbę 400 zwiększymy o 8, to otrzymamy liczbę podzielną przez 17. | P | F |
Czekolada o masie 20 dag przed promocją kosztowała 9,60 zł. Producent czekolady przygotował dwie promocje.

Czy dla klienta kupującego 120 dag czekolady bardziej opłacalna jest promocja II niż I? Wybierz odpowiedź T albo N i jej uzasadnienie spośród A, B albo C.
| Tak | Nie |
| ponieważ | |
| A) | w promocji I masa czekolady wzrośnie o 4 dag, natomiast w promocji II masa się nie zmieni. |
| B) | w promocji II 1 dag czekolady kosztuje mniej niż w promocji I. |
| C) | w promocji II trzeba kupić 6 czekolad, natomiast w promocji I – tylko 5. |
Pudełko margaryny o masie 40 dag przed promocją kosztowało 6,60 zł. Producent margaryny przygotował dwie promocje.

Czy dla klienta kupującego 440 dag margaryny bardziej opłacalna jest promocja II niż I? Wybierz odpowiedź T albo N i jej uzasadnienie spośród A, B albo C.
| Tak | Nie |
| ponieważ | |
| A) | w promocji I 1 dag margaryny kosztuje mniej niż w promocji II. |
| B) | w promocji II masa pudełka margaryny wzrośnie o 4 dag, natomiast w promocji I masa się nie zmieni. |
| C) | w promocji I trzeba kupić 11 pudełek margaryny, natomiast w promocji II – tylko 10. |
Suma długości wszystkich krawędzi ostrosłupa prawidłowego sześciokątnego jest równa 450. Krawędź boczna jest w tym ostrosłupie czterokrotnie dłuższa od krawędzi podstawy.
Długość krawędzi podstawy tego ostrosłupa jest równa
A) 15 B) 25 C) 50 D) 60
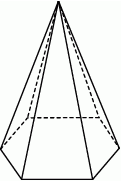
Suma długości wszystkich krawędzi ostrosłupa prawidłowego sześciokątnego jest równa 540. Krawędź boczna jest w tym ostrosłupie pięciokrotnie dłuższa od krawędzi podstawy.
Długość krawędzi podstawy tego ostrosłupa jest równa
A) 15 B) 25 C) 50 D) 60
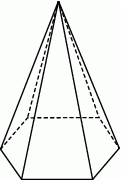
Wskaż wzór, który może opisywać funkcję, której wykres przedstawiono na poniższym rysunku.
A) 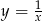 B)
B) 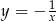 C)
C) 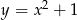 D)
D) 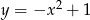
Wskaż wzór, który może opisywać funkcję, której wykres przedstawiono na poniższym rysunku.
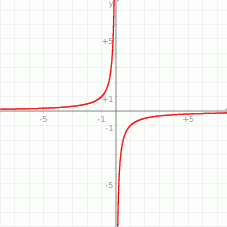
A) 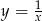 B)
B) 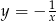 C)
C) 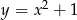 D)
D) 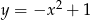
Wskaż wzór, który może opisywać funkcję, której wykres przedstawiono na poniższym rysunku.
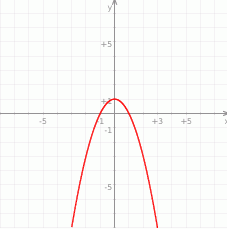
A) 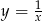 B)
B) 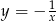 C)
C) 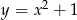 D)
D) 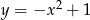
Liczba 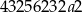 jest podzielna przez 4 jeżeli
jest podzielna przez 4 jeżeli
A) 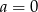 B)
B) 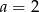 C)
C) 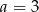 D)
D) 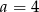
Liczba 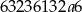 jest podzielna przez 4 jeżeli
jest podzielna przez 4 jeżeli
A) 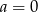 B)
B) 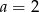 C)
C) 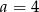 D)
D) 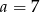
W liczbie pięciocyfrowej 258#4, podzielnej przez 4 i niepodzielnej przez 3, cyfrę dziesiątek zastąpiono znakiem „#”. Jakiej cyfry na pewno nie zastąpiono znakiem „#”?
A) 0 B) 4 C) 6 D) 8
Piotrek ma w swojej bibliotece tylko książki historyczne i biograficzne. Książek historycznych ma 9, co stanowi 30% wszystkich jego książek. Wynika stąd, że liczba książek biograficznych Piotrka, to
A) 21 B) 30 C) 16 D) 10
Karol ma w swojej bibliotece tylko książki przyrodnicze i sensacyjne. Książek przyrodniczych ma 12, co stanowi 40% wszystkich jego książek. Wynika stąd, że liczba książek sensacyjnych Karola, to
A) 21 B) 18 C) 36 D) 24
Gienek ma w swojej bibliotece tylko książki przygodowe i historyczne. Książek historycznych ma 21, co stanowi 35% wszystkich jego książek. Wynika stąd, że liczba książek przygodowych Gienka, to
A) 21 B) 31 C) 39 D) 43
Liczba osi symetrii figury przedstawionej na rysunku jest równa
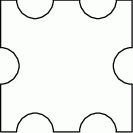
A) 1 B) 2 C) 3 D) 4
Liczba osi symetrii figury przedstawionej na rysunku jest równa

A) 4 B) 0 C) 2 D) 1
Dwie przecinające się proste utworzyły cztery kąty. Suma miar trzech z tych kątów jest równa 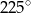 . Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Suma miar kątów ostrych wyznaczonych przez te proste jest równa 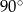 . . | P | F |
| Jeden z dwóch kątów przyległych jest trzy razy większy od drugiego kąta. | P | F |
Dwie przecinające się proste utworzyły cztery kąty. Suma miar trzech z tych kątów jest równa 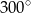 . Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Suma miar kątów ostrych wyznaczonych przez te proste jest równa 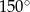 . . | P | F |
| Jeden z dwóch kątów przyległych jest dwa razy większy od drugiego kąta. | P | F |
Figurą, która ma oś symetrii, ale nie ma środka symetrii jest
A) równoległobok B) prostokąt C) trójkąt równoboczny D) romb
Pewna agencja reklamowa przygotowała zestawy promocyjne, które zawierały długopisy, ołówki i notesy. W każdym zestawie była taka sama liczba długopisów, ołówków i notesów, a łącznie we wszystkich zestawach znalazło się 225 długopisów, 300 ołówków i 150 notesów.
Ile maksymalnie przygotowano zestawów reklamowych?
A) 90 B) 75 C) 50 D) 25
Na spektakl dostępne były bilety normalne w jednakowej cenie oraz bilety ulgowe, z których każdy kosztował o 50% mniej niż normalny. Pani Anna za 3 bilety normalne i 2 bilety ulgowe zapłaciła 120 złotych. Na ten sam spektakl pan Jacek kupił 2 bilety normalne i 3 ulgowe, a pan Marek kupił 2 bilety normalne i 1 ulgowy. Pan Jacek zapłacił za bilety A/B.
A) 120 zł B) 105 zł
Pani Anna zapłaciła za bilety o C/D więcej niż pan Marek.
C) 45 zł D) 30 zł
Każdy bok trójkąta równobocznego  podzielono na 3 równe części i połączono kolejno punkty podziału, w wyniku czego otrzymano sześciokąt (rysunek).
podzielono na 3 równe części i połączono kolejno punkty podziału, w wyniku czego otrzymano sześciokąt (rysunek).
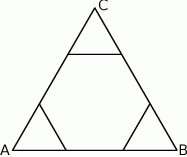
Które z poniższych zdań jest prawdziwe?
A) Sześciokąt jest foremny.
B) Pole sześciokąta jest równe polu trójkąta  .
.
C) Każdy kąt wewnętrzny sześciokąta ma miarę 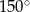 .
.
D) Obwód sześciokąta stanowi  obwodu trójkąta
obwodu trójkąta  .
.
W dodatniej liczbie trzycyfrowej cyfra dziesiątek jest średnią arytmetyczną jej pozostałych dwóch cyfr, a iloczyn cyfr setek i jedności jest równy 12. Ile jest liczb spełniających te warunki?
A) Jedna. B) Dwie. C) Trzy. D) Cztery.
Iloczyn 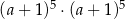 jest równy
jest równy
A) 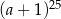 B)
B) 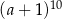 C)
C) 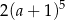 D)
D) 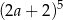
Rysunek przedstawia ostrosłup prosty.
Oceń, czy podane zdania są prawdziwe. Zaznacz P (prawda) lub F (fałsz).
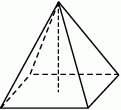
| Ściany boczne ostrosłupa są trójkątami prostokątnymi. | P | F |
| Liczba wszystkich krawędzi ostrosłupa jest parzysta. | P | F |
| Wszystkie ściany boczne ostrosłupa mają wspólny wierzchołek. | P | F |
Gdy od 17% liczby 21 odejmiemy 21% liczby 17, to otrzymamy
A) 0 B) 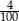 C) 3,57 D) 4
C) 3,57 D) 4
Gdy od 19% liczby 32 odejmiemy 16% liczby 19, to otrzymamy
A) 0 B) 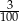 C) 3,04 D) 9,12
C) 3,04 D) 9,12
Gdy do 50% liczby 73 dodamy 73% liczby 50, to otrzymamy
A) 1 B) 73 C) 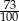 D) 100
D) 100
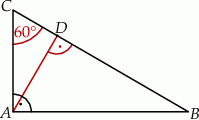
Odcinek 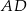 jest wysokością trójkąta prostokątnego
jest wysokością trójkąta prostokątnego 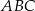 , w którym przyprostokątna
, w którym przyprostokątna 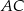 ma długość 4 cm i kąt ostry
ma długość 4 cm i kąt ostry 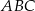 ma miarę
ma miarę 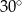 (zobacz rysunek).
(zobacz rysunek).
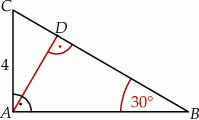
Kąt  ma miarę A/B.
ma miarę A/B.
A)  B)
B) 
Odcinek 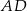 ma długość C/D.
ma długość C/D.
C) 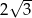 D)
D) 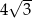
Odcinek 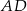 jest wysokością trójkąta prostokątnego
jest wysokością trójkąta prostokątnego 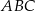 , w którym przeciwprostokątna
, w którym przeciwprostokątna 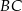 ma długość 4 cm i kąt ostry
ma długość 4 cm i kąt ostry 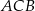 ma miarę
ma miarę 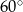 (zobacz rysunek).
(zobacz rysunek).
Kąt  ma miarę A/B.
ma miarę A/B.
A)  B)
B) 
Odcinek 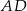 ma długość C/D.
ma długość C/D.
C) 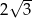 D)
D) 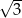
Z cyfr 2, 3 i 5 Ania utworzyła wszystkie możliwe liczby trzycyfrowe o różnych cyfrach. Które z poniższych zdań jest prawdziwe?
A) Wszystkie liczby utworzone przez Anię są nieparzyste.
B) Wszystkie liczby utworzone przez Anię są mniejsze od 530.
C) Dwie liczby utworzone przez Anię są podzielne przez 5.
D) Wśród liczb utworzonych przez Anię są liczby podzielne przez 3.
Z cyfr 3, 4 i 5 Kasia utworzyła wszystkie możliwe liczby trzycyfrowe o różnych cyfrach. Które z poniższych zdań jest prawdziwe?
A) Wszystkie liczby utworzone przez Kasię są nieparzyste.
B) Wszystkie liczby utworzone przez Kasię są podzielne przez 3.
C) Trzy liczby utworzone przez Kasię są podzielne przez 5.
D) Wśród liczb utworzonych przez Kasię są liczby podzielne przez 4.
Jeśli 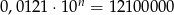 , to
, to  jest równe
jest równe
A) 12 B) 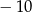 C) 9 D)
C) 9 D) 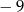
Jeśli 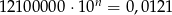 , to
, to  jest równe
jest równe
A) 12 B) 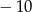 C) 9 D)
C) 9 D) 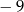
Jeśli 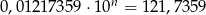 , to
, to  jest równe
jest równe
A) 4 B) -8 C) 5 D) -9
Jeśli 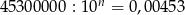 , to
, to  jest równe
jest równe
A) 9 B) 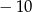 C) 10 D)
C) 10 D)