Na rysunku przedstawiono prostokąt, którego wymiary są opisane za pomocą wyrażeń.
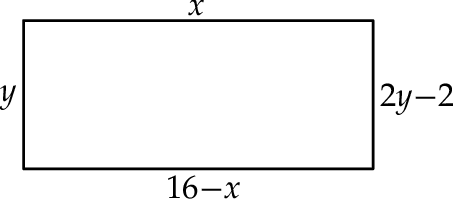
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Jeden z boków prostokąta ma długość 8. | P | F |
| Obwód prostokąta jest równy 20. | P | F |
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Na rysunku przedstawiono prostokąt, którego wymiary są opisane za pomocą wyrażeń.

Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Jeden z boków prostokąta ma długość 8. | P | F |
| Obwód prostokąta jest równy 20. | P | F |
Na rysunku przedstawiono prostokąt, którego wymiary są opisane za pomocą wyrażeń.
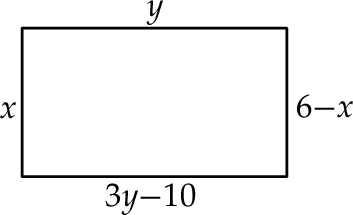
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Jeden z boków prostokąta ma długość 5. | P | F |
| Pole prostokąta jest równe 20. | P | F |
Przekątne rombu mają długości 24 i 10. Jaka jest długość boku rombu?
A) 13 B) 26 C) 6,5 D) 14
Liczbą większą od 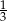 jest
jest
A) 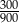 B)
B) 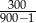 C)
C) 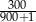 D)
D) 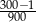
Liczbą mniejszą od 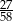 jest
jest
A)  B)
B)  C)
C)  D)
D) 
Liczbą mniejszą od 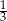 jest
jest
A) 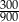 B)
B) 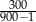 C)
C) 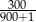 D)
D) 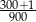
W tabeli przedstawiono informacje dotyczące półrocznej sprzedaży w pewnej firmie handlowej.
| Miesiąc | Wartość sprzedaży |
| 1 | 1500 zł |
| 2 | 800 zł |
| 3 | 2700 zł |
| 4 | 900 zł |
| 5 | 1200 zł |
| 6 | 900 zł |
W tabeli przedstawiono informacje dotyczące półrocznej sprzedaży w pewnej firmie handlowej.
| Miesiąc | Wartość sprzedaży |
| 1 | 1500 zł |
| 2 | 800 zł |
| 3 | 2700 zł |
| 4 | 900 zł |
| 5 | 1200 zł |
| 6 | 900 zł |
| Sprzedaż w 1 kwartale była wyższa niż sprzedaż w 2 kwartale. | P | F |
| Sprzedaż była najniższa w 4 miesiącu. | P | F |
W tabeli przedstawiono informacje dotyczące półrocznej sprzedaży w pewnej firmie handlowej.
| Miesiąc | Wartość sprzedaży |
| 1 | 1500 zł |
| 2 | 800 zł |
| 3 | 2700 zł |
| 4 | 900 zł |
| 5 | 1200 zł |
| 6 | 900 zł |
Na wycieczkę szkolną pojechali uczniowie dwóch klas: klasy IIa i IIb. Liczba uczniów klasy IIa stanowi  liczby uczniów klasy IIb. Ponadto
liczby uczniów klasy IIb. Ponadto  uczniów każdej z klas stanowią dziewczęta. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
uczniów każdej z klas stanowią dziewczęta. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Na wycieczkę pojechało dwa razy więcej dziewcząt niż chłopców. | P | F |
| Na wycieczkę pojechało 3 razy więcej uczniów klasy IIb niż klasy IIa. | P | F |
Pole trójkąta wynosi 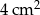 . Pole trójkąta do niego podobnego jest równe
. Pole trójkąta do niego podobnego jest równe 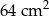 . Skala podobieństwa trójkąta większego do mniejszego jest równa
. Skala podobieństwa trójkąta większego do mniejszego jest równa
A) 2 B) 4 C) 6 D) 9
Pole trójkąta wynosi 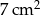 . Pole trójkąta do niego podobnego jest równe
. Pole trójkąta do niego podobnego jest równe 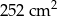 . Skala podobieństwa trójkąta mniejszego do większego jest równa
. Skala podobieństwa trójkąta mniejszego do większego jest równa
A) 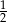 B)
B) 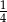 C)
C) 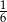 D)
D) 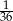
Działka ma powierzchnię 200 arów. Warzywa zajmują 130 arów, jabłonie rosną na 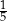 pozostałej części działki, a resztę działki zajmują śliwy. Śliwy zajmują powierzchnię
pozostałej części działki, a resztę działki zajmują śliwy. Śliwy zajmują powierzchnię
A) 14 arów. B) 30 arów. C) 56 arów. D) 70 arów.
Dane są liczby  i
i 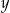 spełniające warunki:
spełniające warunki: 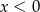 i
i 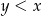 .
.
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Liczba 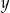 jest ujemna. jest ujemna. | P | F |
Liczba  jest większa od liczby jest większa od liczby 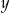 . . | P | F |
Dane są liczby  i
i 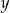 spełniające warunki:
spełniające warunki: 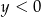 i
i 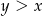 .
.
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Liczba  jest ujemna. jest ujemna. | P | F |
Liczba  jest większa od liczby jest większa od liczby 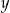 . . | P | F |
Jeden z kątów trójkąta prostokątnego 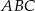 ma miarę
ma miarę 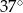 . Trójkąt
. Trójkąt 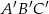 jest podobny do trójkąta
jest podobny do trójkąta 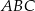 w skali 2:1. Miara najmniejszego kąta trójkąta
w skali 2:1. Miara najmniejszego kąta trójkąta 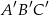 jest równa
jest równa
A) 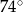 B)
B) 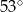 C)
C) 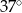 D)
D) 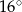
Jeden z kątów trójkąta prostokątnego 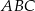 ma miarę
ma miarę 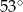 . Trójkąt
. Trójkąt 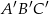 jest podobny do trójkąta
jest podobny do trójkąta 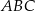 w skali 3:2. Miara najmniejszego kąta trójkąta
w skali 3:2. Miara najmniejszego kąta trójkąta 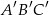 jest równa
jest równa
A) 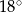 B)
B) 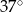 C)
C) 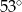 D)
D) 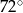
Wyrażenie 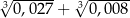 jest równe A/B.
jest równe A/B.
A) 0,5 B) 0,25
Wyrażenie 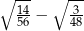 jest równe C/D.
jest równe C/D.
C) 0,25 D) 0,5
Liczba 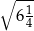 jest równa A/B.
jest równa A/B.
A) 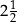 B)
B) 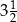
Liczba 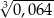 jest równa C/D.
jest równa C/D.
C) 0,4 D) 0,8
Liczbą wymierną nie jest liczba
A) 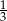 B)
B) 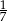 C)
C) 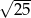 D)
D) 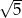
Liczbą wymierną nie jest liczba
A) 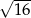 B)
B) 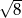 C)
C) 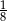 D)
D) 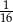
Liczbą wymierną nie jest liczba
A) 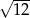 B)
B) 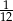 C)
C) 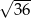 D)
D) 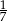
Dane są trzy liczby
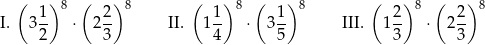
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Tylko jedna wśród liczb: I, II i III jest całkowita. | P | F |
| Liczba II jest większa od pozostałych dwóch liczb. | P | F |
Powierzchnia 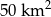 jest równa
jest równa
A) 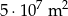 B)
B) 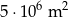 C)
C) 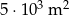 D)
D) 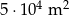
Liczby  i
i 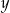 są dodatnie. Iloczyn potrojonej liczby
są dodatnie. Iloczyn potrojonej liczby  i liczby o 35% większej od liczby
i liczby o 35% większej od liczby 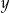 wyraża się wzorem
wyraża się wzorem
A) 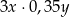 B)
B) 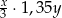 C)
C) 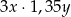 D)
D) 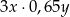
Liczby  i
i 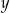 są dodatnie. Iloczyn trzeciej części liczby
są dodatnie. Iloczyn trzeciej części liczby  i liczby o 35% większej od liczby
i liczby o 35% większej od liczby 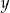 wyraża się wzorem
wyraża się wzorem
A) 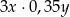 B)
B) 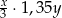 C)
C) 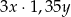 D)
D) 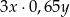
Liczby  i
i  są dodatnie. Iloczyn potrojonej liczby
są dodatnie. Iloczyn potrojonej liczby  i liczby o 35% mniejszej od liczby
i liczby o 35% mniejszej od liczby 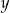 wyraża się wzorem
wyraża się wzorem
A) 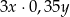 B)
B) 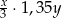 C)
C) 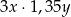 D)
D) 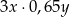
Na okręgu o środku w punkcie 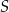 zaznaczono punkty
zaznaczono punkty 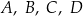 , a następnie narysowano odcinki
, a następnie narysowano odcinki 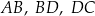 oraz
oraz 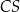 (zobacz rysunek).
(zobacz rysunek).

Trójkąt 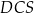 A/B równoramienny.
A/B równoramienny.
A) jest B) nie jest
Długość odcinka 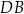 jest równa C/D.
jest równa C/D.
C) sumie długości odcinków 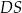 i
i 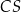 D) długości odcinka
D) długości odcinka 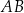
Jest dokładnie A/B liczb naturalnych 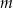 spełniających warunek
spełniających warunek 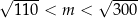 .
.
A) 7 B) 6
Są dokładnie C/D liczby naturalne 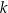 spełniające warunek
spełniające warunek 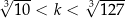 .
.
C) 4 D) 3
Prędkość średnia piechura na trasie 10 km wyniosła 5 km/h, a prędkość średnia rowerzysty na tej samej trasie była równa 20 km/h. O ile minut więcej zajęło pokonanie tej trasy piechurowi niż rowerzyście?
A) 30 minut B) 60 minut C) 90 minut D) 120 minut
Prędkość średnia samochodu osobowego na odcinku autostrady długości 50 km wyniosła 120 km/h, a prędkość średnia motocyklisty na tym samym odcinku autostrady wyniosła 100 km/h. O ile minut więcej zajęło pokonanie tego odcinka autostrady motocykliście niż kierowcy samochodu osobowego?
A) 4 minuty B) 5 minut C) 6 minut D) 8 minut
Prędkość średnia piechura na trasie 20 km wyniosła 5 km/h, a prędkość średnia rowerzysty na tej samej trasie była równa 10 km/h. O ile minut więcej zajęło pokonanie tej trasy piechurowi niż rowerzyście?
A) 180 minut B) 120 minut C) 90 minut D) 60 minut
Prędkość średnia piechura na trasie 9 km wyniosła 6 km/h, a prędkość średnia rowerzysty na tej samej trasie była równa 18 km/h. O ile minut więcej zajęło pokonanie tej trasy piechurowi niż rowerzyście?
A) 30 minut B) 60 minut C) 90 minut D) 120 minut
W pudełku było wyłącznie 6 kulek zielonych i 8 kulek niebieskich. Po dołożeniu do tego pudełka pewnej liczby kulek zielonych prawdopodobieństwo wylosowania kulki niebieskiej jest równe 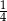 . Ile kulek zielonych dołożono do pudełka?
. Ile kulek zielonych dołożono do pudełka?
A) 10 B) 16 C) 18 D) 24
W pudełku było wyłącznie 9 kulek zielonych i 6 kulek niebieskich. Po dołożeniu do tego pudełka pewnej liczby kulek zielonych prawdopodobieństwo wylosowania kulki niebieskiej jest równe 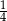 . Ile kulek zielonych dołożono do pudełka?
. Ile kulek zielonych dołożono do pudełka?
A) 10 B) 9 C) 18 D) 6
W turnieju szachowym wzięło udział 48 uczniów pewnego gimnazjum. Liczby uczestników turnieju z klas pierwszych, drugich i trzecich są do siebie w proporcji 3 : 8 : 5.
Jaki procent uczestników turnieju stanowili drugoklasiści?
A) 17% B) 24% C) 33% D) 50%
W turnieju szachowym wzięło udział 48 uczniów pewnego gimnazjum. Liczby uczestników turnieju z klas pierwszych, drugich i trzecich są do siebie w proporcji 3 : 8 : 5.
Liczba uczniów klas pierwszych, którzy wzięli udział w turnieju, jest równa
A) 8 B) 9 C) 10 D) 11
Liczby uczestników konkursu ortograficznego z klas pierwszych, drugich i trzecich gimnazjum są do siebie w proporcji 11 : 12 : 9.
Jaki procent uczestników konkursu stanowili drugoklasiści?
A) 60% B) 35% C) 37,5% D) 50%
Jeżeli 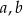 i
i  są długościami boków trójkąta oraz
są długościami boków trójkąta oraz  jest najdłuższym bokiem, to ten trójkąt jest:
jest najdłuższym bokiem, to ten trójkąt jest:
– prostokątny, gdy 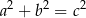
– rozwartokątny, gdy 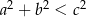
– ostrokątny, gdy 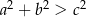 .
.
Z odcinków o długościach: 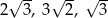
A) nie można zbudować trójkąta. B) można zbudować trójkąt prostokątny.
C) można zbudować trójkąt rozwartokątny. D) można zbudować trójkąt ostrokątny.
Jeżeli 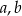 i
i  są długościami boków trójkąta oraz
są długościami boków trójkąta oraz  jest jego najdłuższym bokiem, to ten trójkąt jest:
jest jego najdłuższym bokiem, to ten trójkąt jest:
– prostokątny, gdy 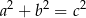
– rozwartokątny, gdy 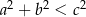
– ostrokątny, gdy 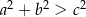 .
.
Z odcinków o długościach: 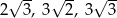
A) nie można zbudować trójkąta. B) można zbudować trójkąt prostokątny.
C) można zbudować trójkąt rozwartokątny. D) można zbudować trójkąt ostrokątny.
