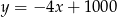Na rysunku przedstawiono pięciokąt foremny 
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Trójkąty 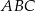 i i 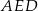 są przystające. są przystające. | P | F |
Jest 10 trójkątów o wierzchołkach w punktach 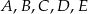 , które są przystające do trójkąta , które są przystające do trójkąta 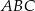 . . | P | F |
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Na rysunku przedstawiono pięciokąt foremny 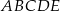

Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Trójkąty 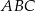 i i 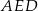 są przystające. są przystające. | P | F |
Jest 10 trójkątów o wierzchołkach w punktach 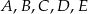 , które są przystające do trójkąta , które są przystające do trójkąta 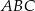 . . | P | F |
Dane są cztery wyrażenia:
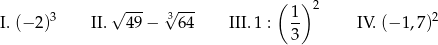
Największą wartość ma wyrażenie
A) I B) II C) III D) IV
Dane są trzy liczby:
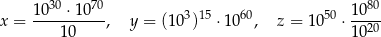
Która z tych liczb jest mniejsza od liczby 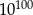 ?
?
A) Tylko  . B) Tylko
. B) Tylko 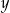 . C) Tylko
. C) Tylko  . D) Każda z liczb
. D) Każda z liczb 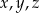 .
.
Dane są trzy liczby:
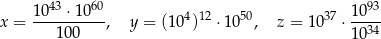
Która z tych liczb jest większa od liczby 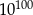 ?
?
A) Tylko  . B) Tylko
. B) Tylko  i
i 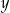 . C) Tylko
. C) Tylko  i
i  . D) Każda z liczb
. D) Każda z liczb  .
.
Ewa ma o 25% pieniędzy więcej niż Joasia. O ile procent Joasia ma mniej pieniędzy niż Ewa?
A) 25% B) 20% C) 50% D) 100%
Janek ma o 20% pieniędzy mniej niż Antek. O ile procent Antek ma więcej pieniędzy niż Janek?
A) 25% B) 20% C) 50% D) 100%
W układzie współrzędnych dane są punkty 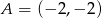 ,
, 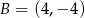 ,
, 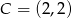 i
i 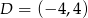 . Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Czworokąt 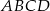 jest trapezem. jest trapezem. | P | F |
Czworokąt 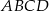 posiada oś symetrii. posiada oś symetrii. | P | F |
Szklane naczynie w kształcie prostopadłościanu o wymiarach 6 cm, 15 cm i 18 cm napełniono częściowo wodą i szczelnie zamknięto. Następnie naczynie postawiono na jego ścianie o największej powierzchni i wtedy woda sięgała do wysokości 4 cm. Kiedy naczynie postawiono na ścianie o najmniejszej powierzchni, to woda sięgała do wysokości
A) 8 cm B) 10 cm C) 12 cm D) 16 cm
Szklane naczynie w kształcie prostopadłościanu o wymiarach 9 cm, 12 cm i 21 cm napełniono częściowo wodą i szczelnie zamknięto. Następnie naczynie postawiono na jego ścianie o największej powierzchni i wtedy woda sięgała do wysokości 6 cm. Kiedy naczynie postawiono na ścianie o najmniejszej powierzchni, to woda sięgała do wysokości
A) 8 cm B) 10 cm C) 12 cm D) 14 cm
Wykonano następującą konstrukcję.
1. Narysowano trapez równoramienny  , w którym
, w którym 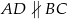 .
.
2. Wykreślono symetralne odcinków 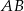 i
i 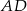 i ich punkt przecięcia oznaczono literą
i ich punkt przecięcia oznaczono literą 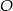 .
.
3. Narysowano okrąg o środku w punkcie 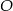 i promieniu
i promieniu 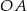 .
.
Skonstruowany w opisany powyżej sposób okrąg
A) przechodzi przez wszystkie wierzchołki tego trapezu.
B) jest styczny do wszystkich boków tego trapezu.
C) jest styczny do podstaw tego trapezu.
D) przechodzi przez środki ramion trapezu.
Małe trójkąty równoboczne o bokach długości 1 układano obok siebie tak, że uzyskiwano kolejne, coraz większe trójkąty równoboczne, według reguły przedstawionej na poniższym rysunku.
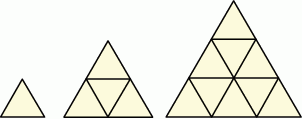
Ile małych trójkątów równobocznych należy użyć, aby ułożyć trójkąt równoboczny o podstawie równej 5?
A) 9 B) 16 C) 25 D) 50
Jeżeli 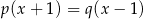 to
to
A) 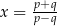 , gdy
, gdy 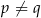 B)
B) 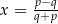 , gdy
, gdy 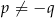
C) 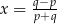 , gdy
, gdy 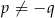 D)
D) 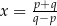 , gdy
, gdy 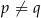
Jeżeli 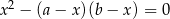 to
to
A) 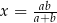 , gdy
, gdy 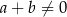 B)
B) 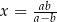 , gdy
, gdy 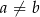
C) 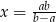 , gdy
, gdy 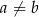 D)
D) 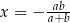 , gdy
, gdy 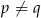
Dane są trzy wyrażenia:
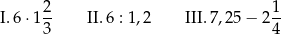
Liczbami całkowitymi są wartości wyrażeń
A) I, II i III B) Tylko I i II C) Tylko II i III D) Tylko I i III
Dane są trzy wyrażenia:
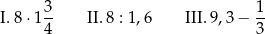
Liczbami całkowitymi są wartości wyrażeń
A) I, II i III B) Tylko I i II C) Tylko II i III D) Tylko I i III
Na rysunkach I–IV przedstawiono cztery pary trójkątów.
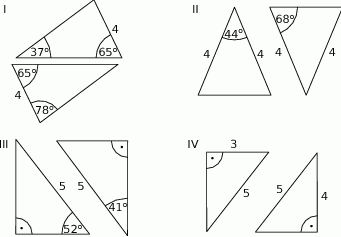
Na którym rysunku trójkąty nie są przystające?
A) I B) II C) III D) IV
Na rysunkach I–IV przedstawiono cztery pary trójkątów.
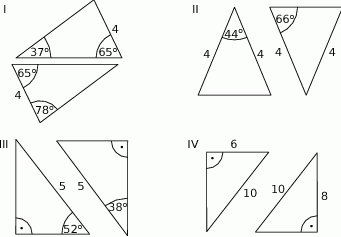
Na którym rysunku trójkąty nie są przystające?
A) I B) II C) III D) IV
Dane są cztery wyrażenia:
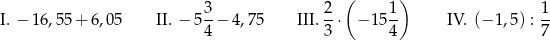
Wartość którego wyrażenia nie jest równa  ?
?
A) I B) II C) III D) IV
Dane są cztery wyrażenia:
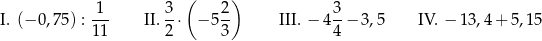
Wartość którego wyrażenia nie jest równa 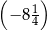 ?
?
A) I B) II C) III D) IV
Cena pewnego towaru w wyniku obniżki o 10% zmniejszyła się o 2 018 zł. Ten towar po tej obniżce kosztował
A) 20 180 zł B) 18 162 zł C) 2 108 zł D) 2 028 zł
Z 36 sześcianów o krawędziach długości 1 zbudowano graniastosłup prawidłowy czworokątny. Które wymiary, z podanych w tabeli, może mieć ten graniastosłup?
| I | 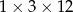 |
| II | 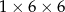 |
| III | 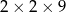 |
| IV | 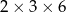 |
| V | 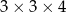 |
A) I, II i III B) III, IV i V C) I, II i IV D) II, III i V E) Wszystkie podane.
Z 9 sześcianów o krawędziach długości 2 zbudowano graniastosłup prawidłowy czworokątny. Które wymiary, z podanych w tabeli, może mieć ten graniastosłup?
| I | 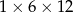 |
| II | 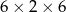 |
| III | 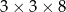 |
| IV | 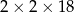 |
| V | 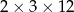 |
A) II, III i IV B) III i IV C) II i IV D) Wszystkie podane.
W poniższej tabeli zebrano zarobki wszystkich pracowników pewnej firmy handlowej.
| Imię pracownika | Zarobki |
| Kamila, Krzysztof, Stefan | 2800 zł |
| Zofia, Łukasz | 3000 zł |
| Ela, Marta | 3200 zł |
| Henryk | 3600 zł. |
Jaka jest średnia zarobków pracowników tej firmy?
A) 3050 zł B) 3150 zł C) 3200 zł D) 3250 zł
Liczbę  zaokrąglono do najbliższej liczby całkowitej i otrzymano
zaokrąglono do najbliższej liczby całkowitej i otrzymano 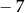 . O liczbie
. O liczbie 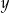 wiadomo, że jej odległość od
wiadomo, że jej odległość od  na osi liczbowej jest równa 7,35. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
na osi liczbowej jest równa 7,35. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Jeżeli 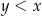 , to liczba , to liczba 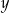 jest na pewno mniejsza niż jest na pewno mniejsza niż 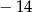 . . | P | F |
Jeżeli 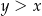 , to liczba , to liczba 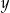 jest na pewno dodatnia. jest na pewno dodatnia. | P | F |
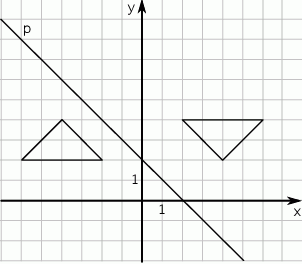
W prostokątnym układzie współrzędnych umieszczone są dwa przystające trójkąty oraz prosta 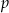 tak, jak na rysunku.
tak, jak na rysunku.
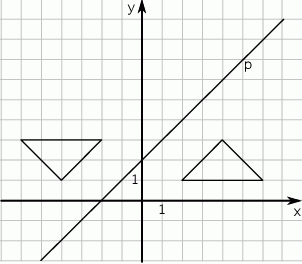
Jeden trójkąt jest symetryczny do drugiego względem
A) osi 
B) prostej 
C) punktu 
D) punktu przecięcia prostej 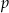 i osi
i osi 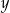 .
.
E) początku układu współrzędnych.
W prostokątnym układzie współrzędnych umieszczone są dwa przystające trójkąty oraz prosta  tak, jak na rysunku.
tak, jak na rysunku.
Jeden trójkąt jest symetryczny do drugiego względem
A) osi  B) prostej
B) prostej 
C) punktu 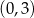 D) punktu przecięcia prostej
D) punktu przecięcia prostej  i osi
i osi 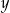 .
.
Każdy bok kwadratu  podzielono na 3 równe części i połączono kolejno punkty podziału, w wyniku czego otrzymano ośmiokąt (rysunek).
podzielono na 3 równe części i połączono kolejno punkty podziału, w wyniku czego otrzymano ośmiokąt (rysunek).
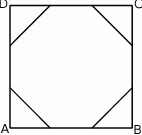
Które z poniższych zdań jest prawdziwe?
A) Ośmiokąt jest foremny.
B) Wszystkie boki ośmiokąta mają taką samą długość.
C) Każdy kąt wewnętrzny ośmiokąta ma miarę 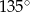 .
.
D) Obwód ośmiokąta jest większy od obwodu kwadratu 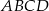 .
.
W zeszycie w linie narysowano dwa równoległoboki i trójkąt w sposób pokazany na rysunku. Odległości między sąsiednimi liniami są jednakowe. Podstawy wszystkich tych figur mają taką samą długość. Pole równoległoboku  jest równe 4.
jest równe 4.
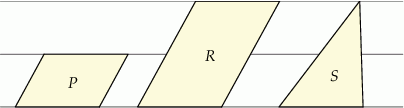
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Pole równoległoboku  jest równe 8. jest równe 8. | P | F |
Pole trójkąta  jest równe 4. jest równe 4. | P | F |
W zeszycie w linie narysowano dwa trójkąty i równoległobok w sposób pokazany na rysunku. Odległości między sąsiednimi liniami są jednakowe. Podstawy wszystkich tych figur mają taką samą długość. Pole trójkąta  jest równe 4.
jest równe 4.
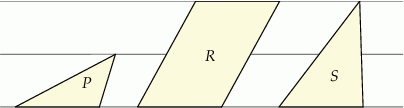
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Pole równoległoboku 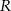 jest równe 12. jest równe 12. | P | F |
Pole trójkąta 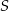 jest równe 8. jest równe 8. | P | F |
W beczce było 200 litrów wody, ale zaczęła ona wyciekać z szybkością 3 litrów na minutę. Zależność ilości wody w beczce (w litrach) od czasu (w minutach) przedstawia wzór
A) 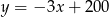 B)
B) 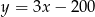 C)
C) 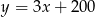 D)
D) 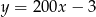
W zbiorniku było 1000 litrów wody, ale zaczęła ona wyciekać z szybkością 4 litrów na minutę. Zależność ilości wody w zbiorniku (w litrach) od czasu (w minutach) przedstawia wzór
A) 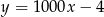 B)
B) 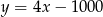 C)
C) 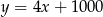 D)
D)