Promień okręgu opisanego na prostokącie o bokach: 6 cm i 8 cm jest równy:
A) 7 cm B) 6,5 cm C) 5 cm D) 10 cm
/Szkoła podstawowa/Zadania testowe
Na której osi liczbowej prawidłowo zaznaczono liczby 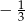 i
i 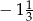 ?
?
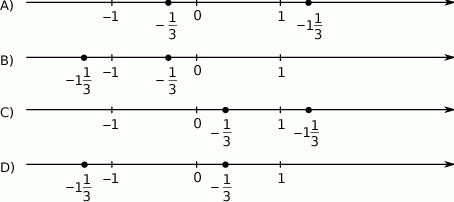
Tabela przedstawia funkcję określoną jednym z poniższych wzorów. Którym?
 | 1 | 2 | 3 | 4 |
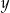 | 0 | 4 | 8 | 12 |
A) 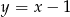 B)
B) 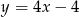 C)
C) 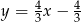 D)
D) 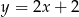
Tabela przedstawia funkcję określoną jednym z poniższych wzorów. Którym?
 | 1 | 2 | 3 | 4 |
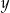 | 0 | 1 | 2 | 3 |
A) 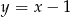 B)
B) 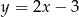 C)
C) 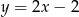 D)
D) 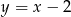
Tabela przedstawia funkcję określoną jednym z poniższych wzorów. Którym?
 | 1 | 2 | 3 | 4 |
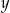 | 4 | 7 | 10 | 13 |
A) 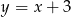 B)
B) 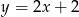 C)
C) 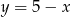 D)
D) 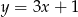
Jabłka i gruszki pakowano do pojemników, przy czym do jednego pojemnika wkładano 64 gruszki lub 80 jabłek. Po zapakowaniu owoców okazało się, że zapakowano dokładnie tyle samo jabłek, co gruszek.
Jaka jest najmniejsza możliwa liczba pojemników, do których zapakowano te owoce?
A) 5 B) 18 C) 9 D) 4
Jeśli długość jednego boku prostokąta zwiększymy o 20%, a długość drugiego boku prostokąta zmniejszymy o 5%, to pole prostokąta zwiększy się o:
A) 12% B) 14% C) 15% D) 16%
Jeśli długość jednego boku prostokąta zmniejszymy o 20%, a długość drugiego boku prostokąta zwiększymy o 5%, to pole prostokąta zmniejszy się o:
A) 12% B) 14% C) 15% D) 16%
Jeżeli odcinek 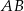 przecina oś
przecina oś 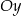 układu współrzędnych, to końce tego odcinka mogą mieć współrzędne
układu współrzędnych, to końce tego odcinka mogą mieć współrzędne
A) 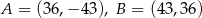 B)
B) 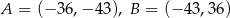
C) 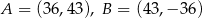 D)
D) 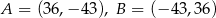
Na rysunku przedstawiono wykres pewnej funkcji.
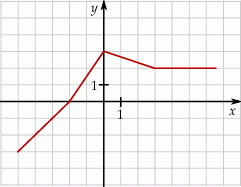
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Funkcja przyjmuje wartość 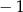 dla argumentu dla argumentu 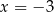 . . | P | F |
Dla wszystkich argumentów 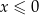 funkcja przyjmuje wartości ujemne. funkcja przyjmuje wartości ujemne. | P | F |
Na rysunku przedstawiono wykres pewnej funkcji.
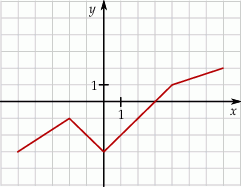
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Funkcja przyjmuje wartość 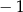 dla argumentu dla argumentu 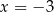 . . | P | F |
Dla wszystkich argumentów 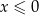 funkcja przyjmuje wartości ujemne. funkcja przyjmuje wartości ujemne. | P | F |
Na rysunku przedstawiono wykres pewnej funkcji.
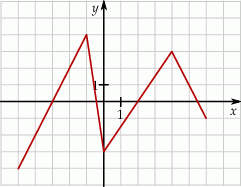
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Funkcja przyjmuje wartość 3 dla 4 argumentów. | P | F |
Dla wszystkich argumentów 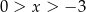 funkcja przyjmuje wartości dodatnie. funkcja przyjmuje wartości dodatnie. | P | F |
Napój otrzymano, po tym jak rozcieńczono 450 ml soku wodą w stosunku 1 : 10. Ile napoju otrzymano?
A) Więcej niż 4 litry, ale mniej niż 4,5 litra.
B) Dokładnie 4,5 litra.
C) Więcej niż 4,5 litra, ale mniej niż 5 litrów.
D) Dokładnie 5 litrów.
E) Więcej niż 5 litrów.
Na rysunku przedstawiono sześciokąt foremny o boku równym 2 cm. Przekątna 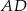 dzieli go na dwa przystające trapezy równoramienne.
dzieli go na dwa przystające trapezy równoramienne.
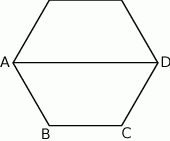
Wysokość trapezu 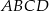 jest równa
jest równa
A) 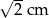 B)
B) 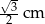 C)
C) 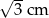 D) 2 cm
D) 2 cm
Na rysunku przedstawiono sześciokąt foremny  o boku równym 1 cm.
o boku równym 1 cm.
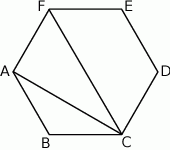
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Przekątna 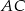 ma długość ma długość 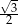 . . | P | F |
Przekątna 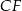 ma długość ma długość 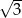 . . | P | F |
Na rysunku przedstawiono sześciokąt foremny o boku równym 4 cm. Przekątna 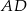 dzieli go na dwa przystające trapezy równoramienne.
dzieli go na dwa przystające trapezy równoramienne.
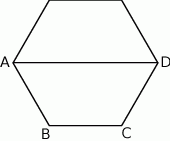
Pole trapezu 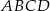 jest równe
jest równe
A) 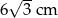 B)
B) 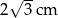 C)
C) 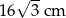 D)
D) 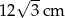
Na rysunku przedstawiono graniastosłup prosty i jego wymiary.
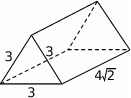
Objętość tego graniastosłupa jest równa
A) 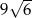 B)
B) 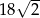 C)
C) 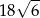 D)
D) 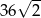
Na rysunku przedstawiono graniastosłup prosty i jego wymiary.
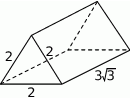
Objętość tego graniastosłupa jest równa
A)  B) 9 C)
B) 9 C) 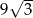 D)
D) 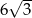
Na rysunku przedstawiono graniastosłup prosty i jego wymiary.
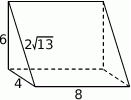
Objętość tego graniastosłupa jest równa
A) 48 B) 96 C) 32 D) 64
Łukasz wyciął z kartki papieru trójkąt równoramienny 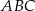 , a następnie zagiął w nim dwa narożniki tak, że wierzchołki
, a następnie zagiął w nim dwa narożniki tak, że wierzchołki 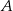 i
i 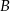 trójkąta znalazły się w środku
trójkąta znalazły się w środku 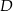 jego podstawy. Powstał w ten sposób pięciokąt
jego podstawy. Powstał w ten sposób pięciokąt 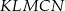 .
.
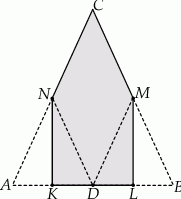
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Pole pięciokąta 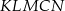 stanowi 75% pola trójkąta stanowi 75% pola trójkąta 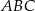 . . | P | F |
Obwód pięciokąta 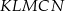 jest taki sam jak obwód trójkąta jest taki sam jak obwód trójkąta 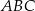 . . | P | F |
Z kwadratu odcięto trójkąty tak, że linie cięcia przeprowadzono przez środki boków tego kwadratu (rysunek I). Z odciętych trójkątów ułożono trójkąt  (rysunek II).
(rysunek II).
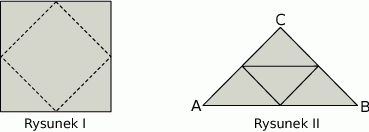
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Trójkąt  jest prostokątny i równoramienny. jest prostokątny i równoramienny. | P | F |
Pole trójkąta  jest połową pola kwadratu. jest połową pola kwadratu. | P | F |
Trójkąt równoboczny rozcięto na 16 przystających trójkątów (rysunek I). Z otrzymanych trójkątów ułożono dwa sześciokąty i mniejszy trójkąt równoboczny (rysunek II).
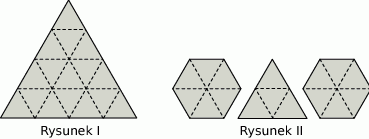
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Obwód dużego trójkąta z rysunku I jest równy sumie obwodów figur na rysunku II. | P | F |
| Suma pól sześciokątów z rysunku II stanowi 75% pola dużego trójkąta z rysunku I. | P | F |
Różnica 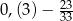 jest równa
jest równa
A) 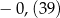 B)
B) 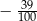 C)
C) 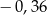 D)
D) 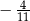
Różnica 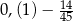 jest równa
jest równa
A) 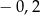 B)
B) 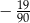 C)
C) 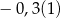 D)
D) 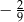
W tabeli przedstawiono informacje dotyczące cen akcji trzech firm w dwóch różnych wybranych dniach tego samego roku.
| Firma | Cena 1 akcji w dniu 1 lutego | Cena 1 akcji w dniu 31 sierpnia |
| Salceson S.A. | 15 zł | 18 zł |
| Kabanos S.A. | 24 zł | 36 zł |
| Salami S.A. | 96 zł | 64 zł |
A) 36 B) 18 C) 58 D) 40
W tabeli przedstawiono informacje dotyczące cen akcji trzech firm w dwóch różnych wybranych dniach tego samego roku.
| Firma | Cena 1 akcji w dniu 1 lutego | Cena 1 akcji w dniu 31 sierpnia |
| Salceson S.A. | 15 zł | 18 zł |
| Kabanos S.A. | 24 zł | 36 zł |
| Salami S.A. | 96 zł | 64 zł |
A) 40% B) 50%
[SQREMOVE]Wartość 60 akcji firmy Salceson S.A. i 10 akcji firmy Salami S.A. w okresie od między 1 lutego a 31 sierpnia C/D.
C) zmalała D) wzrosła
W tabeli przedstawiono informacje dotyczące cen akcji trzech firm w dwóch różnych wybranych dniach tego samego roku.
| Firma | Cena 1 akcji w dniu 1 lutego | Cena 1 akcji w dniu 31 sierpnia |
| Salceson S.A. | 15 zł | 18 zł |
| Kabanos S.A. | 24 zł | 36 zł |
| Salami S.A. | 96 zł | 64 zł |
| W okresie między 1 lutego a 31 sierpnia procentowy wzrost ceny akcji firmy Salceson S.A. by wyższy niż procentowy wzrost ceny akcji firmy Kabanos S.A. | P | F |
| Łączna wartość 40 akcji firmy Kabanos S.A. i 10 akcji firmy Salami S.A. była wyższa w dniu 31 sierpnia niż 1 lutego. | P | F |
Dane jest przybliżenie 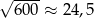 . Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
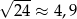 | P | F |
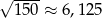 | P | F |
Dane jest przybliżenie 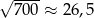 . Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
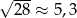 | P | F |
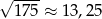 | P | F |
Na planie miasta, narysowanym w skali 1:20 000, park jest prostokątem o bokach 2 cm i 5 cm. Stąd wynika, że ten park ma powierzchnię
A) 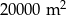 B)
B) 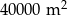 C)
C) 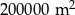 D)
D) 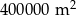
Na planie miasta, narysowanym w skali 1:25 000, park jest prostokątem o bokach 2 cm i 4 cm. Stąd wynika, że ten park ma powierzchnię
A) 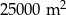 B)
B) 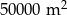 C)
C) 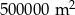 D)
D) 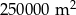
Punkty 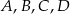 leżą na okręgu o środku w punkcie
leżą na okręgu o środku w punkcie 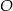 . Kąt środkowy
. Kąt środkowy 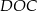 ma miarę
ma miarę 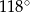 (zobacz rysunek).
(zobacz rysunek).
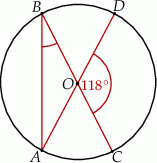
Miara kąta 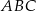 jest równa
jest równa
A) 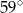 B)
B) 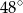 C)
C) 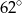 D)
D) 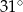
Punkty 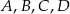 leżą na okręgu o środku w punkcie
leżą na okręgu o środku w punkcie 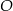 . Kąt środkowy
. Kąt środkowy 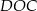 ma miarę
ma miarę 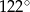 (zobacz rysunek).
(zobacz rysunek).
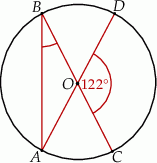
Miara kąta 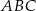 jest równa
jest równa
A) 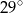 B)
B) 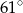 C)
C) 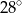 D)
D) 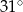
Na rysunku przedstawiono graniastosłup 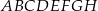 i ostrosłup
i ostrosłup 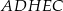 .
.
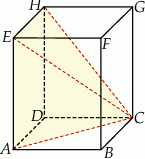
Objętość graniastosłupa jest większa od objętości ostrosłupa o 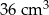 . Objętość ostrosłupa
. Objętość ostrosłupa 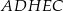 jest równa A/B.
jest równa A/B.
A) 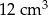 B)
B) 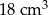
Objętość graniastosłupa 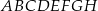 jest równa C/D.
jest równa C/D.
C) 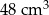 D)
D) 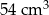
Na rysunku przedstawiono prostokąt 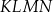 o bokach długości 24 cm i 10 cm.
o bokach długości 24 cm i 10 cm.

Czy wewnątrz tego prostokąta można umieścić odcinek 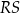 o długości
o długości 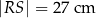 ? Wybierz odpowiedź T albo N i jej uzasadnienie spośród A, B albo C.
? Wybierz odpowiedź T albo N i jej uzasadnienie spośród A, B albo C.
| Tak | Nie |
| ponieważ | |
| A) | długość odcinka 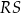 jest większa od długości odcinka jest większa od długości odcinka 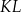 i większa od długości odcinka i większa od długości odcinka 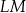 . . |
| B) | suma kwadratów długości odcinków 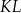 i i 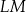 jest mniejsza niż kwadrat długości odcinka jest mniejsza niż kwadrat długości odcinka 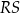 . . |
| C) | suma długości odcinków 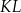 i i 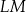 jest większa od długości odcinka jest większa od długości odcinka 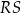 . . |
Na rysunku przedstawiono siatkę nietypowej sześciennej kostki do gry. Rzucamy jeden raz taką kostką.
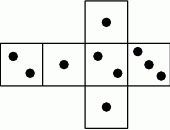
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Prawdopodobieństwo wyrzucenia nieparzystej liczby oczek jest 2 razy większe niż prawdopodobieństwo wyrzucenia parzystej liczby oczek. | P | F |
Prawdopodobieństwo wyrzucenia liczby oczek mniejszej od 3 jest równe  . . | P | F |
Na rysunku przedstawiono siatkę nietypowej sześciennej kostki do gry. Rzucamy jeden raz taką kostką.

Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Prawdopodobieństwo wyrzucenia nieparzystej liczby oczek jest 2 razy większe niż prawdopodobieństwo wyrzucenia parzystej liczby oczek. | P | F |
Prawdopodobieństwo wyrzucenia liczby oczek mniejszej od 3 jest równe  . . | P | F |
Na rysunku przedstawiono siatkę nietypowej ośmiościennej kostki do gry. Rzucamy jeden raz taką kostką.
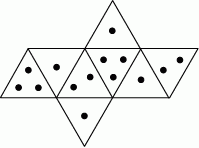
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Prawdopodobieństwo wyrzucenia nieparzystej liczby oczek jest 3 razy większe niż prawdopodobieństwo wyrzucenia parzystej liczby oczek. | P | F |
Prawdopodobieństwo wyrzucenia liczby oczek większej od 1 jest równe 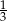 . . | P | F |
Na rysunku przedstawiono siatkę nietypowej dwunastościennej kostki do gry. Rzucamy jeden raz taką kostką.
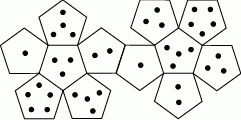
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Prawdopodobieństwo wyrzucenia nieparzystej liczby oczek jest większe niż prawdopodobieństwo wyrzucenia parzystej liczby oczek. | P | F |
Prawdopodobieństwo wyrzucenia liczby oczek większej od 3 jest mniejsze od 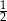 . . | P | F |
Dany jest prostokąt o wymiarach 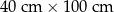 . Jeżeli każdy z dłuższych boków tego prostokąta wydłużymy o 20%, a każdy z krótszych boków skrócimy o 20%, to w wyniku obu przekształceń pole tego prostokąta
. Jeżeli każdy z dłuższych boków tego prostokąta wydłużymy o 20%, a każdy z krótszych boków skrócimy o 20%, to w wyniku obu przekształceń pole tego prostokąta
A) zwiększy się o 8% B) zwiększy się o 4%
C) zmniejszy się o 8% D) zmniejszy się o 4%
Dany jest prostokąt o wymiarach 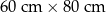 . Jeżeli każdy z dłuższych boków tego prostokąta wydłużymy o 10%, a każdy z krótszych boków skrócimy o 10%, to w wyniku obu przekształceń pole tego prostokąta
. Jeżeli każdy z dłuższych boków tego prostokąta wydłużymy o 10%, a każdy z krótszych boków skrócimy o 10%, to w wyniku obu przekształceń pole tego prostokąta
A) zwiększy się o 2% B) zwiększy się o 1%
C) zmniejszy się o 1% D) zmniejszy się o 2%

