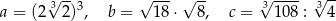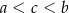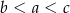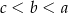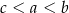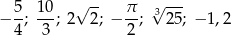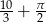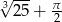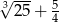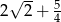Każdy bok pięciokąta foremnego 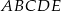 podzielono na 3 równe części i połączono kolejno punkty podziału, w wyniku czego otrzymano dziesięciokąt (rysunek).
podzielono na 3 równe części i połączono kolejno punkty podziału, w wyniku czego otrzymano dziesięciokąt (rysunek).
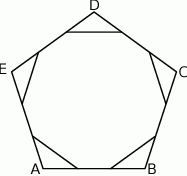
Które z poniższych zdań jest prawdziwe?
A) Dziesięciokąt jest foremny.
B) Wszystkie boki dziesięciokąta mają taką samą długość.
C) Każdy kąt wewnętrzny dziesięciokąta ma miarę 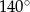 .
.
D) Obwód dziesięciokąta jest mniejszy od obwodu pięciokąta 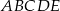 .
.

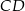 trójkąta równobocznego
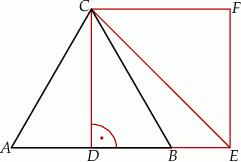
trójkąta równobocznego 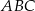 o boku długości 4 zbudowano kwadrat
o boku długości 4 zbudowano kwadrat  .
. 
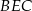 jest równe
jest równe 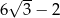
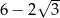
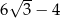
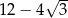
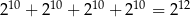
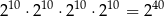
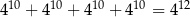
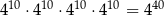
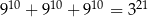
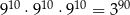
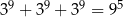
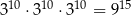
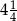 . Mniejsza z tych liczb jest równa
. Mniejsza z tych liczb jest równa 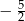 . Większa z tych liczb jest równa
. Większa z tych liczb jest równa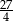

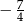
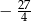
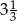 . Mniejsza z tych liczb jest równa
. Mniejsza z tych liczb jest równa 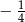 . Większa z tych liczb jest równa
. Większa z tych liczb jest równa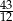
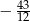
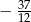
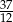
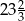 . Jeżeli mniejsza z tych liczb jest równa
. Jeżeli mniejsza z tych liczb jest równa 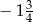 , to większa z tych liczb jest równa
, to większa z tych liczb jest równa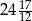
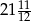
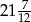
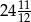
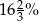
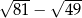 jest równe A/B.
jest równe A/B.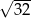
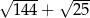 jest równe C/D.
jest równe C/D.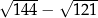 jest równe A/B.
jest równe A/B.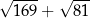 jest równe C/D.
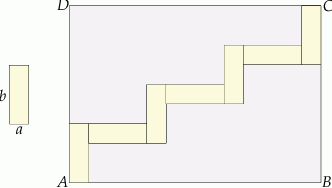
jest równe C/D.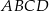 . Wzór ten składa się z 7 prostokątów o bokach
. Wzór ten składa się z 7 prostokątów o bokach  i
i 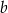 .
. 
 jest równe
jest równe 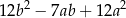
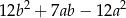
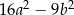
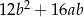
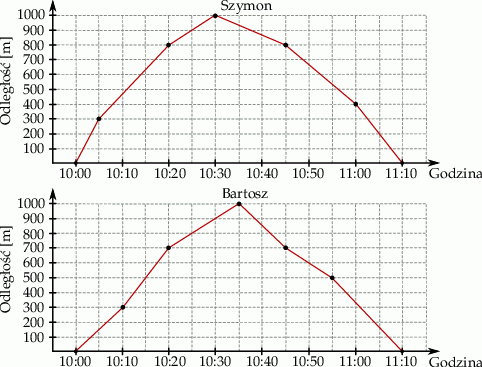
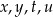 zapisane za pomocą wyrażeń arytmetycznych:
zapisane za pomocą wyrażeń arytmetycznych: 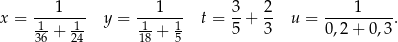

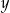
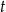

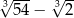 jest równa
jest równa 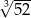
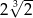
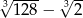 jest równa
jest równa 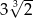
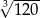
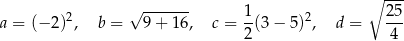
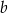 jest większa niż liczba
jest większa niż liczba  .
.  jest dwa razy mniejsza niż liczba
jest dwa razy mniejsza niż liczba  .
. 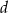 jest 2 razy mniejsza niż liczba
jest 2 razy mniejsza niż liczba 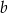 .
.  jest większa niż liczba
jest większa niż liczba 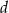 .
. 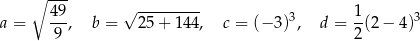
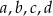 są dokładnie dwie liczby ujemne.
są dokładnie dwie liczby ujemne.  jest większa niż liczba
jest większa niż liczba  .
. 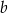 jest o 21 większa od liczby
jest o 21 większa od liczby 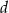 .
. 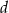 jest o 23 większa od liczby
jest o 23 większa od liczby  .
. 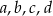 jest liczba, która nie jest liczbą całkowitą.
jest liczba, która nie jest liczbą całkowitą. 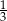
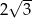
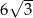
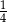
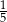
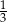
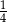
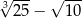 jest liczbą dodatnią.
jest liczbą dodatnią.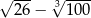 jest liczbą ujemną.
jest liczbą ujemną.