W pewnym zakładzie pracy każdy z pracowników codziennie montuje taką samą liczbę jednakowych podzespołów. Pracownicy potrzebowali 12 dni roboczych, aby wykonać zamówienie. Gdyby wydajność każdego z pracowników była wyższa o 20%, to wykonaliby zamówienie w
A) 8 dni B) 9 dni C) 10 dni D) 11 dni
/Szkoła podstawowa/Zadania testowe
Liczbą podzielną przez 36 jest
A) 345222 B) 986472 C) 322144 D) 631422
Z urny, w której jest wyłącznie 18 kul białych i 12 kul czarnych, losujemy 1 kulę.
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Prawdopodobieństwo wylosowania kuli białej jest równe 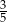 . . | P | F |
Prawdopodobieństwo wylosowania kuli czarnej jest mniejsze od 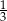 | P | F |
Z urny, w której jest wyłącznie 16 kul białych i 24 kule czarne, losujemy 1 kulę.
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Prawdopodobieństwo wylosowania kuli białej jest równe  . . | P | F |
Prawdopodobieństwo wylosowania kuli czarnej jest większe od  | P | F |
Para liczb 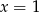 i
i 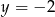 jest rozwiązaniem układu równań
jest rozwiązaniem układu równań
A) 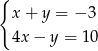 B)
B) 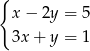 C)
C) 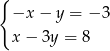 D)
D) 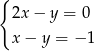
Para liczb 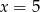 i
i 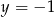 jest rozwiązaniem układu równań
jest rozwiązaniem układu równań
A) 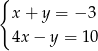 B)
B) 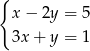 C)
C) 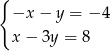 D)
D) 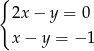
Para liczb 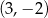 spełnia układ równań
spełnia układ równań
A) 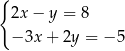 B)
B) 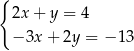
C) 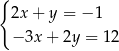 D)
D) 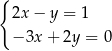
Para liczb 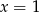 i
i 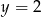 jest rozwiązaniem układu równań
jest rozwiązaniem układu równań
A) 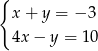 B)
B) 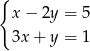 C)
C) 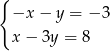 D)
D) 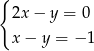
Para liczb 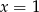 i
i 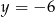 jest rozwiązaniem układu równań
jest rozwiązaniem układu równań
A) 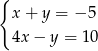 B)
B) 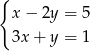 C)
C) 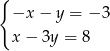 D)
D) 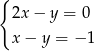
W dodatniej liczbie trzycyfrowej cyfra dziesiątek jest równa 5, a cyfra setek jest o 6 mniejsza od cyfry jedności. Ile jest liczb spełniających te warunki?
A) Jedna. B) Dwie. C) Trzy. D) Cztery.
W dodatniej liczbie trzycyfrowej cyfra dziesiątek jest równa 7, a cyfra setek jest o 6 większa od cyfry jedności. Ile jest liczb spełniających te warunki?
A) Jedna. B) Dwie. C) Trzy. D) Cztery.
Ile spośród liczb: 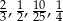 spełnia warunek
spełnia warunek 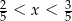 ?
?
A) Jedna liczba. B) Dwie liczby. C) Trzy liczby. D) Cztery liczby.
Ile spośród liczb: 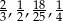 spełnia warunek
spełnia warunek 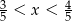 ?
?
A) Jedna liczba. B) Dwie liczby. C) Trzy liczby. D) Cztery liczby.
W układzie współrzędnych narysowano wykres funkcji i zaznaczono jego punkty przecięcia z prostą 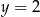 .
.
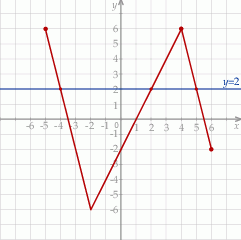
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Funkcja przyjmuje wartość 2 dla pewnego argumentu będącego liczbą nieparzystą. | P | F |
Dla wszystkich argumentów większych od 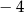 i jednocześnie mniejszych od 4 funkcja przyjmuje wartości mniejsze niż 2. i jednocześnie mniejszych od 4 funkcja przyjmuje wartości mniejsze niż 2. | P | F |
Na którym rysunku narysowana prosta jest osią symetrii figury?
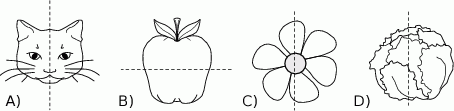
Na krótszym boku prostokąta zbudowano trójkąt równoboczny o obwodzie 18 cm, a na dłuższym boku prostokąta zbudowano kwadrat o polu równym 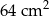 . Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Pole prostokąta jest o 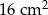 mniejsze od pola kwadratu powstałego na dłuższym boku prostokąta. mniejsze od pola kwadratu powstałego na dłuższym boku prostokąta. | P | F |
| Obwód prostokąta jest o 10 cm dłuższy od obwodu trójkąta równobocznego zbudowanego na krótszym boku prostokąta. | P | F |
Na krótszym boku prostokąta zbudowano sześciokąt foremny o obwodzie 42 cm, a na dłuższym boku zbudowano pięciokąt foremny o obwodzie 55 cm. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Pole prostokąta jest równe 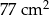 . . | P | F |
| Obwód prostokąta jest o 8 cm krótszy od obwodu sześciokąta foremnego zbudowanego na krótszym boku prostokąta. | P | F |
Na dłuższym boku prostokąta zbudowano trójkąt równoboczny o obwodzie 24 cm, a na krótszym boku prostokąta zbudowano kwadrat o polu równym 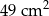 . Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Obwód prostokąta jest o 6 cm dłuższy od obwodu trójkąta równobocznego zbudowanego na dłuższym boku prostokąta. | P | F |
Pole prostokąta jest o 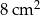 większe od pola kwadratu powstałego na krótszym boku prostokąta. większe od pola kwadratu powstałego na krótszym boku prostokąta. | P | F |
Dany jest wzór opisujący pole trójkąta 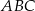 :
: 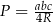 , gdzie
, gdzie 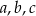 są długościami boków tego trójkąta, a
są długościami boków tego trójkąta, a 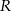 jest promieniem okręgu przechodzącego przez punkty
jest promieniem okręgu przechodzącego przez punkty 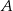 ,
, 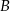 i
i 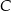 . Promień
. Promień 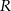 można wyrazić wzorem A/B.
można wyrazić wzorem A/B.
A) 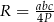 B)
B) 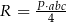
Długość boku  trójkąta
trójkąta 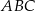 można wyrazić wzorem C/D.
można wyrazić wzorem C/D.
C) 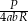 D)
D) 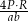
Suma dwóch dodatnich liczb  i
i 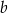 jest równa 46. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
jest równa 46. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Po zmniejszeniu każdej z tych liczb o 6 suma otrzymanych liczb będzie równa 34. | P | F |
| Po zwiększeniu każdej z tych liczb o połowę suma otrzymanych liczb będzie równa 69. | P | F |
Różnica dwóch dodatnich liczb  i
i 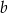 jest równa 76. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
jest równa 76. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Po zmniejszeniu każdej z tych liczb o 6 różnica otrzymanych liczb będzie równa 64. | P | F |
| Po zwiększeniu każdej z tych liczb o połowę różnica otrzymanych liczb będzie równa 114. | P | F |
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Jeżeli liczba dzieli się przez 144 i 96, to dzieli się też przez 576. | P | F |
| Jeżeli liczba jest dzielnikiem 144 i 96, to liczba ta jest dzielnikiem 48. | P | F |
Ze zbioru liczb naturalnych dwucyfrowych losujemy jedną liczbę. Jakie jest prawdopodobieństwo, że w zapisie dziesiętnym wylosowanej liczby jest dokładnie jedna cyfra 3?
A) 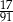 B)
B) 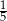 C)
C) 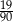 D)
D) 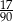
Spośród wszystkich liczb dwucyfrowych dodatnich losujemy jedną liczbę. Prawdopodobieństwo wylosowania liczby podzielnej przez 20 jest równe
A) 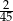 B)
B) 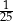 C)
C) 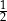 D)
D) 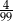
W trójkącie 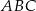 poprowadzono wysokości
poprowadzono wysokości 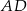 i
i 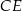 . Odcinek
. Odcinek 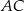 ma taką samą długość
ma taką samą długość 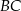 , a kąt
, a kąt 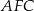 ma miarę
ma miarę 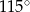 (zobacz rysunek).
(zobacz rysunek).
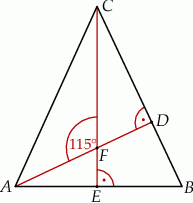
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Trójkąt 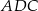 jest równoramienny. jest równoramienny. | P | F |
Kąt 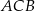 ma miarę ma miarę 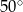 . . | P | F |
Pole ćwiartki koła przedstawionej na rysunku jest równe 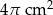 .
.
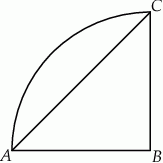
Pole trójkąta 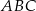 jest równe
jest równe
A) 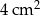 B)
B) 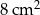 C)
C) 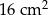 D)
D) 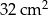
Do pomalowania wszystkich ścian graniastosłupa czworokątnego zużyto 30 mililitrów farby o wydajności 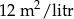 .
.
Pole powierzchni tego graniastosłupa jest równe
A) 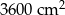 B)
B) 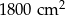 C)
C) 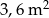 D)
D) 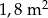
Dane są liczby 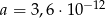 oraz
oraz 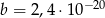 . Wtedy iloraz
. Wtedy iloraz 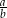 jest równy
jest równy
A) 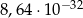 B)
B) 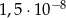 C)
C) 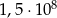 D)
D) 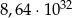
Dane są liczby 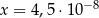 oraz
oraz 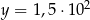 . Wtedy iloraz
. Wtedy iloraz 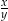 jest równy
jest równy
A) 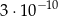 B)
B) 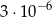 C)
C) 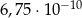 D)
D) 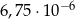
Dane są liczby 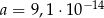 oraz
oraz 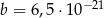 . Wtedy iloraz
. Wtedy iloraz 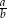 jest równy
jest równy
A) 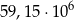 B)
B) 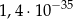 C)
C) 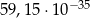 D)
D) 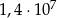
Dane są liczby 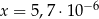 oraz
oraz 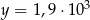 . Wtedy iloraz
. Wtedy iloraz 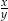 jest równy
jest równy
A) 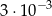 B)
B) 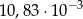 C)
C) 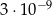 D)
D) 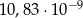
Długość jednego boku kwadratu 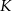 skrócono o 20%, a długość drugiego boku skrócono o 40%. W wyniku tych operacji otrzymano prostokąt
skrócono o 20%, a długość drugiego boku skrócono o 40%. W wyniku tych operacji otrzymano prostokąt 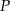 . Stosunek długości przekątnej kwadratu
. Stosunek długości przekątnej kwadratu 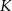 do długości przekątnej prostokąta
do długości przekątnej prostokąta 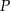 jest równy
jest równy
A) 0,48 B) 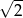 C) 1 D) 2
C) 1 D) 2
Wypisano ułamki spełniające łącznie następujące warunki:
-
mianownik każdego z nich jest równy 4,
-
licznik każdego z nich jest liczbą naturalną większą od mianownika,
-
każdy z tych ułamków jest większy od liczby 3 oraz mniejszy od liczby 5.
Wszystkich ułamków spełniających powyższe warunki jest
A) sześć B) siedem C) osiem D) dziewięć
W pewnym rombie jeden z kątów wewnętrznych ma miarę 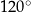 . Obwód tego rombu jest równy 24 cm. Dłuższa przekątna tego rombu ma długość
. Obwód tego rombu jest równy 24 cm. Dłuższa przekątna tego rombu ma długość
A) 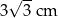 B) 6 cm C)
B) 6 cm C) 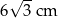 D) 12 cm
D) 12 cm
W pewnym rombie jeden z kątów wewnętrznych ma miarę 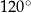 . Obwód tego rombu jest równy 28 cm. Dłuższa przekątna tego rombu ma długość
. Obwód tego rombu jest równy 28 cm. Dłuższa przekątna tego rombu ma długość
A) 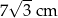 B) 7 cm C)
B) 7 cm C) 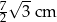 D) 14 cm
D) 14 cm

