Wykresem funkcji kwadratowej 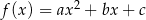 jest parabola styczna do prostej
jest parabola styczna do prostej 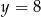 w punkcie
w punkcie 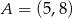 oraz przechodząca przez punkt
oraz przechodząca przez punkt 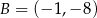 . Wyznacz wartości współczynników
. Wyznacz wartości współczynników 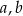 i
i  .
.
/Szkoła średnia/Funkcje/Kwadratowa/Wyznacz wzór
Jednym z miejsc zerowych funkcji kwadratowej 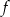 jest liczba 5, maksymalny przedział, w którym ta funkcja jest malejąca to
jest liczba 5, maksymalny przedział, w którym ta funkcja jest malejąca to 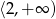 . Największa wartość funkcji
. Największa wartość funkcji 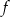 w przedziale
w przedziale 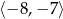 jest równa
jest równa 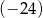 . Wyznacz wzór funkcji
. Wyznacz wzór funkcji 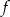 i narysuj jej wykres.
i narysuj jej wykres.
Zbiorem wartości funkcji kwadratowej 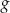 jest przedział
jest przedział 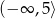 , a zbiorem rozwiązań nierówności
, a zbiorem rozwiązań nierówności 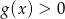 jest przedział
jest przedział 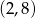 . Wyznacz wzór funkcji
. Wyznacz wzór funkcji 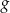 .
.
Napisz wzór i narysuj wykres funkcji 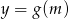 , która każdej liczbie rzeczywistej
, która każdej liczbie rzeczywistej 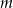 przyporządkowuje najmniejszą wartość funkcji kwadratowej
przyporządkowuje najmniejszą wartość funkcji kwadratowej 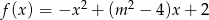 w przedziale
w przedziale 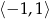 .
.
Do wykresu pewnej funkcji kwadratowej 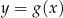 należy punkt o współrzędnych
należy punkt o współrzędnych 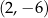 . Osią symetrii wykresu tej funkcji jest prosta o równaniu
. Osią symetrii wykresu tej funkcji jest prosta o równaniu 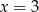 , a jednym z miejsc zerowych funkcji
, a jednym z miejsc zerowych funkcji 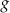 jest
jest 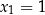 . Wyznacz wzór funkcji
. Wyznacz wzór funkcji 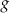 w postaci iloczynowej.
w postaci iloczynowej.
Funkcja kwadratowa 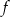 przyjmuje największą wartość równą
przyjmuje największą wartość równą 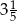 , a zbiorem rozwiązań nierówności
, a zbiorem rozwiązań nierówności 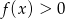 jest przedział
jest przedział 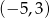 . Wyznacz wzór funkcji
. Wyznacz wzór funkcji 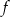 w postaci ogólnej.
w postaci ogólnej.
Funkcja kwadratowa 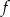 ma tylko jedno miejsce zerowe, przyjmuje największą wartość dla argumentu
ma tylko jedno miejsce zerowe, przyjmuje największą wartość dla argumentu 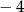 , a do jej wykresu należy punkt
, a do jej wykresu należy punkt 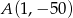 . Napisz wzór funkcji
. Napisz wzór funkcji 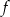 w postaci ogólnej.
w postaci ogólnej.
Funkcja kwadratowa 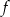 ma tylko jedno miejsce zerowe, przyjmuje największą wartość dla argumentu
ma tylko jedno miejsce zerowe, przyjmuje największą wartość dla argumentu 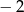 , a do jej wykresu należy punkt
, a do jej wykresu należy punkt 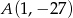 . Napisz wzór funkcji
. Napisz wzór funkcji 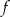 w postaci ogólnej.
w postaci ogólnej.
Funkcja kwadratowa 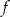 określona jest wzorem
określona jest wzorem 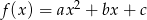 . Zbiorem rozwiązań nierówności
. Zbiorem rozwiązań nierówności 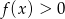 jest przedział
jest przedział 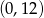 . Największa wartość funkcji
. Największa wartość funkcji 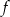 jest równa 9. Oblicz współczynniki
jest równa 9. Oblicz współczynniki  i
i  funkcji
funkcji 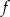 .
.
Funkcja kwadratowa 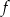 określona jest wzorem
określona jest wzorem 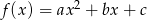 . Zbiorem rozwiązań nierówności
. Zbiorem rozwiązań nierówności 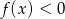 jest przedział
jest przedział 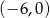 . Najmniejsza wartość funkcji
. Najmniejsza wartość funkcji 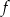 jest równa
jest równa 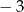 . Oblicz współczynniki
. Oblicz współczynniki 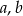 i
i  funkcji
funkcji 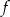 .
.
Liczby 1 i 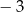 są miejscami zerowymi funkcji kwadratowej
są miejscami zerowymi funkcji kwadratowej 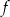 oraz do jej wykresu należy punkt
oraz do jej wykresu należy punkt 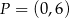 . Wyznacz wzór ogólny tej funkcji.
. Wyznacz wzór ogólny tej funkcji.
Liczby 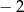 i
i 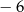 są miejscami zerowymi funkcji kwadratowej
są miejscami zerowymi funkcji kwadratowej 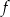 oraz do jej wykresu należy punkt
oraz do jej wykresu należy punkt 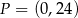 . Wyznacz wzór ogólny tej funkcji.
. Wyznacz wzór ogólny tej funkcji.
Jedynym miejscem zerowym funkcji kwadratowej 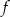 jest liczba 2. Wykres funkcji
jest liczba 2. Wykres funkcji 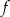 przecina oś
przecina oś 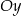 w punkcie o współrzędnych
w punkcie o współrzędnych 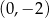 . Wyznacz wzór tej funkcji w postaci ogólnej.
. Wyznacz wzór tej funkcji w postaci ogólnej.
Funkcja kwadratowa 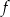 ma dokładnie jedno miejsce zerowe równe 2. Ponadto
ma dokładnie jedno miejsce zerowe równe 2. Ponadto 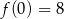 . Wyznacz wzór funkcji
. Wyznacz wzór funkcji 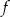 .
.
Wyznacz wzór ogólny funkcji kwadratowej, której największą wartością jest 2, a miejscami zerowymi są liczby 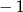 i 3.
i 3.
Wyznacz wzór ogólny funkcji kwadratowej, której najmniejszą wartością jest 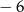 , a miejscami zerowymi są liczby
, a miejscami zerowymi są liczby 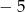 i 3.
i 3.
Funkcja kwadratowa 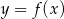 przyjmuje wartości ujemne tylko dla
przyjmuje wartości ujemne tylko dla 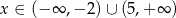 , a jej zbiorem wartości jest przedział
, a jej zbiorem wartości jest przedział 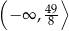 . Zapisz wzór funkcji kwadratowej
. Zapisz wzór funkcji kwadratowej 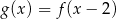 w postaci ogólnej.
w postaci ogólnej.
Funkcja kwadratowa 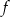 określona jest wzorem
określona jest wzorem 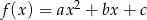 . Zbiorem rozwiązań nierówności
. Zbiorem rozwiązań nierówności 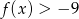 jest przedział
jest przedział 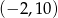 , a zbiorem rozwiązań nierówności
, a zbiorem rozwiązań nierówności 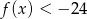 jest zbiór
jest zbiór 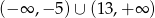 . Oblicz współczynniki
. Oblicz współczynniki 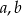 i
i  funkcji
funkcji 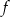 .
.
Funkcja kwadratowa 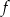 ma następujące własności:
ma następujące własności:
– zbiorem wartości funkcji 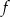 jest przedział
jest przedział 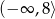 ;
;
– funkcja 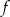 jest rosnąca w przedziale
jest rosnąca w przedziale 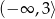 i malejąca w przedziale
i malejąca w przedziale 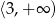 ;
;
– wykres funkcji 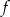 przecina oś
przecina oś 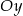 w punkcie, którego rzędna jest równa
w punkcie, którego rzędna jest równa 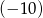 .
.
Wyznacz wzór funkcji 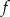 w postaci iloczynowej.
w postaci iloczynowej.

